浅埋隧道岩土体参数正交反演及衬砌工作状态评价

王迎超，尚岳全，徐兴华

(1. 中国矿业大学 深部岩土力学与地下工程国家重点实验室，江苏 徐州 221008；2. 浙江大学 建筑工程学院，浙江 杭州，310058)

在山岭隧道建设过程中，常常遇到破碎围岩段。公路隧道设计规范[1]规定，在Ⅳ～Ⅵ级围岩条件下，围岩自稳能力差，宜采用有仰拱的封闭式衬砌断面。破碎围岩段能否安全顺利施工，支护是关键。如果隧道支护结构设计不合理，易导致掉块、塌方等灾害事故，对现场施工人员构成生命威胁。因此，对隧道衬砌的工作状态进行合理评价，具有重要指导意义。根据隧道衬砌的受力情况可直接评价其工作状态。随着计算机技术的发展，通过建立合理的数值模型计算隧道衬砌结构的内力，是一种比较有效的方法。但是，有限元计算的精度往往受到所选取岩土体物理力学参数的影响，因此，如何选取合理的岩土参数是解决此类问题的关键。基于现场监控量测数据的位移反演分析方法的出现，很好地解决了这一隧道工程难题。反演分析方法主要可以分为2大类：一是逆反分析，即直接建立基本控制方程的逆方程，通过最小二乘解由量测位移反求待定参数，这种方法较直接，但建立逆反方程比较困难，所以应用不多；二是正分析法，其基本原理是通过转化，最终转变为一目标函数的寻优问题，然后运用各种优化技术来进行计算，如黄金分割法、单纯形法、复合形法、可变容差法等。但由于各种优化方法有其自身的局限性，往往使计算收敛缓慢或陷入局部极小值，不能得到满意的结果。许多学者尝试将各种非线性理论用于反演分析，如神经网络理论[2-5]、遗传算法[6-7]、扩张卡尔曼滤波法[8-9]、人工智能[10]、非线性最优化技术[11]等，取得一定的研究成果。但由于非线性理论计算过于繁琐，不利于现场推广应用，因此，还不能很好地服务于隧道工程建设。正交数值试验法很好地解决了以上问题，它是通过建立正交表，运用数值正交试验进行有限元计算，然后结合现场监控量测数据，最终得到较为合理的参数值。吕庆等[12-14]将该方法用于岩土工程反分析中，取得良好效果。目前隧道衬砌结构的设计是以工程类别法为主，理论验算为辅，其主要原因是衬砌所受荷载不易确定。国内许多学者进行了这方面的研究，主要集中在对围岩压力分布形式的反演[15-19]和对钢拱架受力的量测及有限元分析[20-22]2个方面，而对隧道衬砌结构工作状态评价研究还比较少。本文作者基于马鞍山隧道实测拱顶下沉和洞周收敛数据，根据正交设计思想，确立试验方案，结合弹塑性非线性有限元计算，反演岩土体的物理力学参数。然后，进行有限元正算分析，得到隧道衬砌结构的内力。最后，运用钢筋混凝土结构相关理论计算衬砌结构的设计内力，并定义安全度的概念来评价衬砌结构的工作状态，以便为浅埋隧道破碎围岩段衬砌结构的工作状态提供一种合理的评价思路。

1 岩土体物理力学参数的正交反演

1.1 正交试验原理

正交试验设计是研究多因素多水平的一种设计方法，它是根据正交性从全面试验中挑选出部分有代表性的点进行试验，这些有代表性的点具备“均匀分散，齐整可比”的特点。正交试验设计是分式析因设计的主要方法，是一种高效率、快速、经济的实验设计方法。日本田口玄一将正交试验选择的水平组合列成表格，称为正交表。

通过正交试验可以从多组参数组合中筛选出有代表性和典型性的组合，并进行优化计算后得到最佳参数组合，从而避免了直接反演法中大量的迭代和搜索工作。

1.2 反演参数选取

反分析方法按照采用的监控量测数据不同，可分为应力反分析、应变反分析和位移反分析等，目前应用最广泛的是位移反分析。在采用位移反演岩土体的物理力学参数时，从理论上讲，选取的反演参数越多，越能逼近实际情况。但待求参数过多，将使计算工作量大大增加，因此，应考虑各参数间的相互关系和影响，选取对隧道围岩系统产生重要影响而通过试验又不易确定的参数。

隧道围岩的主要物理力学参数有弹性模量 E、泊松比µ、内聚力c和内摩擦角φ。其中，岩土体的强度参数(内聚力c和内摩擦角φ)通过室内试验容易确定，弹性模量 E和泊松比 µ是影响位移场变化的重要参数，且现场不易获得，因此，这里将其作为反演参数进行分析。

1.3 反演步骤

(1) 通过正交设计试验安排反演参数的试算初始值。

(2) 依据直接逼近试凑的正算反分析法，将反分析问题转化为正演计算目标函数的寻优问题。

(3) 进行有限元计算。根据有限元计算结果和关键点的实测值，建立如下目标函数：

式中：ui为第i个测点的有限元计算值，mm，理论上它是反演参数向量的函数；为第i个测点的实测位移，mm；m为测点总数。

(4) 通过优化计算，找出使目标函数f(x)最小的参数组合，即为反演结果。

2 隧道衬砌工作状态评价

通过上述正交反演分析，可以得到较为准确的岩土体物理力学参数，进而通过有限元计算可以得到衬砌结构内力(弯矩、剪力和轴力)。隧道的支护结构属于钢筋混凝土结构，其受力状态相当复杂。这里为了更好地对衬砌进行合理评价，定义衬砌的安全度为：

式中：[F]为依据实际使用的配筋量，计算所得的衬砌所能承受的最大内力(弯矩、剪力和轴力)；F为通过有限元计算得到的衬砌内力；K为衬砌的安全度，K＞1，表示衬砌处于安全状态，有一定的安全余度；K=1，表示衬砌处于极限使用状态，应加强观察和监测；K＜1，表示衬砌处于危险状态，应采取相应的工程加固措施。

从安全角度考虑，在对衬砌进行状态评价时，应选取最危险断面进行分析。按照实际配筋，计算其所能承受的最大内力，即内力设计值。对于衬砌结构按照偏心受压构件处理，可分为大偏心受压破坏和小偏心受压破坏2种情况，按偏心受压对称配筋计算。

2.1 界限情况下受压承载力设计值的计算

截面的有效高度为：

式中：h0为截面的有效高度，mm；h为截面的高度，mm；as为受拉钢筋合力作用点到截面受拉边缘的距离，mm。

衬砌所能承受的最大轴力为：

式中：Nb为轴力设计值，kN；α1为受压区混凝土矩形应力图的应力与混凝土轴心抗压强度的比值；fc为混凝土轴心抗压强度，N/mm2；b为截面的宽度，mm；ξb为相对界限受压区高度；xb为界限受压区高度，mm，xb=ξbh0。

若 N≤Nb，则为大偏心受压；若 N＞Nb，则为小偏心受压。其中，N为通过有限元计算得到的衬砌的轴力，kN。

2.2 当判断为大偏心受压情况时受压承载力设计值的计算

图1所示为大偏心受压破坏的截面计算图形。根据截面应力图形(图1)，可以得到大偏心受压情况的基本方程为：

式中：x为受压区计算高度，当x＞h，取x=h，mm；e为轴心力作用点至受拉钢筋As合力点之间的距离，mm；fy为受拉区纵向钢筋的抗压强度设计值，N/mm2；f′y为受压区纵向钢筋的抗压强度设计值，N/mm2；As为受拉钢筋的截面面积，mm2；A′s为受压钢筋的截面面积，mm2；a′s为受压钢筋合力作用点到截面受拉边缘的距离，mm。

图1 大偏心受压破坏的截面计算图Fig.1 Calculation graphic of section under state of great eccentric compressive failure

因采用对称配筋，故由式(5)得：

由式(6)得：

轴心力作用点至受拉钢筋As合力点之间的距离e可表示为：

式中：ei为初始偏心距；η为偏心距增大系数。

偏心距增大系数为：

式中：l0为构件的计算长度，mm；ξ1为偏心受压构件的截面曲率修正系数，当ξ1＞1.0时，取ξ1=1.0；ξ2为构件长细比对截面曲率的影响系数，当l0/h＜15时，取 ξ2=1.0。

由式(9)可以计算出初始偏心距：

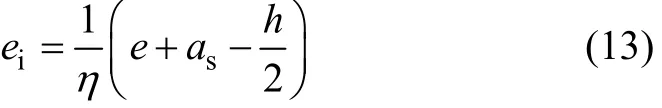
轴心力对截面重心的偏心距为：

式中：e0为轴向力对截面重心的偏心距，mm；ea为附

衬砌所能承受的最大弯矩Mmax为：

2.3 当判断为小偏心受压情况时受压承载力设计值计算

图2所示为小偏心受压破坏的截面计算图。根据图2可以得到小偏心受压情况的基本方程：

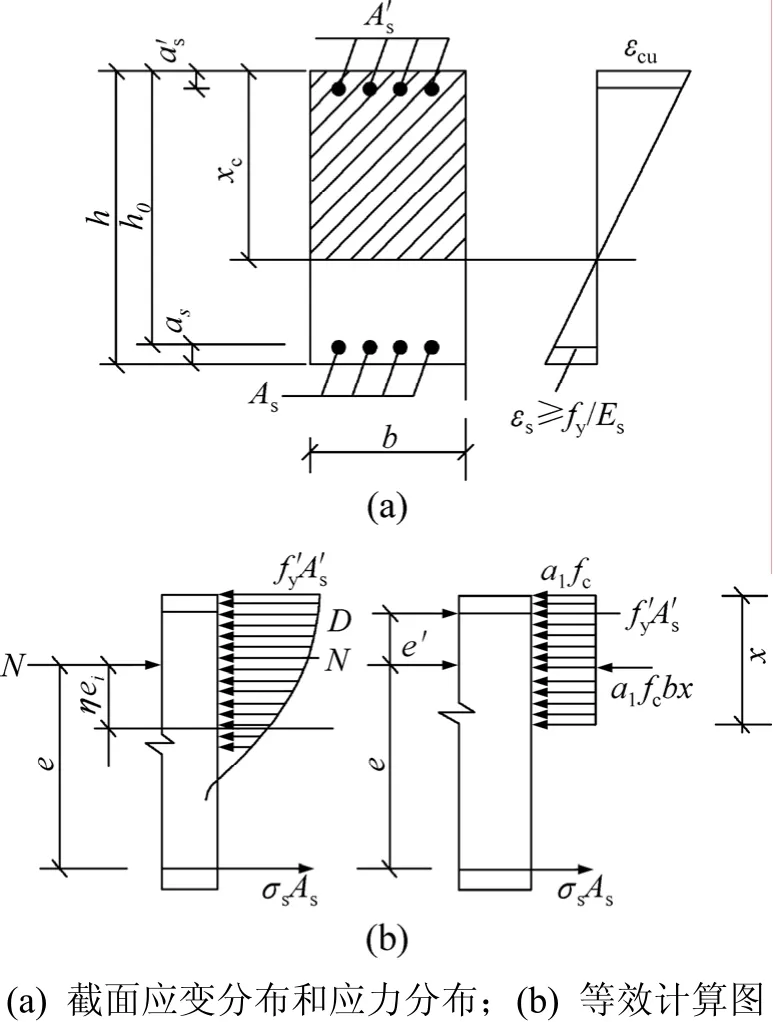
图2 小偏心受压破坏的截面计算图Fig.2 Calculation graphic of section under state of small eccentric compressive failure

式中：ξ为受压区的相对计算高度，ξ=x/h0。

由式(16)得到受压区的计算高度：

将式(18)代入式(17)中，可求得轴心力作用点至受拉钢筋As合力点之间的距离e，再根据式(9)～(15)即可得到衬砌所能承受的最大弯矩Mmax。

对于小偏心受压构件，还需进行平面外承载力验算，即要求

式中：Nb为轴向压力设计值，kN；φ为钢筋混凝土构件的稳定系数；fc为混凝土的轴心抗压强度设计值，N/mm2；A为构件的截面面积，mm2；sA′为全部纵向钢筋的截面面积，mm2。

3 工程实例分析

3.1 工程概况

马鞍山隧道位于浙江省诸(暨)永(嘉)高速公路金华段(东阳)第S107合同段，该隧道位于浙中中低山丘陵区，中间高，东西两端低，山顶海拔高为367.08 m，地形自然坡度为 30°～35°，植被发育。中低山丘陵区溪流狭窄、弯曲，树枝状水系相当发育，雨季溪水湍急，瀑涨瀑落，枯水期流量较小，部分干涸。隧道设计为单向行车双车道分离式隧道，施工图设计桩号为：K97+412～K97+594，长为182 m。隧道出洞口位于一斜坡上，坡体上覆盖约厚为10 m的第四系松散覆盖层和全风化凝灰岩，风化裂隙极发育，岩体破碎，呈角碎石状，结构松散。松散覆盖层以下为弱风化凝灰岩，设计围岩类别为Ⅳ级，坚硬、构造节理发育，节理裂隙面渲染铁锰质氧化膜。隧道跨度为12.7 m，开挖高度为10.3 m，衬砌断面为四心圆形式，使用带仰拱的封闭式断面，衬砌采用模筑钢筋混凝土结构。

3.2 现场监控量测

马鞍山隧道采用 2台阶法施工，布置 1个拱顶下沉量测点A和2条水平收敛测线BB′和CC′，监测断面布设如图3所示。在该隧道施工过程中，对左右洞室K97+547断面均进行了监控量测，各关键点实测位移如表1所示。

3.3 有限元计算模型建立

选取K97+547断面(埋深46 m)进行模拟计算，计算模型网格剖分如图4所示。模型左右边界距洞口的距离取为隧道宽度的7倍，隧道下方取为隧道洞径的5倍，上部取至地表。计算模型的边界条件除上部为自由边界外，其余侧面和底面均采用法向约束边界。

表1 马鞍山隧道K97+547拱顶下沉和水平收敛实测值Table 1 Measured convergence and subsidence of vault at K97+547 of Maanshan tunnel mm

图3 拱顶下沉和净空变形测线布设示意图Fig.3 Monitoring arrangement sketch of convergence and subsidence of vault

根据马鞍山隧道工程地质勘察报告，隧道上覆岩土层按两层考虑。其中，上层为全风化凝灰岩和第四系松散覆盖层厚，厚约10 m；此覆盖层以下为Ⅳ级围岩。采用平面4节点等参元模拟隧道围岩，隧道支护结构采用梁单元模拟，锚杆的作用通过提高加固区域围岩的物理力学参数模拟。采用弹塑性非线性有限元进行计算。隧道围岩和支护结构的物理力学参数如表2所示。

图4 有限元计算模型Fig.4 Finite element model

3.4 正交表设计

在反演分析计算过程中，共需反演松散覆盖层的弹性模量E1和泊松比µ1、基岩层的弹性模量 E2和泊松比µ24个参数。参照类似隧道工程经验确定每个参数的计算区间，每个参数取5个水平，确定的影响因素水平表如表3所示。本次正交试验的次数为52=25次，选用L25(54)正交表，其下标25表示共要做25次试验，括号内的5表示每个因素的水平数为5，上标4表示该正交表中共有4个因素。

表2 围岩与支护结构的物理力学性能Table 2 Physico-mechanical properties of surrounding rock and lining

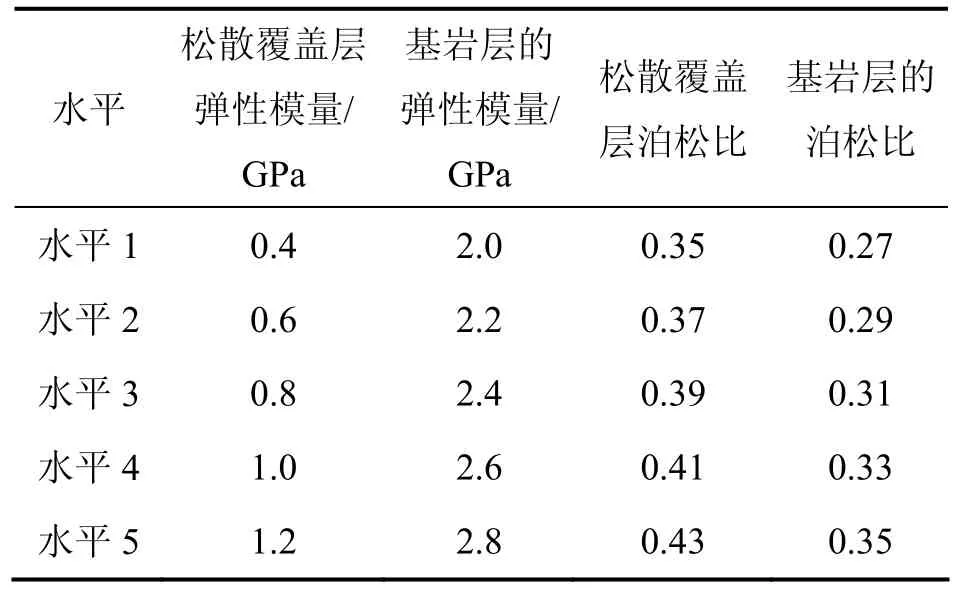
表3 正交设计因素-水平Table 3 Orthogonal design of factor-level

3.5 正交试验优化反演数值计算

按设计好的正交数值试验方案进行计算，最终计算结果如表4所示。根据目标函数值δ越小，解越优的原则，得到试验7为试验的最佳参数组合，即E1=0.6 GPa，µ1=0.37，E2=2.4 GPa，µ2=0.33。

3.6 衬砌工作状态评价

以反演得到的最优岩土参数组合为依据，进行有限元正算分析，得到了隧道左右洞室衬砌的弯矩和轴力，如图5和图6所示。

从图5和图6可以看出：左右洞室所受的轴力和弯矩分布基本相同，在左右洞室的拱脚处负弯矩最大，达-162.049 kN·m；在仰拱靠近拱脚处正弯矩最大，达74.519 kN·m；在左洞室的右拱脚和右洞室的左拱脚部位轴向压力最大，达3 100 kN。由此可以看出：左右洞室的拱脚是最危险部位，应该选取此截面进行安全状态评价。

表4 试验方案参数组合及各测点处计算位移Table 4 Experimentation parameters assembling and computed displacements of keypoints

图5 马鞍山隧道K97+547衬砌弯矩Fig.5 Bending moment diagram of Maanshan lining at K97+547

图6 马鞍山隧道K97+547衬砌轴力Fig.6 Axial forces of Maanshan lining at K97+547

原设计在仰拱部位沿轴向0.5 m长的衬砌内配置环向钢筋为HRB335级，10@22的钢筋，其截面积为3 800 mm2。根据式(4)计算，判断所选断面处于小偏心受压状态。根据式(18)计算得到受压区的计算高度x=301.25 mm；由式(17)得轴心力作用点至受拉钢筋As合力点之间的距离e=238.74 mm；由式(9)～(15)得到衬砌所能承受的最大弯矩值Mmax=182.094 kN·m；然后根据式(19)验算，满足平面外承载力要求。所以，该断面衬砌的安全度为：

可见，马鞍山隧道衬砌处于安全状态，工作状态良好，且具有一定的安全余度。可以适当调整设计方案，使其更为经济、合理。

4 结论

(1) 基于现场监控量测数据，综合运用正交设计理论、有限元理论和钢筋混凝土结构相关理论，提出隧道衬砌工作状态的合理评价思路。

(2) 定义隧道衬砌安全度的概念，并将衬砌的工作状态分为安全、极限和危险3个状态。

(3) 通过正交反演计算和有限元正分析，计算出马鞍山隧道衬砌的安全度为1.124，处于安全状态，具有一定的安全余度。

[1] JTG D70—2004. 公路隧道设计规范[S].JTG D70—2004. Design specification for highway tunnel[S].

[2] 张孟喜, 李钢, 冯建龙, 等. 双连拱隧道围岩变形有限元与BP神经网络耦合分析[J]. 岩土力学, 2008, 29(5): 1243-1248.ZHANG Meng-xi, LI Gang, FENG Jian-long, et al. Coupling analysis of surrounding rocks in double-arch tunnel by FEM and BP neural networks[J]. Rock and Soil Mechanics, 2008, 29(5):1243-1248.

[3] 周建春, 魏琴, 刘光栋. 采用 BP 神经网络反演隧道围岩力学参数[J]. 岩石力学与工程学报, 2004, 23(6): 941-945.ZHOU Jian-chun, WEI Qin, LIU Guang-dong. Back analysis on rock mechanics parameters for highway tunnel by BP neural network method[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(6): 941-945.

[4] 郝哲, 万明富, 刘斌, 等. 韩家岭隧道围岩物理力学参数反分析[J]. 东北大学学报: 自然科学版, 2005, 26(3): 300-303.HAO Zhe, WAN Ming-fu, LIU Bin, et al. Backward analysis of physical and mechanical parameters of surrounding rock of Hanjialing tunnel[J]. Journal of Northeastern University: Natural Science, 2005, 26(3): 300-303.

[5] WANG Zhi-liang, LI Yong-chi, Shen R F. Correction of soil parameters in calculation of embankment settlement using a BP network back-analysis model[J]. Engineering Geology, 2007,91(2/4): 168-177.

[6] 李守巨, 刘迎曦, 王登刚. 基于遗传算法的岩体初始应力场反演[J]. 煤炭学报, 2001, 26(1): 13-17.LI Shou-ju, LIU Ying-xi, WANG Deng-gang. Inversion procedure of initial stress fields in rock masses based on genetic algorithm[J]. Journal of China Coal Society, 2001, 26(1): 13-17.

[7] 李建生, 阳军生, 杨铠, 等. 改进遗传算法在浅埋隧道施工倾斜地表沉降预测中的应用[J]. 公路工程, 2008, 33(6): 46-49.LI Jian-sheng, YANG Jun-sheng, YANG Kai, et al. Application of improved genetic algorithm in prediction of inclined ground surface settlement due to shallow tunnel excavation[J]. Highway Engineering, 2008, 33(6): 46-49.

[8] 蒋树屏, 赵阳. 复杂地质条件下公路隧道围岩监控量测与非确定性反分析研究[J]. 岩石力学与工程学报, 2004, 23(20):3460-3464.JIANG Shu-ping, ZHAO Yang. Study on monitoring and back analysis for road tunnel with complex geology[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(20):3460-3464.

[9] 蒋树屏. 扩张卡尔曼滤波器有限元法耦合算法及其隧道工程应用[J]. 岩土工程学报, 1996, 18(4): 11-19.JIANG Shu-ping. Coupling algorithm of extended kalman filter-FEM and its application in tunnel engineering[J]. Chinese Journal of Geotechnical Engineering, 1996, 18(4): 11-19.

[10] LI Shi-hui, YANG Jie, HAO Wei-dong, et al. Intelligent back-analysis of displacements monitored in tunneling[J]. Rock Mechanics and Mining Sciences, 2006, 43(2): 1118-1127.

[11] TANG Yu-geng, Kung TC. Application of nonlinear optimization technique to back analyses of deep excavation[J].Computers and Geotechnics, 2009, 36(3): 276-290.

[12] 吕庆, 尚岳全, 陈允法, 等. 高填方路堤粘弹性参数反演与工后沉降预测分析[J]. 岩石力学与工程学报, 2005, 24(7):1231-1235.LÜ Qing, SHANG Yue-quan, CHEN Yun-fa, et al. Back-analysis of visco-elastic parameters of filling materials and settlement prediction for high-filled embankment[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(7): 1231-1235.

[13] 许建聪. 降雨作用下浅埋隧道支护参数正交反演分析[J]. 地下空间与工程学报, 2008, 4(5): 897-905.XU Jian-cong. Orthogonal back-analysis of surrounding rock support parameters for shallow buried tunnel under rainfall[J].Chinese Journal of Underground and engineering, 2008, 4(5):897-905.

[14] 李云鹏, 韩常领, 唐明明, 等. 小间距隧道围岩力学参数正交设计反演[J]. 公路交通科技, 2008, 25(9): 107-111.LI Yun-peng, HAN Chang-ling, TANG Ming-ming, et al. Back analysis on mechanical parameters of surrounding rock of tunnel with small spacing using orthogonal design[J]. Journal of Highway and Transportation Research and Development, 2008,25(9): 107-111.

[15] 刘艳青, 卢汝绥. 软岩隧道围岩压力的位移直接反演方法的研究[J]. 土木工程学报, 2001, 34(1): 84-87.LIU Yan-qing, LU Ru-sui. Study on reverse displacement method of ground pressure for tunnels in soft rock[J]. China Civil Engineering Journal, 2001, 34(1): 84-87.

[16] 谢君泰. 乌鞘岭隧道衬砌结构安全性分析[J]. 兰州交通大学学报, 2008, 27(3): 30-32.XIE Jun-tai. Security analysis of Wushaoling tunnel lining structure[J]. Journal of Lanzhou Jiaotong University, 2008, 27(3):30-32.

[17] 周爱红, 张鸿儒, 袁颖. 可考虑任意压力分布形式的隧道衬砌计算分析[J]. 东南大学学报: 自然科学版, 2005, 35(7):95-99.ZHOU Ai-hong, ZHANG Hong-ru, YUAN Ying. Calculation analysis of tunnel lining considering arbitrary surrounding rock pressure distribution[J]. Journal of Southeast University: Natural Science Edition, 2005, 35(7): 95-99.

[18] 侯亚彬. 深埋隧道位移反演及初支可靠性分析[D]. 重庆: 重庆大学资源及环境科学学院, 2008: 51-70.HOU Ya-bin. Displacement back analysis and primary support reliability analysis of deep tunnel[D]. Chongqing: Chongqing University. College of Resources and Environmental Science,2008: 51-70.

[19] 刘福胜, 文竞舟, 王成. 用隧道周边位移反分析围岩压力的解析研究[J]. 地下空间与工程学报, 2007, 7(3): 1203-1207.LIU Fu-sheng, WEN Jing-zhou, WANG Chen. Analytical study on surrounding rock pressure of tunnels by back-analysis on periphery displacements[J]. Chinese Journal of Underground Space and Engineering, 2007, 7(3): 1203-1207.

[20] 赵书学, 李德武. 大跨度黄土隧道钢拱架应力量测与分析[J].公路交通科技: 应用技术版, 2008(1): 159-160, 163.ZHAO Shu-xue, LI De-wu. Stress measurement and analysis of steel arch in loess tunnel with large span[J]. Journal of Highway and Transportation Research and Development: Application Technology Edition, 2008(1): 159-160, 163.

[21] 孙秋红, 胡伟, 李中. 软弱围岩公路隧道初期支护可靠性信息化评价[J]. 采矿技术, 2004, 4(3): 70-72.SUN Qiu-hong, HU Wei, LI Zhong. Information evaluation of reliability of primary support of highway tunnel with weak surrounding rock[J]. Mining Technology, 2004, 4(3): 70-72.

[22] 李德武, 李培天, 高峰, 等. 黄土隧道钢拱架受力量测与有限元分析[J]. 公路, 2005, 8(8): 180-183.LI De-wu, LI Pei-tian, GAO Feng, et al. Stress measurement of steel centering of tunnel in loess and analysis of finite element[J].Highway, 2005, 8(8): 180-183.