测量不确定度评价方法在大型工件现场加工中的应用

赵幸福，田一明，杨 恢，李 伟，梁 爽，李 明

(1.上海大学机电工程与自动化学院CIMS＆机器人中心，上海 200072;2.歌美飒风电(天津)有限公司，天津 300384)

0 引言

随着工业技术的迅速发展，特别是在极端制造方面，对大型工件的加工精度和测量精度要求也越来越高。对于体积庞大、结构比较复杂的物体，传统方法已很难满足现代的测量要，这就需要数字化测量技术。在数字测量过程中，对于大型工件，一次测量很难获取全部信息，这就需要转站测量技术［1］。在测量过程中，由于现场测量环境、转站精度和基准点的设置等诸多因素都会直接影响最终的测量结果，因此评定大型工件现场测量的不确定度是一个急需解决的问题。

1 测量对象分析

1.1 被测工件状况

被测工件是某海上远洋钻井船的船首动力系统，该船排水量为六万吨级。远洋钻井船相当于一个海上移动式的石油钻井平台，在其钻井作业过程中，通过动力系统控制其在海中的位置和方位。为了实现这种要求，钻井船除了具备普通船舶的动力设备外，还在船首设计了三套动力系统。船首动力系统由发动机与动力舱两部分组成。发动机如图1所示，动力舱由图2所示。发动机可以在动力舱内上下移动:发动机移动到动力舱的上部，以便船舶在浅海航行;发动机移动到动力舱的下部，用以实现船舶在海上的定位。

由于发动机有两个工作位置，这就需要在动力舱上下两部分分别安装发动机定位用的锁眼孔和控制发动机移动的导轨。在现场加工过程中，动力舱筒壁需要三等分，每个分度方向上都在上下两部分分别安装锁眼板和导轨，每块锁眼板上加工出两个锁眼孔。由于动力舱筒的直径6m，高度15m。上下锁眼孔的位置度误差不超过0.1mm，显然十二组孔的相互位置关系单靠安装调整，难以达到要求的精度，只能采用安装好锁眼板后，再对锁眼进行现场加工以保证筒中十二个锁眼孔的位置精度。

1.2 测量仪器

传统的测量手段很难满足这种大型工件的测量要求，这就需要数字化测量。激光跟踪仪具有测量精度高、测量距离大、便于携带等优点，在大型工件现场测量中得到了广泛的应用。激光跟踪仪具有测量目标点距离及水平和垂直方向偏转角的功能。距离分量由激光干涉仪测量，角度分量由高精度角度编码器测量。通过每秒几千点的采点速率，跟踪仪通过跟踪内部安装有棱镜反射镜的跟踪球来实现跟踪测量。跟踪球移动时，跟踪仪会自动跟踪反射镜的球心位置。激光跟踪仪通过测量出水平角、垂直角和斜距，然后按球坐标原理得到空间目标点的三维坐标 X，Y，Z［2］。Leica 公司的 LTD840 激光跟踪仪的主要技术参数为:最大测量距离40m，水平跟踪角度360°，垂直跟踪角度 ±45°，最大采样频率3000 Point/S，最大跟踪速度6m/S，测距分辨率1μ，测距重复精度 ±12μ，全量程采样精度25μ，角度分辩率0.14″，全量程角度重复精度 ±7.5μ +3μ/m(2.5*5*10m空间内)，跟踪测量精度(2.5*5*10m空间内)±10μ+5μ/m，全量程测量精度 ±15μ +6μ/m。根据设计，激光跟踪仪满足测量所需的精度要求。

1.3 总体测量思路

大型工件现场加工的测量，工艺是关键。对于圆筒式工件，动力舱又有分度要求，建立柱坐标系比较方便。由于船的发动机安装在船首动力舱，因此，动力舱主轴的精度是影响整个发动机安装精度的关键。考虑到测量基准和装配基准的重合，选取动力舱主轴作为住坐标系的Z轴。但是动力舱是由相关部分焊接而成，所以选取整个动力舱筒轴线为加工和装配体系的基准是不现实的，所以，选取动力舱中有密封要求的上环部分和下环部分。以上环和下环拟合出的轴线为Z轴，船首方向为0度，建立圆柱坐标系。

在实际测量中，如果每次都测量上环和下环建立坐标系，由于被测件是筒壁，难以攀爬，这就增加了测量难度和测量周期。另一方面，对于大型工件，一次测量很难获取全部信息，为了使测量简便易行和缩短辅助测量的时间，采用转站测量的方法。转站测量的原理是，激光跟踪仪在不同的测站进行测量，各测点的坐标就在不同的坐标系内，如果在不同测站上测量一些公共点，就可以将这些点的坐标归算在一个坐标系下。激光跟踪仪利用这些公共的基准点，把在不同测站的测量都归算在同一坐标系下。在首次坐标系建立以后，在下环附上基准点，并测出基准点在这个坐标系下的坐标值。在以后的测量中，只需要测量这些基准点，利用这些基准点就可以建立测量坐标系。测量思路如图3所示。如果假设整个系统是理想状况，那么转站后从不同位置测得的同一基准点的坐标应该完全相同，而实际上各次的测量结果并不相同。跟踪仪用转站原理在不同的测站对这些基准点测量，建立工件坐标系，这种方法显然会产生转站误差。

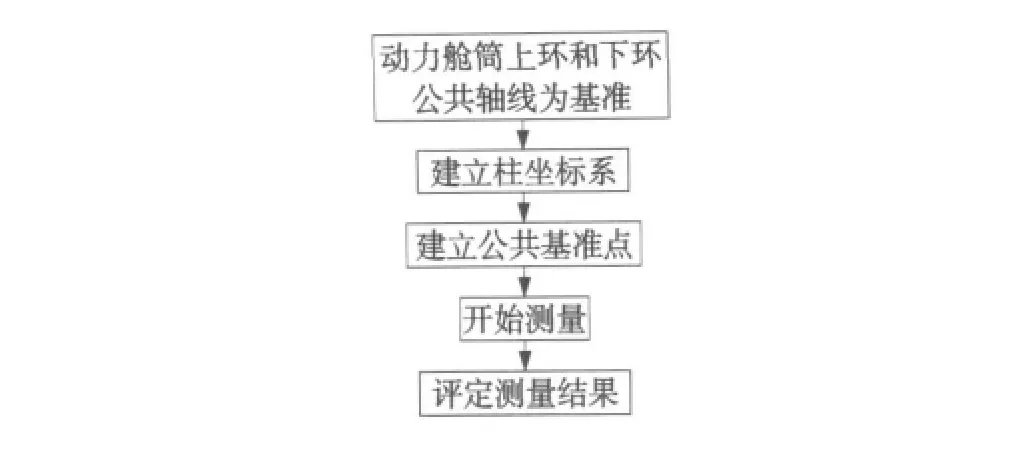
图3 测量思路图

2 测量工艺不确定度分析

大型工件现场测量，需要评定测量结果的准确性以及判定测量工艺是否满足测量要求。按照GB/T18779系列标准，用测量不确定度管理来保障测量精度和测量结果的准确性;用测量不确定度评定规范来评定测量工艺是否满足要求、检验工件的合格或不合格。

2.1 测量不确定度来源［3］

在转站测量中，影响测量不确定度的因素有很多。ISO/TS 14253(GB/T18779系列标准)中描述了数字计量与测量系统中影响被测特性测量不确定度的十大因素，其具体内容如图4所示。这些因素中，测量设备的参考标准器、测量设备、测量设备性能与参数设置都可以按照相应的国家标准进行检定与修正，并在跟踪仪出厂时给出，一般生产厂商会提供相应的补偿方法。能影响测量结果的环境因素有很多，但是激光跟踪仪测量系统的供应商会根据具体情况，对环境条件提出相应的要求，只要能满足这些要求，这些因素就可以被有效地被固定下来，并得到相应的补偿。物理常数和转换因子:激光跟踪仪配有被测工件温度补偿功能。测量评定软件和计算方法:在数字测量中，空间点位信息是通过拟合、计算和评定过程完成的，这其中涉及到大量的计算方法与参数设置问题;算法和参数均由供应商提供，都是成熟产品，而且定期校核。被测量的定义:不完整的或含糊的定义与测量方法，例如不完整的基准定义，过约束的几何要素等，都会影响测量结果的不确定度;但是转站测量过程中很少存在不完整的或含糊的定义的情况，测量人员一般也经过严格的培训。所以以上测量不确定因素本文都不予考虑。由于在测量工艺中引入转站测量，而实际的测量中转站测量又对测量的结果影响比较大，本文主要考虑由于测量工艺引起的测量不确定度。

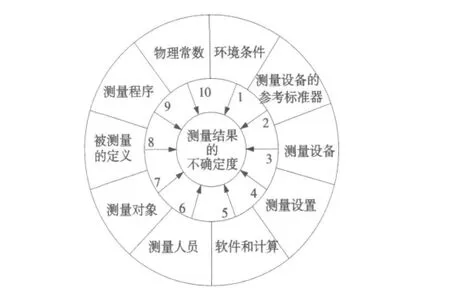
图4 测量不确定度的十大影响因素

2.2 测量不确定度评定流程

在现场测量的情况下，测量任务一般是给定的。在测量工艺确定的情况下，测量方法、测量程序和测量条件都已经是确定的。在给定测量任务的情况下，按照GB/T 18779.2-2004产品几何量技术规范(GPS)工件与测量设备的测量检验的规定，采用简化的逼近法，通过过量估计有影响的不确定度分量，可以得到近似不确定度。给定测量过程的测量不确定度评定流程如图5。给定测量过程的不确定度评定最好采用不确定度黑箱模型进行初次评估，建立初步的不确定度概算，目的是找到占优势的不确定度贡献因素，使其更接近于不确定度分量的实际情况，从而避免过于高估这些不确定度分量。在进行新的评估之前，对全部不确定度贡献因素的相对大小进行分析，改变假设或者改进有关不确定度分量的知识，以得到最大的不确定度分量的更准确的不确定度上界估计值。作第二次逼近评估的不确定概算，再次得到更小和更准确的测量不确定度上界估计值。

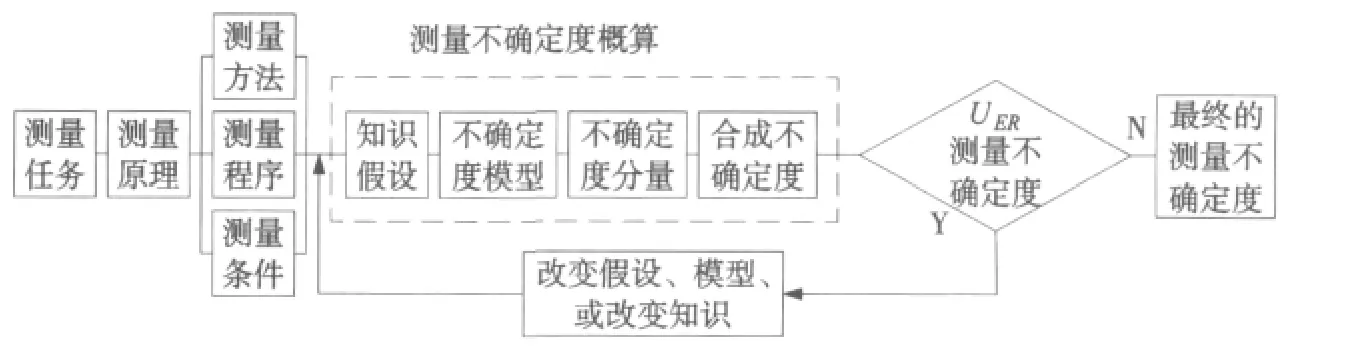
图5 测量不确定度评定流程

采用简化的逼近法，通过过量估计有影响的不确定度分量，为每一个已知的或能预期的不确定度分量提供了在最坏情况下可能出现的上界，从而确保了评估结果的安全可靠，即没有低估的测量不确定度。每一个贡献因素对测量结果不确定度的影响，均以标准不确定度uxx给出，称为不确定度分量。不确定度贡献因素影响的总和称为合成标准不确定度。

2.3 测量工艺引起的不确定度评定方法

根据坐标测量原理，对测量工艺引起的测量不确定度按照单点测量不确定来评定。这一方面是因为在建立测量不确定概算过程中，使用与实际零件尺寸相似的已校准工件替代未知的被测工件的评定方法显然是不合实际的［4］;另一方面，转站测量设置了公共的基准点。这种评定方法综合考虑了测量对象和测量方法与过程规范中的测量不确定度。根据不确定度的性质，评估现场测量单点不确定度的方法是对单点进行多次独立的重复测量，并采用统计方法进行计算。在相同环境下单独采点，跟踪仪给出的测量值围绕一个稳定值上下波动，波动控制在一定范围内［5］。测量工艺引起的测量不确定度评定流程如图6所示。

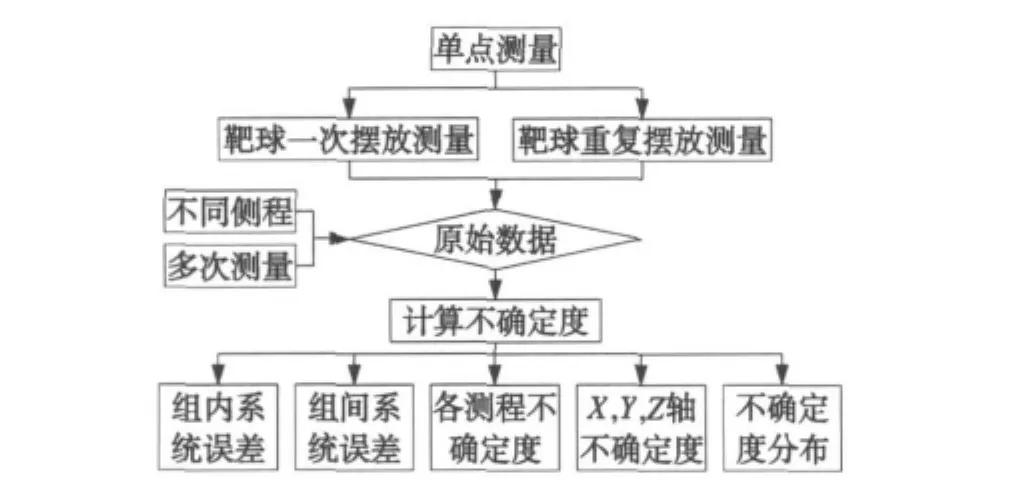
图6 测量工艺引起的测量不确定度评定流程

按两种方案进行单点测量，主要考察各种环境因素对测量结果的影响程度。单点测量不确定度应该按照标准不确定度的A类评定进行评定。对被测量X，在重复性条件下进行n次独立重复观测，观测值为xi(i=1，2，…，n)，算术平均值¯x为:

s(xi)为单次测量的实验标准差，由贝塞尔公式计算得到:

通常以样本的算术平均值作为被测量值的估计(即测量结果)，以平均值的实验标准差s(¯x)作为测量结果的标准不确定度，即A类标准不确定度:

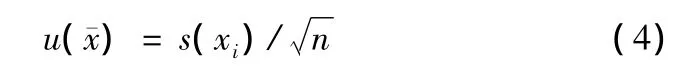
观测次数n充分多，才能使A类不确定度的评定可靠。在处理数据的时候，需要按照莱特准则或格拉布斯准则检查和剔除粗大误差;若有粗大误差，应逐一剔除后，重新计算和s(xi)，再判别直到无粗大误差。莱特准则:若|vi|=3s(xi)，则该误差为粗大误差，所对应的测量值xi为异常数据。使用时要求测量次数充分大。格拉布斯准则:最大残差，若|vmax|=G·s(xi)，则判断对应测量值为粗大误差，其中，G值按重复测量次数n及置信概率pc确定(一般pc=95% 和pc=99%)。判断有无粗大误差后，还需判断有无系统误差。如有系统误差，应查明原因，修正或消除系统误差后重新测量。

3 结束语

由于靶球一次摆放更符合现场的实际测量情况，所以对同一基准点的测量不确定度进行评定过程中，测量数据都由靶球一次摆放获得。对同一基准点按照不同的测程，分别进行多次测量后，用统计的方法计算不确定度。表1为转站后公共基准点在同一坐标系下的坐标值。为了保证评定的准确性，取n=8。

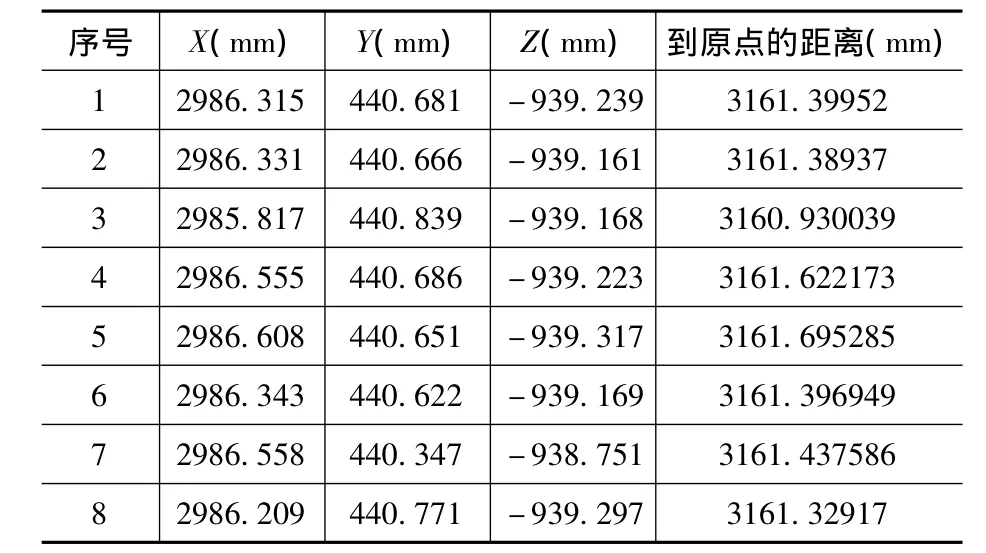
表1 转站后公共基准点在同一坐标系下的坐标值

如果假设整个系统是理想状况，那么转站后从不同位置测得的同一个基准点的坐标应该完全相同，从表中可以看出，各次的测量结果并不相同。基准点的测量不确定度计算如表2。

表2 基准点的测量不确定度计算

由以上数据可以看出，公共基准点引起的测量不确定度为0.0806mm。在本次的测量规划中，引入了转站测量的方法，这使得跟踪仪的测量精度损失很大。但是在大型工件现场加工中，一次测量难以获取全部的被测信息，而且为了缩短辅助测量时间，转站测量是必要的。根据设计要求，本次测量的公差要求都是毫米级，0.08mm左右的转站测量不确定度，显然满足测量的精度要求，本次测量采用的测量工艺也是合理的。

［1］潘国荣，张鹏，孔宁.造船精度控制系统中用移站测量获取点位信息的一种方法［J］.大地测量与测量动力学，2010，5(30):121 －124.

［2］张春富，张军，许文海，等.激光跟踪仪现场测量不确定度的评定［J］.计量学报，2005，26(1):20－22.

［3］中华人民共和国国家标准，18779.2－2004，产品几何量技术规范(GPS)工件与测量设备的测量检验的规定(第二部分).北京:中国标准出版社，2003.

［4］张福民，曲兴华，叶声华.面向对象的大尺寸测量不确定度分析［J］.光学精密工程，2008，16(11):2240－2243.

［5］郁菁菁，李明，张靓，等.激光跟踪仪现场测量的系统不确定度研究［J］.机械设计与研究，2001，23(4):81－83.