反馈控制型PWM DC/DC 变换器的建模分析与混沌控制

杜 杨 韩如成 潘 峰 闻 程

（太原科技大学，太原 030024）

1 引言

混沌控制的概念自1990年提出以来，受到了学者们的广泛重视并进行了大量的研究。时至今日已经取得了一定的成绩，形成了一些较为有效的控制方法。从原理上看主要分为反馈控制方法和无反馈控制方法两大类。其中，反馈控制方法有参数微扰共振法和OGY方法、OPF法、连续变量反馈法、直接反馈法、正比变量脉冲反馈法、变量反馈控制法等。无反馈控制方法有神经网络法、噪声控制法、周期信号法、混沌信号同步法、人工智能法和自适应方法等。但是由于种种原因许多方法并不能应用到电力电子变换器的混沌控制当中。

其一，电力电子变换器是时变性的开关电路，不同的开关状态电路有不同的拓扑结构。根据广大学者的研究经验，构建平均模型并不适合对变换器的研究，而离散迭代模型才是最适合的，这就给我们的建模分析工作带来了很大困难。其二，由于大多数控制方法本身理论的复杂性和局限性使得它不能用于对变换器进行混沌控制。基于以上两种原因本文提出以自适应同步的方法进行混沌控制，并建模分析证明它的有效性。

2 模型的建立与分析

2.1 状态空间平均法

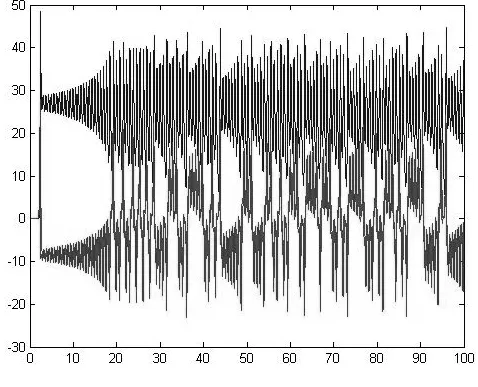
图1 非线性系统中的混沌现象

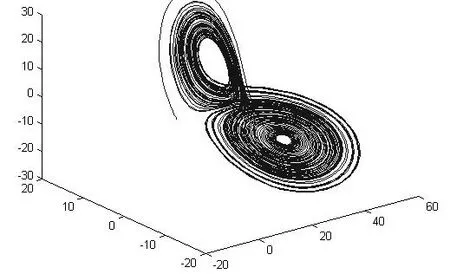
图2 非线性系统中的混沌吸引子

我们先以Buck变换器为例，但是此方法适用所 有的DC/DC变换器。众所周知，Buck变换器是一种开关电路，根据开关频率的和电路元件参数的不同有两种工作状态，分别为电流连续模式和电流断续模式。下面我们以电流连续状态为例来说明。

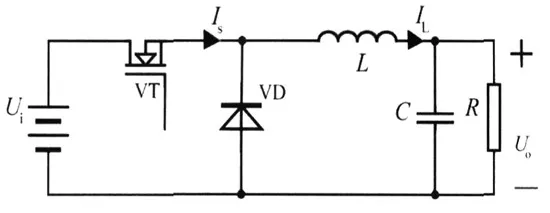
图3 Buck变换器结构图

电流连续模式指的是图1中电感电流Li在整个开关周期中都不为零。在这种工作模式下仍然有两种开关状态，每种开关状态电路的拓扑结构都不一样。状态空间平均法就是根据开关导通时间的不同而对电路进行平均近似建立模型的方法。

设导通和断开时电路的状态方程分别为

其中，1A，1B，2A和2B是方程的系数矩阵，1C和2C为行向量，是系统的状态变量。

把式（1）与式（2）平均化，得到如下的平均方程

向方程中加入扰动量，可把方程转化为

由于上述方程两端的DC项和AC小信号分别相等，所以经过线性化和拉氏变换处理后可以得到系统的传递函数为

将系统的参数带入方程中得

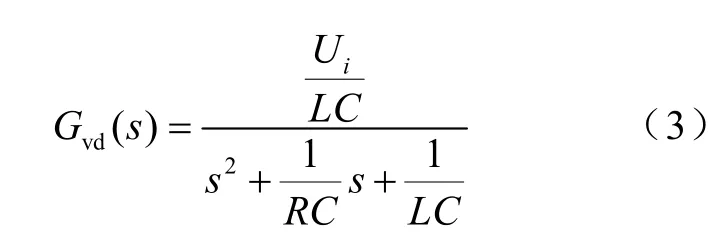
为了验证模型的有效性，选取实验参数值为：

于是可以得到如下的实验结果：

图4 横坐标为Li纵坐标为 Cv

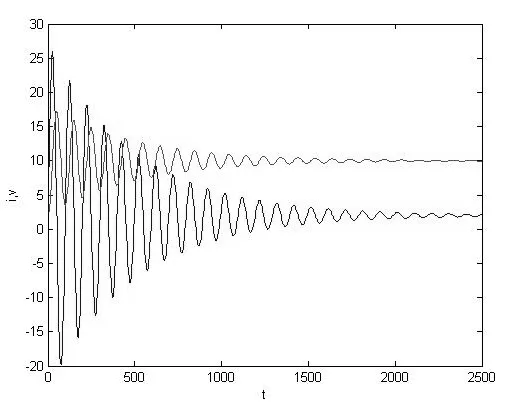
图5 状态变量Li和Cv的变化曲线

图6 实际电路与平均模型的响应曲线

由图3和图4可以看出平均模型可以很好的表示出状态变量的工作曲线。在图5当中1为实际电路的响应曲线，2为平均模型的响应曲线。可以看出平均模型的曲线是平滑过度的，而实际的曲线是有微小的波动，但是平均模型基本可以有效的表示出系统的特性。而通过进一步实验发现，由于线性化的过程使得平均模型很难出现混沌，即它不能表现出原系统丰富的非线性特点，所以平均模型不是我们研究混沌现象的理想模型，实验表明，低阶的离散迭代映射才是我们目前最理想的模型。

2.2 离散迭代映射模型

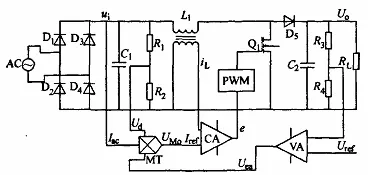
图7 反馈控制型Boost变换器

反馈控制型Boost变换器如图7所示，当开关导通时有状态方程

当开关断开时有状态方程

把时间和能量进行平均化得到如下状态方程

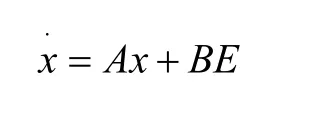
其中，

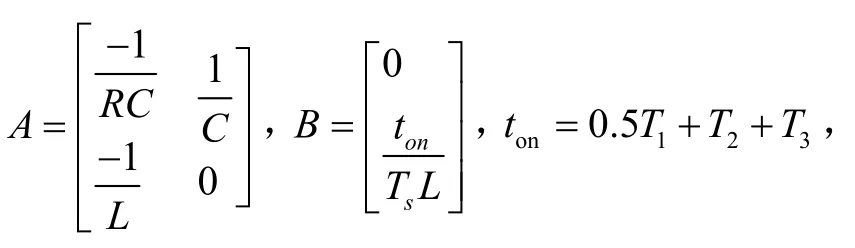
在一个周期内，有上述状态方程可以求得系统的离散迭代模型的标准形式为

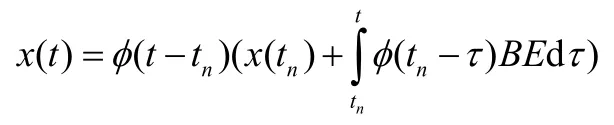
其中

对标准状态方程先进行拉普拉斯变换，然后移项得到如下形式方程

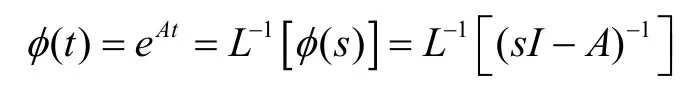
由此导出

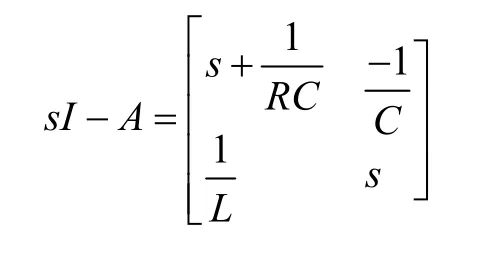
于是带入方程中求拉式反变换，在经过一系列的推导即可得出结果，在此不赘述。

此方法具有一般性，利用它可以得变换器的一阶离散方程或高阶离散方程。比如工作在连续导通模式与不连续导通模式时的一阶离散方程分别为

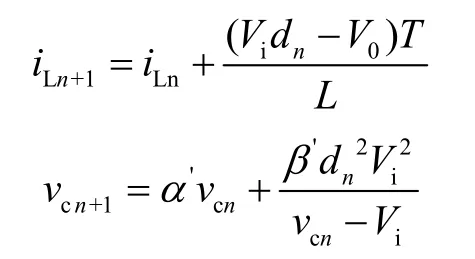
和工作在不连续导通模式下的二阶离散方程

其中工作在不连续导通模式时反馈控制型PWM Boost变换器的一阶离散方程：

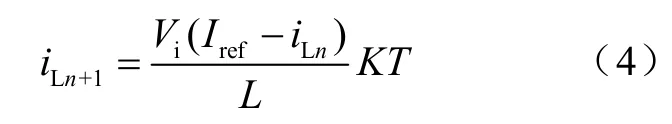
式中，0α，1α，E，M，N， 'α， 'β，K都是和电路元件参数相关的系数矩阵。refI 为基准电流。

3 混沌控制方案

混沌控制的方法有很多，比如参数微扰共振法、反馈控制法、OGY控制法和自适应控制法等等。其中自适应控制方法，灵活多变和简单实用的特点非常适合应用在电力电子变换器复杂的混沌系统控制当中，而且它已经成为这些年混沌控制课题的研究热门。下面介绍一种基于DC/DC变换器的参数自适应同步方法的混沌控制。

由方程式（4）可知，反馈控制型PWM Boost变换器的系统可表示为

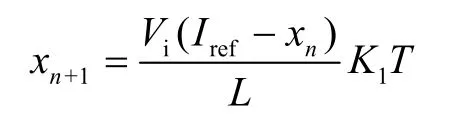
其中我们选择分岔参数为K，目标系统为

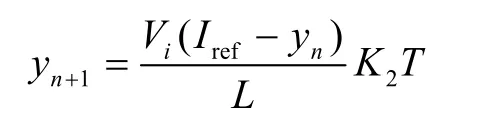
自适应同步控制的目的就是要用参数自适应的方法使两个系统的分岔参数相等，进而使两个系统达到同步状态，即

其中误差系统为

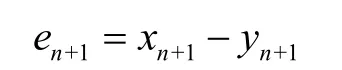
我们知道，混沌系统对初始条件的敏感性是很高的，而且系统对微小扰动也有很高的敏感性。所以试想当同步化误差很小的时候，适当的加入一些反馈，两个系统会很快达到同步。于是我们选取()ut为

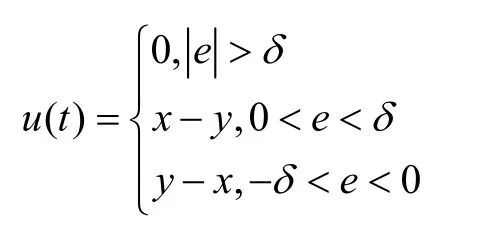
其中e x y= - ，δ代表很小的临域。此种控制方程是用通过正负反馈同时起作用的，减小了同步化误差和最终的误差。经过一定得迭代次数的调节后，响应系统和目标系统将最终实现同步。具体的实验结果如下。

4 验证与仿真实验

下面开始对上文的建模方法和控制方法的有效性进行分析和验证。

根据变换器方程式（4），分岔理论和李雅普诺 夫定理可知，当时，系统是稳定的。也就是说系统在的范围内是稳定工作的。 于是可以选取K作为分岔参数来做实验。于是有

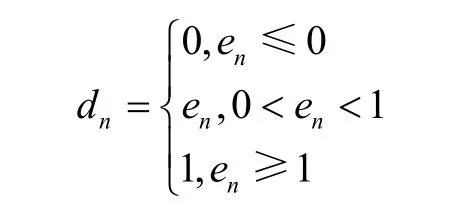
选取系统的参数为i10VV= ，050VV= ，ref12AI= ，

假设两个系统的初始状态不同，根据本系统方程的特点，通过分析添加如下的迭代方程作为控制率。

图8 当K大于1时Ln+1i 的变化曲线

从图中我们可以看出，当K的值超过1时，系统出现不规则的波动。这种波动随着K值的增加变得越来越激烈。系统失去稳定，这就是系统出现混沌的迹象。由稳定性理论可知，当系统出现正的李雅普诺夫指数的时候，系统会出现混沌现象。于是利用Matlab仿真李雅普诺夫指数随K值的变化曲线图如图9。

图9 李雅普诺夫指数随K值变化曲线

由图可知，在李雅普诺夫指数第一次到达0的时候发生分叉，这一点也是系统的失稳点。其实每一次达到0点都是一次分岔，图8就是和系统的倍周期分岔相对应的李雅普诺夫指数的变化曲线。从李雅普诺夫指数的变化可以清楚的看出系统失去稳定走向倍周期分岔的过程。从而验证了上文理论分析的正确性和有效性。

图10 K值逐渐增大时系统的分岔图

从分岔图中可以清楚的看到系统倍周期分岔的产生过程，它的分岔点和李雅普诺夫指数图达到零的点是一一对应的，和我们上文理论分析的结果也吻合的很好。接下来我们采用参数自适应的方法让上述系统与目标系统同步，经过有限次迭代之后可以得到图11、图12所示的结果。

图11 误差系统曲线图

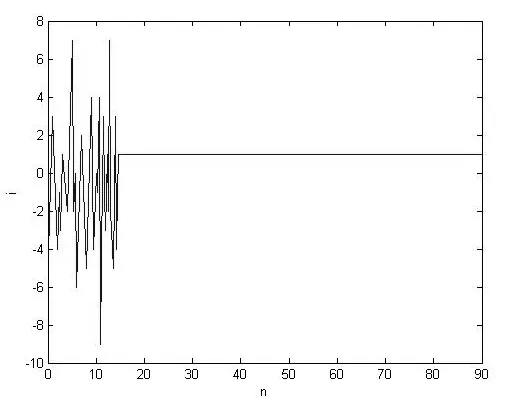
图12 电感电流变换曲线图

由图可见，系统在有限次迭代后很快就与目标系统同步了，误差系统逐渐变为零，电流最终变为恒定。实验结果证明了本文所述的自适应同步的方法能有效的控制DC/DC变换器中的混沌现象。

5 结论

由于电力电子变换器系统的强非线性，使得很多建模方法并不适合用于对变换器的研究，而离散迭代模型才是研究变换器混沌现象行之有效的模型。本文采用有普遍意义的建模方法建立了DC/DC变换器的离散迭代模型。混沌控制的方法有很多种，但是很多控制方法只是消除了混沌但很难让系统回到原来的状态，而混沌同步可以实现。本文采用简洁的参数自适应的方法实现了变换器的混沌自适应同步，在很短的时间内使失稳的系统回到了原先的工作状态，实验结果证明了此方法的可行性与有效性。

[1] 曲颖,张波.电压控制型BUCK变换器DCM的精确离散模型及分岔稳定性分析[J].电子学报,2002,30(8)：1253-1256.

[2] 张波,李萍,齐群.DC-DC变换器分岔和混沌现象的建模和分析方法[J].中国电机工程学报,2002,22(11)：81-86.

[3] 周宇飞,汪莉丽,陈军宁.开关变换器的仿真建模方法及最大Lyapunov指数计算[J].系统仿真学报,2007,19(9)：1925-1928.

[4] 程少庚,崔杜武,等.电网络分析[M].北京：机械工业出版社,1993.

[5] 罗家洪.矩阵分析[M].广州：华南理工大学出版社,1996.

[6] Wood J.R..Chaos：a Real Phenomenon in Power Electronics[J].IEEE Trans.On Circuit and System I,1989(35)：115-124.

[7] Deane J.H.B.,et al.Instability,Subharmonics ,and Chaos in Power Electronic System[J].IEEE Trans.on Power Electronics,1990(5)：260-268.