基于滑模观测器的永磁 同步电动机无传感器控制研究

吴海龙 白连平

（北京信息科技大学自动化学院，北京 100192）

1 引言

永磁同步电动机是一个多输入、多输出的非线性系统，虽然它有比较确定的数学模型，但因其具有非线性及参数时变的特点，应用传统矢量控制技术存在许多缺陷和不足。滑模变结构控制是一种强鲁棒性的控制方法，对系统数学模型精度要求不高，具有快速响应、对参数及外部扰动变化不敏感、无需系统在线辨识，实现简单而且很适合计算机实现等优点。由于滑模变结构控制系统自身的非线性以及高速切换能力，所以特别适用于像交流伺服电机这样的非线性系统的控制[1-2]。

本文采用了一种永磁同步电机无传感器滑模观测法估算转子位置和速度的方法，如图1所示为基于滑模观测器的无传感器PMSM矢量控制系统框图。该方法应用霍尔电流传感器采集相电流和，和经坐标变换得到α-β轴电流和，和经坐标变换得到d-q轴的和，对和进行PI调节得到和，用、及经滑模观测法估算出反电动势和，进而由反电动势得到转子的位置θ∧和速度ω∧信号。系统采用电压空间矢量脉宽调制(SVPWM)策略实现永磁同步电机的无传感器控制。滑模观测器采用饱和函数代替传统的开关函数抑制抖振，滑模估算算法基于数字信号处理器（TMS320LF2407A）实现。系统硬件部分电路以三菱公司的智能功率模块PS21564-N为逆变器，在一台永磁同步电机上进行了实验，实验电机参数如下：额定功率180W，额定电压380V，额定电流0.45A，额定转速1500r/min，极对数2。

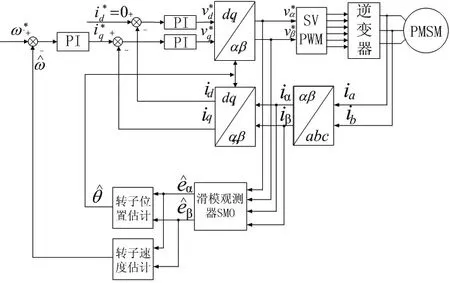
图1 基于滑模观测器的无传感器 PMSM矢量控制系统框图

2 基于滑模观测器的永磁同步电机无传感器控制原理

2.1 定子参考坐标系下的PMSM数学模型

无凸极面装式永磁同步电机在定子坐标参考系下的动态方程可以表示为式（1）

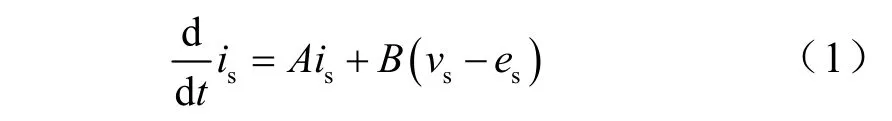
sL、SR和 mψ分别为定子电感、电阻和转子磁链的幅值，ω为转子速度，θ为转子位置角。

2.2 滑模观测器设计

滑模观测器作为一种无传感器控制方法，它以电机的结构为基础，通过分析PMSM数学模型，让获得的电流估计值和实际测量值作偏差，用这个误差不断的修正系统模型，使两者的误差消失，以此来估算转子的转角和转速。

采用滑模观测器估计α-β参考坐标系下的反电势，估算出转子磁通位置和转速。如图2所示，由于只有定子电流可以直接测量得到，滑模面 0sx=（） 选择在定子实际电流上，即，当估计电流到达滑模面时，滑动模态发生，电流估计与实际电流偏差为零。

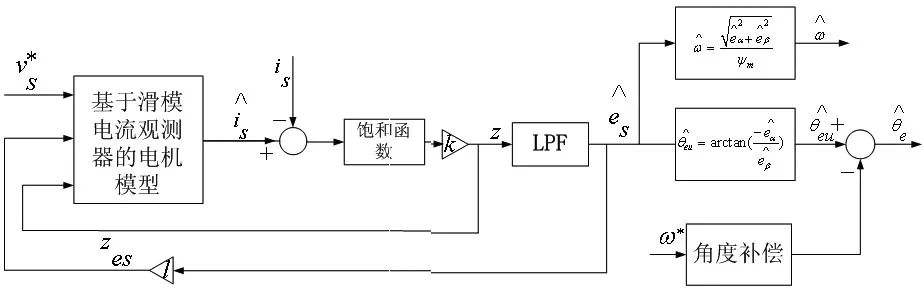
图2 饱和函数抑制抖振的滑模观测器原理框图

滑模观测器设计为表达式（2）、（3）：

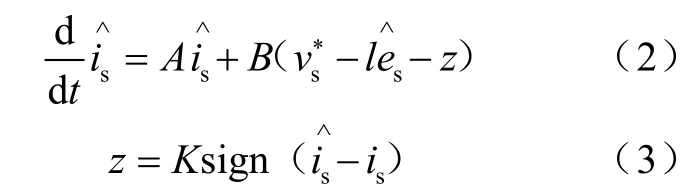
式中，“∧”表示估计值，“∗”表示指令值。

将式（2）和式（3）离散化得到式（4）和式（5）

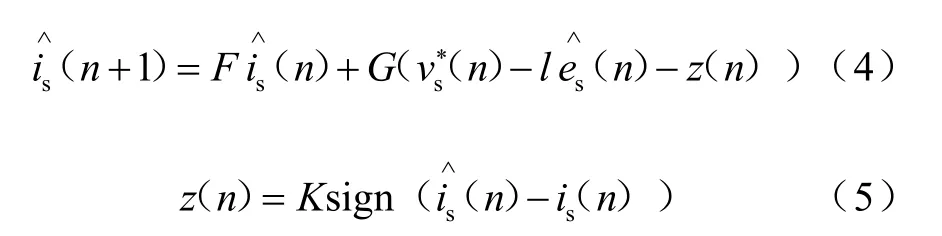
反电势估计值是经过饱和函数输出得到的z，z再经低通滤波器（LPF）得到，如式（6）所示

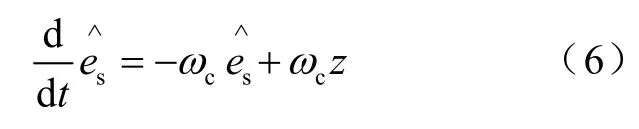
此处，cω为低通滤波器的截止频率。

离散化式（6）得到式（7）

由于

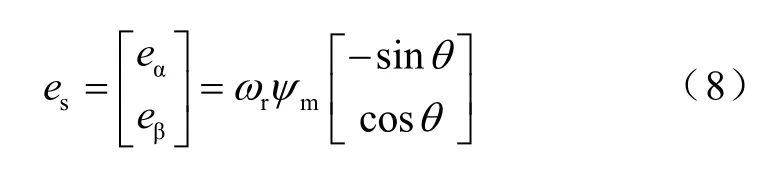
得到转子位置角度为

利用低通滤波器（LPF）获得反电势会带来一定的相位滞后。此相位滞后与低通滤波器的截止频率 cω相关。cω越小，相位滞后越大。基于低通滤波器的相频响应，建立一个相位补偿表，利用给定的速度指令作为相位补偿表的索引得到相位补偿角，与 euθ∧相加，得到转子磁通估计角度 eθ∧。

速度值由反电势幅值计算得到

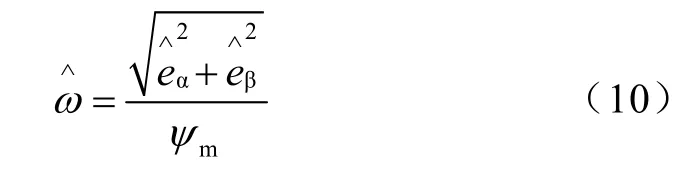
2.3 削弱抖振的方法

滑模控制的执行意味着高频率的切换。滑模变结构控制的激励决定了其输出必然存在抖振，正是这种开关模式实现了系统的鲁棒性。完全消除抖振也就消除了变结构控制的可贵的抗摄动、抗外界扰动的强鲁棒性。因此，对于变结构控制出现的抖振现象，正确的处理方法应该是削弱或抑制[6]。

为了削弱或抑制抖振，采用了替代传统滑模变结构开关函数的饱和函数z，函数曲线如图3所示。

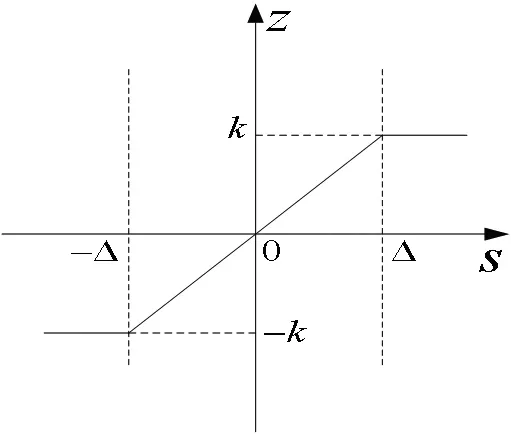
图3 饱和函数曲线

饱和函数z定义如下

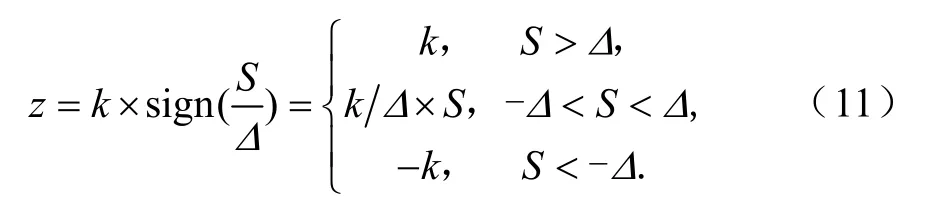
其中，Δ为边界层，k为滑模系数，此系数的选取必须满足可达性和存在性条件，否则滑动模态不能发生。

其中，cω为低通滤波器的截止频率。

此低通滤波器的截止频率 cω可以表示为

转子位置角度补偿角为

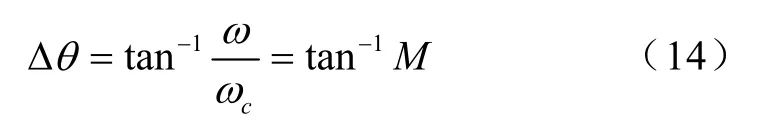
将该补偿角 θΔ 加入到转子位置角度 euθ∧中得到精确的转子位置信号。

2.4 滑模观测器算法的实现

滑模观测估算算法实现是以DSP（TMS320LF2407A）为控制核心，首先由霍尔电流传感器采集a，b相电流，经过A/D转换后得到相电流数字量，经CLARK变换将三相静止坐标系变换为两相静止坐标系，再经两相静止坐标系转换为两相旋转坐标系，转化为直流量，分别与它们的参考输入比较，通过PI调节，得到理想的控制量后再PARK反变换得到输入逆变器的电压空间矢量，计算扇区号及基本矢量作用时间控制逆变器导通和关断。电流环采样频率16kHz。

图4是电流采样及坐标变换算法流程图，图5是滑模观测算法估算转子位置和转速程序流程图，在DSP的开发环境CCS2000中编写程序实现。

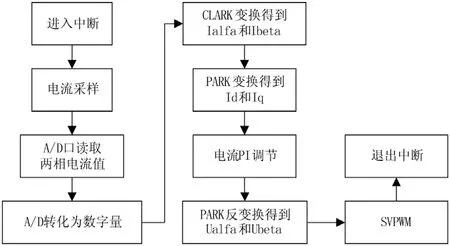
图4 电流采样及坐标变换算法流程图

图5 滑模观测算法估算转子位置和转速程序流程图

3 实验结果与分析

为了验证这种滑模观测法对于电机转子位置估算的准确性，基于上文引言中所述的逆变电路控制方法和实验使用的永磁同步电机，在DSP中编写调试程序，变量通过串行通信总线发送到上位机，通过Matlab绘制图形。图6所示为给定正弦电流与滑模观测法估算实际电流波形的比较。从图中可以看出，估算电流波形有效地跟踪了给定电流波形，且在给定电流形附近有高频率、小幅度的波动，即以给定值与估算值的误差为滑模面产生了滑模运动。

图7所示为给定角度与滑模观测法估算转子角度的比较，由图看出，开始时由于没有到达滑模面，估算角度有一定的偏差，切换到滑模面后，估算角度与给定角度较好吻合，证明了滑模估算转子位置的准确性。通过适当调整参数l、Δ和k可以在一定程度上削弱抖振。

图8所示是电机空载试验转速在900r/min时的U相实际电流波形。图9所示是电机负载转矩0.3N·m转速900r/min时U相实际电流波形。实验表明，此滑模观测估算法能够估算转子位置，电机可以平稳地运行。

图6 电流给定值与滑模观测法估算值

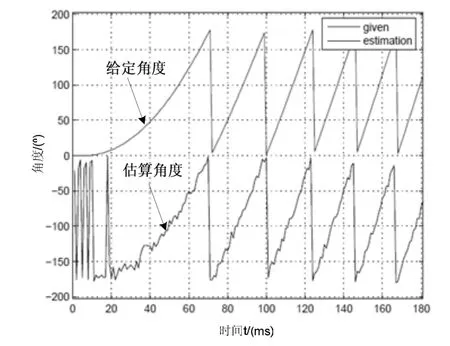
图7 给定角度值与滑模观测法估算值

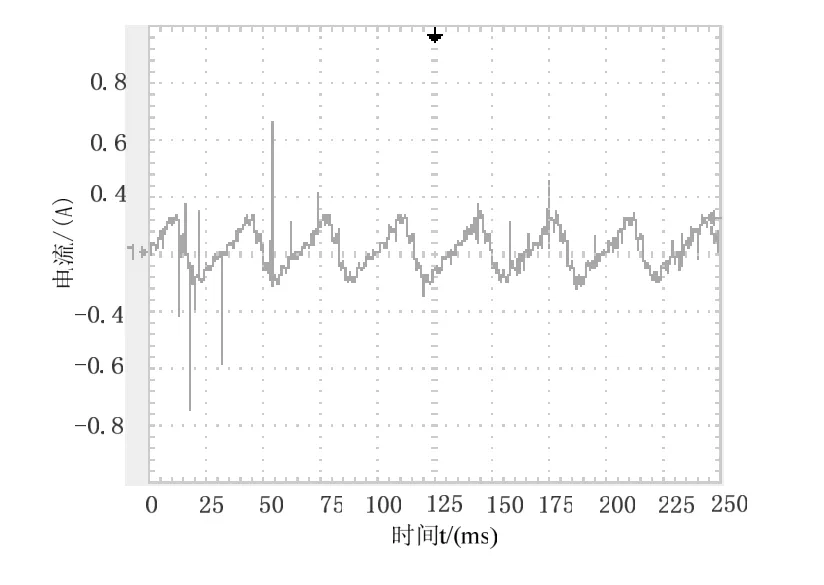
图8 电机空载900r/minU相电流

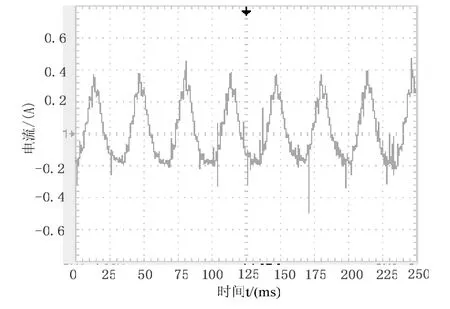
图9 电机负载0.3N·m转速900r/min时U相电流

4 结论

运用于无传感器永磁同步电机转子位置和转速信号估算的滑模观测器方法切实可行，估算转子磁通位置与转子实际位置较好的吻合，应用电机控制专用DSP芯片TMS320LF2407A可以实现滑模观测器估算算法，特别是采用饱和函数能够在一定程度上消除到达滑模面附近时产生的抖振，实验结果表明采用滑模观测法能够实现无传感器永磁同步电机的控制。

[1] Yoon-Seok Han,Young-Seok Kim.The speed and position sensorless control of PMSM using the sliding mode observer with the estimator of stator resistance.TENCON 99.Proceedings of the IEEE Region 10 Conference,vol.2,1999：1479-1482.

[2] 王丰尧.滑模变结构控制[M].北京：机械工业出版社,1995.

[3] 王庆龙.交流电机矢量控制系统滑模变结构控制策略研究[D].合肥工业大学博士学位论文,2007.4

[4] 卞林玉,陈志辉.基于DSP的永磁同步电机无传感器矢量控制系统研究[J].苏州大学学报(工科版),2010,30(1).

[5] 傅涛.基于滑模观测器的永磁同步电机无位置传感器控制[D].天津大学硕士学位论文,2004.12.

[6] 刘金琨,孙富春.滑模变结构控制理论及其算法研究与进展[J].控制理论与应用,2007,24(3)：407-418.

[7] 吴春华,陈国呈,孙承波.基于滑模观测器的无传感器永磁同步电机矢量控制系统[J].电工电能新技术,2006,25(2)：1-3,51.

[8] 吴茂刚.矢量控制永磁同步电动机交流伺服系统的研究[D].浙江大学博士学位论文,2006.6.

[9] 姚琼芸,黄继起,吴汉松.变结构控制系统[M].重庆：重庆大学出版社,1997.

[10] Texas Instruments.Implementation of a speed field oriented control of 3-phase PMSM motor using TMS320F240.Application Report Texas Instruments part SPRA588.1999.

[11] Man Z H,Yu X H.Terminal sliding mode control of MIMO linear systems.Proceedings of the 35th Conference on Decision and Control,1996：4619-4624.