样本量和群内相关系数对整群干预试验中干预效应推断的影响

复旦大学公共卫生学院 公共卫生安全教育部重点实验室(200032) 牟喆 林燧恒

整群干预试验(cluster randomized intervention trial)应用在很多评估干预效果的试验中。它不同于随机干预试验随机分配个体到干预组和对照组，而是随机分配群到干预组和对照组。如:评估青少年中吸烟干预措施、教育领域中新教材的应用、社区健康干预等。但由于群内个体的相关性(intra-class correlation ICC)，分析时需考虑个体的非独立性〔1，2〕。

对整群干预试验效应的估计有很多方法〔3〕，但近年来不少研究都采用混合效应模型(mixed effects model)。一般来说，混合模型中参数的估计以似然估计(ML)或限制似然估计(REML)为主。而对于干预效应的推断，可以用Wald卡方检验，或以此为基础的近似t检验。本文目的在于以Monte Carlo模拟评估样本量和内部相关系数对整群干预试验中干预效应的推断的影响。干预效应的推断通过SAS PROC MIXED的Wald卡方检验和两种不同自由度的t检验。本文对正态结局变量的线性混合效应模型的干预效应进行假设检验和区间估计。

模 型

考虑下面不含协变量的简单的混合效应模型:

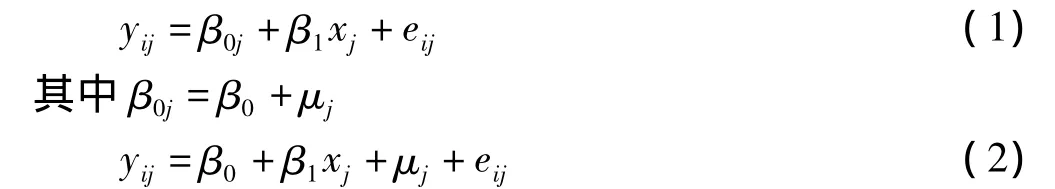
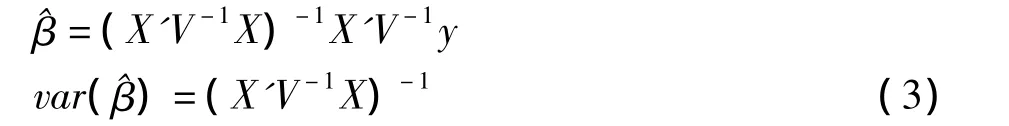
对于干预效应β1的推断，SAS PROC MIXED提供以下统计量〔9〕:

(2)t统计量:在SAS PROC MIXED中的t检验有多种自由度的选择。本文比较containment方法和群方法的 m-2为自由度。Containment是当 PROC MIXED有随机效应时，默认的自由度计算方法;而m-2则是以群为单位的两组t检验的自由度。

模拟试验

模拟一:通过模型(2)利用卡方检验，确定样本量对干预效应检验的影响。设计整群干预试验时，选择适当的群数和群内数，提高检验精度。

模拟二:群数m，群内数n，及内部相关系数ρ对干预效应推断结果的影响。以及卡方检验和两种不同自由度对干预效应推断的比较，为使95%可信区间的覆盖率的精度达到大约0.01，利用SAS 9.1.3对每个参数组合进行独立模拟2000次。

结果解释参数:

第一类错误:在无效假设β1=0时，2000次模拟中P值＜0.05所占的比例。

可信区间覆盖率:β1=1时，2000次模拟中，干预效应估计值的可信区间包含真实值所占的比例。

模拟步骤:

(1)模型(2)中令β1=0，求解第一类错误，在模型(2)中，利用β1=1，求解可信区间覆盖率，并假设1。

(2)产生独立二分类变量Xj(0或1，j=1，2…，m)，0代表对照组，1代表干预组，使得干预组和对照组群数相同(满足均衡设计的试验条件)〔7〕。

(3)产生满足 Xi，m，n 和 N(0)条件下的yij。

(4)模拟结果进行分析，模拟一:利用卡方检验。模拟二:t检验，自由度分别为containment和m-2两种方法。

模拟参数取值:m总群数，n为每群内个体数，ρ为内部相关系数，模拟6×7×6的析因设计。

其中 m(6，10，20，30，50，80)，n(3，10，15，25，50，100，300)，ρ(0.005，0.01，0.02，0.1，0.2，0.5)。

模拟中有些参数的组合如(6，3，0.005)，即总群数m为6(干预组、对照组分别有3个群)，群内个体为3，内部相关系数为0.005，这样的组合可能不现实，但为考虑结果的广义性，都纳入模拟组合中。

结 果

模拟一:根据卡方检验得到的干预效应推断的第一类错误和可信区间覆盖率随参数的变化，得到试验设计时恰当的样本量，从而使干预效应推断更加可靠。分别对每种参数组合做趋势图，由于篇幅有限，选择部分为参考。

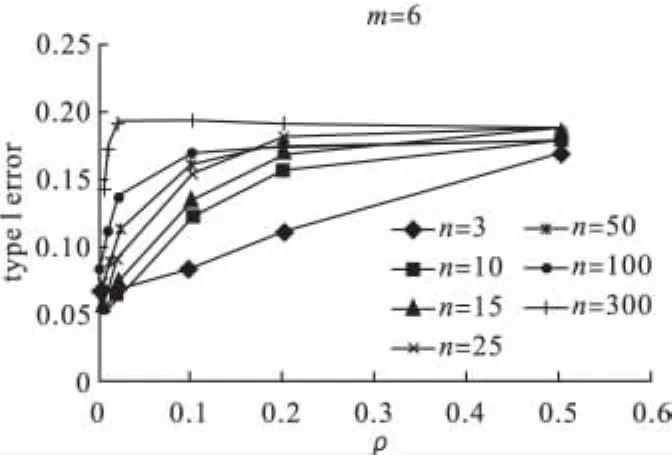
图1 m=6时，对每个固定的群内数n，第一类错误随着ρ的变化图

第一类错误:卡方检验得到的干预效应推断的第一类错误，一般都大于0.05，且会随着内部相关系数ρ的增加而增加。群内数n对第一类错误的影响不大，群数m对结果的影响最大，随着m的增加第一类错误会减小，特别当总群数m＞40后(即干预组和对照组内群数分别大于20)，无论其他两个因素为何值，第一类错误都比较小，从大于0.05的方向接近0.05。因此整群干预试验设计中，为保证干预效应推断的准确性，总群数m应比较大(m＞40)。

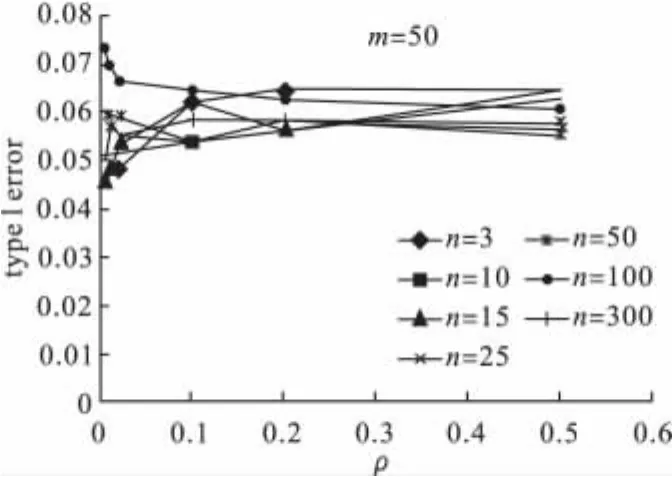
图2 m=50时，对每个固定的群内数n，第一类错误随着ρ的变化图

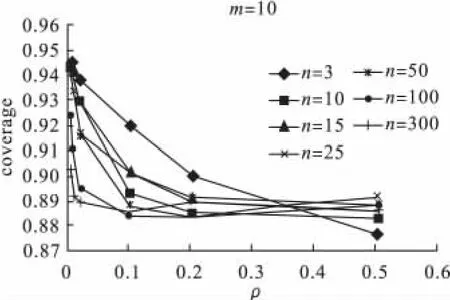
图3 m=10时，对每个固定的群内数n，coverage随着ρ的变化图

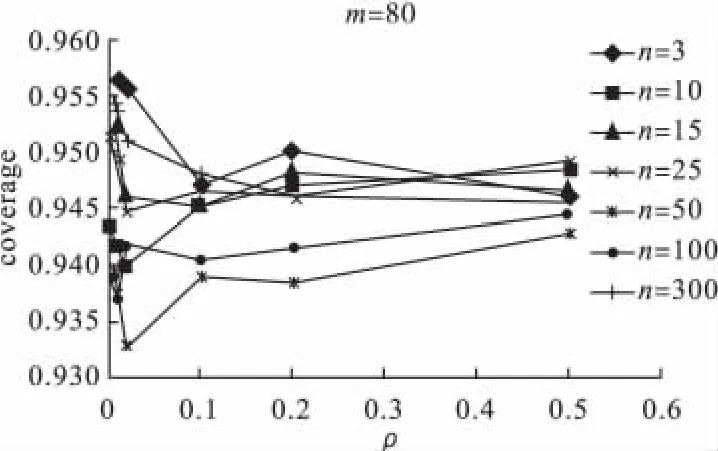
图4 m=80时，对每个固定的群数n，coverage随着ρ的变化图

可信区间覆盖率:卡方检验的干预效应推断的可信区间覆盖率，一般都是小于95%，群数m，群内数n和内部相关系数对覆盖率都有一定的影响，随着内部相关系数ρ的增加，覆盖率逐渐降低，但当群数m增加时(特别当m＞40时)，覆盖率的情况有所改善，如图3的覆盖率最小值在88%左右，图4最小值在93%左右。群内数n对覆盖率影响较小。当内部相关系数小于0.1时，增大群内数n，会使覆盖率降低。但m＞40后，无论n和ρ为何值，覆盖率从小于95%的方向接近95%。

模拟二:卡方检验、t检验中群自由度法和containment自由度法的比较:首先把2000次模拟试验的前1000次和后1000次分别求覆盖率和第一类错误，得到在相同组合下的重复观察值，由glm求得:m，n和ρ的F值较大，交互项中m×ρ的F值较大。t检验的两不同自由度对覆盖率和第一类错误的影响随参数变化趋势同卡方检验相似，但是取值不同，分别看三种方法的变化趋势，和相比较的变化趋势。

第一类错误:卡方检验和containment方法的第一类错误相差不多。当群数小于50时，群自由度法的第一类错误优于卡方检验和containment法，但随着群数的增加，特别当m＞50后，无论内部相关系数为何值，三种推断方法得到的第一类错误差不多。

可信区间覆盖率:卡方检验和containment法的可信区间覆盖率几乎差不多。当群数小于50时，群自由度法的覆盖率高于containment法和卡方检验，但当群数大于50后，三种方法的可信区间覆盖率结果相差不到0.01。

综上所述:为使干预效应推断的精度提高，试验设计时每组群数应大于20。同时，Mixed model中对干预效应推断的三种方法，对可信区间覆盖率和第一类错误受参数的影响趋势大体相同，相比较而言:卡方检验和containment结果相近。群自由度法优于卡方检验和containment自由度法，但当群数大于50后，无论内部相关系数多大，三种方法结果差不多。

讨 论

为提高整群干预试验干预效应推断的精度。本文从设计和分析两方面考虑群数、群内数、内部相关系数对干预效应推断的影响。首先应用自由度为1的Wald卡方检验，得出群数m对覆盖率和第一类错误影响较大，其次为内部相关系数，但随着群数的增加，可以加大覆盖率并减少第一类错误，特别当m＞40，干预效应推断的结果较为可靠。因此，整群干预试验设计时，每组群数最好大于20。其次:分析中由于Wald卡方检验的局限性，提出近似t分布。t分布分母自由度应用SAS MIXED中群自由度法(m-2)，和使用random语句默认的containment方法。文献〔9〕中给出了群方法的第一类错误比较接近0.05，本文通过更广义的选择参数(使结果具有普遍性)，进一步探讨三种方法，当每组群数小于25时，群自由度法优于containment法和卡方检验。但当每组群数大于25后，无论内部相关系数为多大，三方法结果相差不多。SAS PROC MIXED过程中应慎重选择干预效应的推断方法，建议应用群自由度(m-2)的近似t检验法。本研究只考虑均衡的试验设计，不均衡的情况更加贴近实际〔8〕，有待在以后的工作中加以完善。

1.Moerbeek M，Breukelen GJP，Berger MPF.Design issues for experiments in multilevel populations.Journal of Educational and Behavioral Statistics，2000，25:271-284.

2.Donner A.Some aspects of design and analysis of clustered randomized trials.Stat，1998，47:95-113.

3.Moerbeek M，Van Breukelen GJP，Berger MPF.A comparison between traditional methods and multilevel regression for the analysis of multicenter intervention studies.Journal of Clinical Epidemiology，2003，56:341-50.

4.Breukelen GJP，Candel MJJM，Berger MPF.Relative efficiency of unequal versus equal cluster sizes in cluster randomized and multicentre trials.Statistics in Medicine，2007，26:2589-603.

5.Ankenman BE，Aviles AI，Pinheiro JC.Optimal designs for mixed-effects models with two random nested factors.Statistica Sinica，2003，13:385-401.

6.Littel RC，Milliken GA，Stroup WW.SAS for mixed models，Second E-dition.2006，SAS Institute Inc.Cary，NC，USA

7.Heo M，Leon AC.Comparison of statistical methods for analysis of clustered binary observations.Stat Med，2005，24:911-923.

8.Lydia G，Philippe R，et al.Planning a cluster randomized trial with unequal cluster sizes:practical issues involving continuous outcomes.BMC，2006，6:17.

9.Mount J.Small sample inference for the mixed effects in the mixed linear model.Computational Statistics ＆ Data Analysis，2004，46:801-817.