定量测量结果的一致性评价及Bland-Altman法的应用*

山西医科大学卫生统计学教研室(030001) 萨 建 刘桂芬

在临床医学、诊断医学、计量放射学等学科研究中，经常要求对两种或者两种以上诊断方法进行比较或者进行测量结果一致性的评价。有时，其中一种方法是诊断的“金标准”或公认的方法，而另外一种是新的方法或手段，相比较金标准而言可能更加经济或创伤、痛苦更小;而有时并没有金标准，研究者只关注方法之间的互换性如何。通过对诊断或测量结果的一致性评价，可以回答“方法之间能否相互替代”的问题。

当测量结果为定量数据时，涉及到一致性评价的问题，过去临床工作中常用的方法是进行配对t检验、相关分析、回归分析等〔1〕，但是这些方法均不准确，甚至是错误的。例如，配对t检验只是检验两组数据的集中位置是否相同，相关分析只是检验数据同步变化的方向与紧密程度，这些都只是一致性评价的某一个方面。准确的一致性评价，应当同时考虑到数据的集中趋势、离散趋势以及相关性，这三个方面均相同才能认为是“一致”，才能说明方法之间的“可互换性”〔2〕。

通过采用Bland-Altman图来进行定量资料的一致性评价是近年来兴起的新方法，并且针对数据的不同情况，应用方面也有所差别，本文将通过两个实例来介绍该方法的应用，以及需要注意的若干问题。

原理和方法

对定量测量资料进行一致性评价的Bland-Altman方法，最初是由英国学者Bland JM和Altman DG于1983年首先提出的〔3〕，1986年在 Lancet上发表文章详细阐述〔4〕，并于 1999 年〔5〕将该方法进一步扩展。该方法的基本思想是，利用原始数据的均值与差值，分别以均值为横轴，以差值为纵轴做散点图，计算差值的均数以及差值的95%分布范围(即为一致性界限，LoA，¯d±1.96Sd)，认为应该有95%的差值位于该一致性界限以内。分析散点的分布与一致性界限的位置关系，并且与专业上可接受的界限值相比较，如果一致性界限在临床上可以接受，则可以认为两种方法之间一致性较好，可以互换。同时，考虑到抽样误差，除了LoA，还要有LoA的可信区间(LoA CI)。计算LoA CI所对应的标准误一般为 1.71SE(¯d)〔6〕，即可计算出两条一致性界限分别对应的可信区间。

在现有软件中，可以直接绘制Bland-Altman图的只有Medcalc软件，其余的均比较繁琐或者需要编程。通过Medcalc做出的Bland-Altman图一般如图1所示。

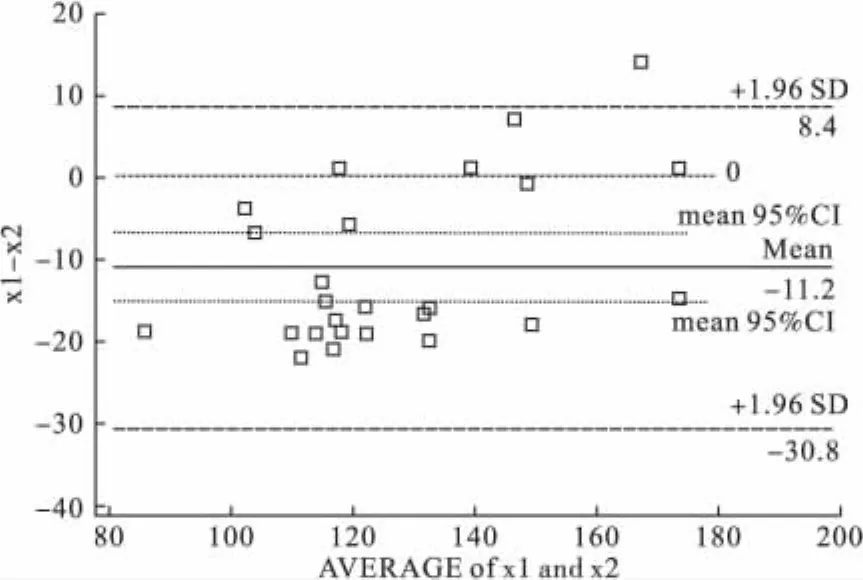
图1 一般的Bland-Altman图(Medcalc软件绘制、有添加)

图1的下方横轴代表两个指标的平均值，左侧纵轴代表两个指标之差。图形区域内共有六条线，三条较长者从上到下依次是:Mean+1.96SD、Mean和Mean-1.96SD，即上述所述差值均数及LoA上限与下限。其余三条较短者(一般无标记，笔者添加)分别为差值为0和差值均数的95%CI。而LoA的95%CI软件不能自动绘出，需要手工计算。一般认为，图形中的点位于LoA范围内的要占到所有点的95%，同时还要考虑该LoA不超出专业上可接受的临界值范围。满足这两点一般即可认为两种方法的一致性较好，可以互换。

实例分析

采用Bland-Altman图进行一致性评价，需要根据数据情形进行判定。如果Difference-Average散点图上差值随均值变化不明显，则可采用原始数据进行作图分析;常见的另外一种情形是差值随着均值的增大而增大，此时需要对原始数据进行对数转换，然后再进行作图分析。具体实例如下:

1.采用原始数据进行分析的实例

(1)原始数据

某实验室采用两个不同公司的试剂盒(W与M)对70份同型半胱氨酸样品进行检测，研究两种试剂盒检测结果是否一致。数据见表1。

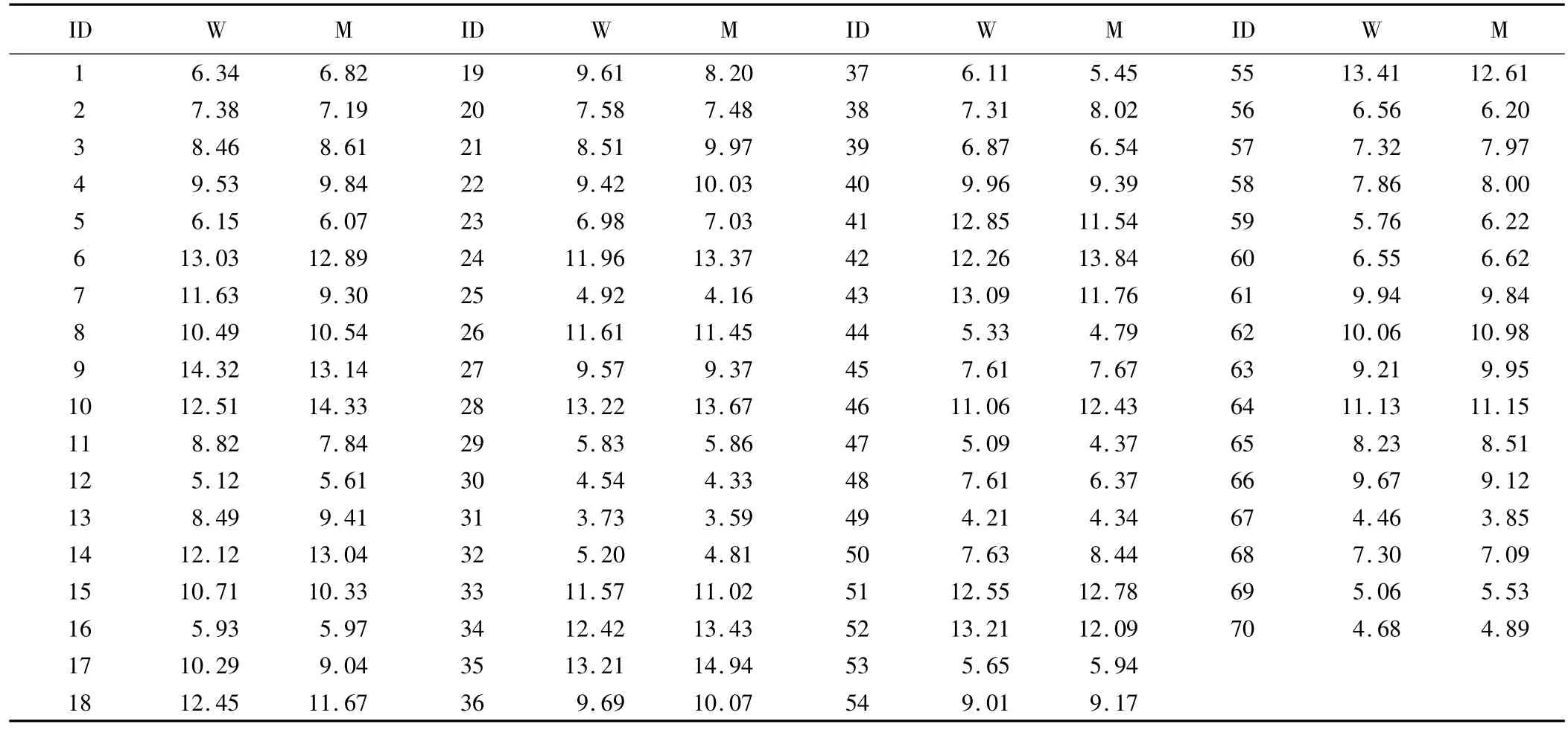
表1 两种试剂盒对同型半胱氨酸检测结果(μmol/L)

(2)Bland-Altman分析

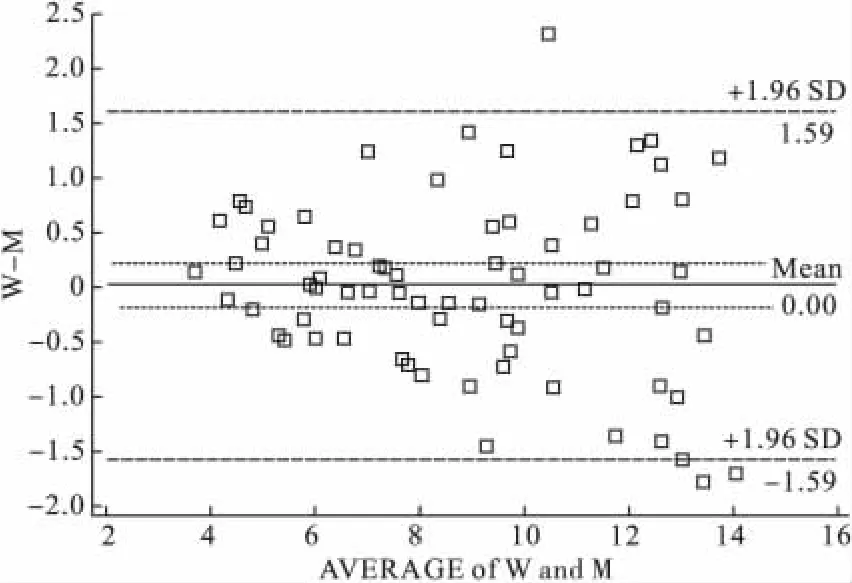
图2 两种试剂盒对同型半胱氨酸检测结果的Bland-Altman图

从图2中可以看出，70个点中有3个位于LoA范围以外，比例为4.29%，小于5%。经过计算，70对数据的相关系数为0.963(P＜0.001)，差值的均数¯d=0.001μmol/L，标准差 SD=0.81μmol/L，标准误 SE=0.10μmol/L，由此计算出的95%LoA为(－1.587，1.589)μmol/L。样本量为 70，对应的 t=1.995，LoA上限1.589的95%CI为(1.589－1.995×1.71×0.1，1.589+1.995×1.71 ×0.1)，即(1.248，2.336)μmol/L，LoA 下限－1.587的95%CI为(－1.928，－1.246)μmol/L。综合起来，LoA的可信区间为(－1.982，2.336)μmol/L。该范围明显大于95%LoA本身，这是考虑到了抽样误差的结果。所以，数据点有95%分布在该范围内即可(比LoA宽泛)，同时也要求LoA的CI不能超出专业意义的临界值(比LoA更严格)，二者其实也是相统一的。假如专业上要求两种检测方法之间的偏差在±2.5μmol/L之间是可以接受的，那么二者的一致性较好。

2.采用经对数转换以后进行分析的实例

(1)原始数据

研究人员采用实时三维半自动边界检测法(A)和实时三维双平面法(B)检测水囊模型的容积，观察两种方法测量结果的一致性，数据见表2。

表2 两种方法对水囊模型容积的检测结果(ml)

(2)Bland-Altman分析

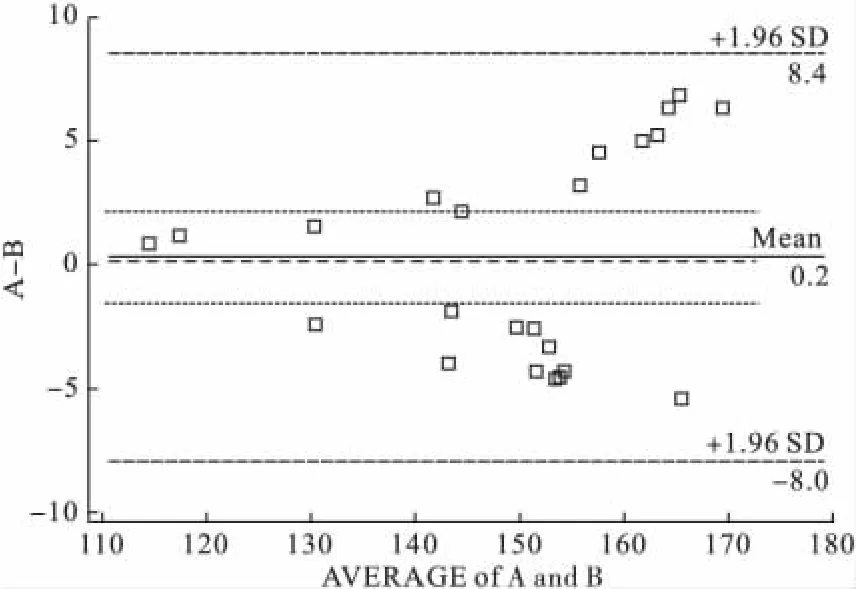
图3 两种方法对水囊模型容积的检测结果的Bland-Altman图

从图3看出，23个点均位于LoA范围内，经过计算，两组数据的相关系数为0.963(P＜0.001)，差值均数 ¯d=0.217ml，标准差 SD=4.17ml，标准误 SE=0.87ml，LoA 范围是(－7.96，8.39)ml，样本量为 23，对应的 t值为2.074，LoA的可信区间为(－11.05，11.48)ml。同时可以发现，A与B的差值随着均值的增加而增大，呈现“喇叭”状分布。可以想到，这样计算出的LoA以及LoA CI一定会由于差值较大的那些点而变宽，要解决这一问题，可以对原始数据进行对数转换，利用转换以后的数据再进行Bland-Altman分析。

从图4看出，经过对数据进行对数转换以后，散点的分布情况有了明显改善。两组对数数据的相关系数为 0.97(P ＜0.001)，对数差值均数 ¯d=0.000419，标准差SD=0.01151，标准误 SE=0.0024，LoA范围是(－0.024，0.024)，经过反对数变换的 LoA为(－1.057，1.057)ml，样本量为 23，对应的 t值为 2.074，LoA的可信区间为(－0.0325，0.0325)，经过反对数变换的 LoA CI为(－1.078，1.078)ml，明显小于原始数据的LoA CI，更容易得到一致性较好的结论。

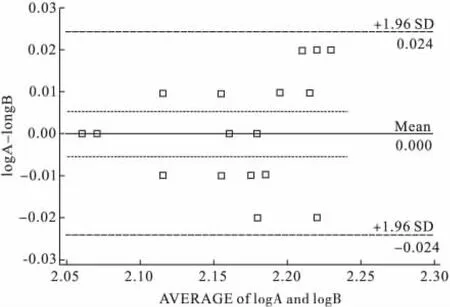
图4 两种方法对水囊模型容积的检测结果对数转换后的Bland-Altman图

讨 论

1.做Bland-Altman图，除了要计算数据的LoA外，还要计算和考虑LoA的可信区间。由于分析的数据大多为抽样得到，所以为了考虑到抽样误差的大小，LoA CI就显得更加重要。LoA CI的范围更大，可以包含更多的散点，但同时也可能超出专业上可接受的临界值。在国外临床文献中，Bland-Altman法应用比较广泛，但是仍然很少有同时考虑LoA CI的，所以该方法的应用不能过于机械化。

2.经过上述两个实例分析比较可以看出，Bland-Altman法的使用一定要根据数据的情况灵活调整，当遇到数据的差值与均值成比例变化时(可能是“喇叭”状的散点，也可能是其他情况)，最好将原始数据取对数以后再绘制该图，然后将得到的LoA与LoA CI进行反对数计算。

3.数据进行对数变化并不能彻底消除差值与均值成比例的问题，但是从上述的图4中也可以看出，这样做可以使得LoA与LoA CI明显变窄，相比较于采用原始数据有更大的优势。

4.采用Bland-Altman图法进行一致性评价实际上也需要有一定的样本量，虽然没有固定的样本含量计算公式，但是样本量越大，LoA CI范围越小，越容易得到一致性较好的结论。同时，除了样本量足够以外，对数据的分布情况也有一些要求，即数据的覆盖范围尽量宽一些，太窄的话容易得到错误的结论，也不容易发现是否存在差值随均值成比例变化的情形。

5.Bland-Altman图法最初主要用于新方法与金标准之间的比较，或者两个观察者间的比较。对于重复测量之间的一致性评价相对比较复杂，还需要进一步深入研究。

1.李镒冲，李晓松.两种测量方法定量测量结果的一致性评价.现代预防医学，2007，34(17):3263-3266.

2.方积乾，陆盈主编.现代医学统计学.北京:人民卫生出版社，2002，81-83.

3.Altman DG，Bland JM.Measurement in medicine:the analysis of methodcomparison studies.The Statistician，1983，32:307-317.

4.Bland JM，Altman DG.Statistical methods for assessing agreement between two methods of clinical measurement.Lancet，1986，i:307-310.

5.Bland JM，Altman DG.Measuring agreement in method comparison studies.StatMethodsMed Res，1999，8:135-160.

6.陈卉.Bland-Altman分析在临床测量方法一致性评价中的应用.中国卫生统计，2007，24(3):308-309.