钻孔法检测残余应力技术中有关参数的数值计算分析

赵冲久，邓雷飞，田双珠

（1.交通运输部天津水运工程科学研究所水工构造物检测、诊断与加固技术交通行业重点实验室，天津 300456；2.长沙理工大学 水利工程学院，长沙 410076）

高桩码头预应力构件的残余预应力检测是人们关注的重点。长期以来国内外学者一直在寻求一种方法能够简单、快捷、准确地测出在役构件的残余预应力。德国学者J．Mathar在1934年提出了使用钻孔法测量构件残余预应力，由于其具有操作简单、对构件损伤小的特点，目前已得到广泛应用［1］。该方法采用机械切割，在具有残余应力的构件上钻一个小孔，使其邻域内的应力得到释放而产生相应的应变，通过测量应变换算出构件原有的应力。根据钻孔的深度可分为通孔法和盲孔法［2-3］。由于码头的预应力构件通常较大，采用通孔法施工难度大、对构件的损伤大，而盲孔法只在构件表面钻到一定深度，不穿透构件，大大降低了对构件的损伤程度。本文以天津港某码头在役预应力轨道梁的残余预应力检测为例，描述了有关参数的计算方法。为减少现场工作量和施工的盲目性，提高检测工作的安全性和可靠性，检测前需要通过有限元法，确定检测工作中的最佳孔径、孔深和粘贴应变片的位置等重要参数。

1 理论依据

钻孔法的基本理论来源于弹性力学，假设一个承受双向均布拉力σ1、σ2（σ1>σ2）的矩形薄板或长柱（图1），在平板（或长柱）任意点处，采用机械切割的方式开挖一个半径为r的小孔后，板内应力就会发生扰动。根据圣维南原理，孔口邻域内（一般为距孔边1.5倍孔口尺寸）的应力分布将会有显著改变，而距孔口较远处的应力分布则基本不受影响。根据钻孔前后应力的分布状况不同，得出孔口附近由于钻孔引起的应力改变量为

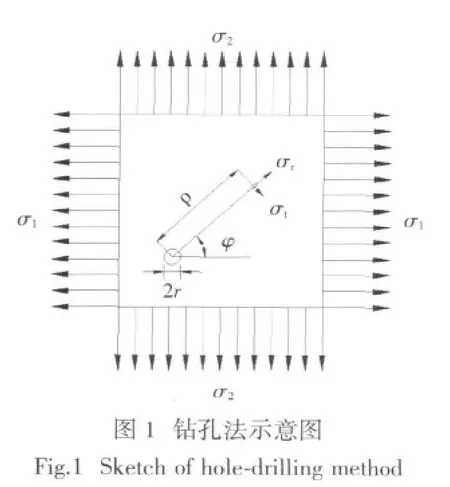
Δσr，Δσt为点A因钻孔而产生的应力差，那么在点A处将相应地产生应变，并且有

将式（1）代入式（2），即可以建立点A的径向应变Δεr与主应力σ1，σ2与主方向φ之间的关系式

根据式（3），只需要在薄板上测量出与钻孔中心夹角相同的 3 点 a，b，c的径向应变 Δεra，Δεrb，Δεrc，列出3个方程，即可以求得主应力σ1，σ2与主方向φ。于是问题就归结为径向应变的测量。通常预应力钢筋混凝土梁的上下表面处于单向应力状态［4］（即只有压应力或拉应力，假设梁的轴线方向为x轴），则σ1=σx，σ2=σy，φ=0。测试时可在梁的测点沿着工作应力的方向粘贴电阻应变片，通过钻孔释放应力，从而产生应变，用电阻应变仪来测定应变Δεx，则式（3）可改写为

将式（4）代入式（2）求得轴向应变为

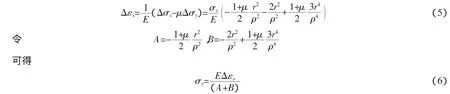
式中：λ=2r/h。式（7）适用于 1＞λ≥0.4，而 λ＜0.4 时则偏差较大，将，代入式（6）可得

2 工程概况

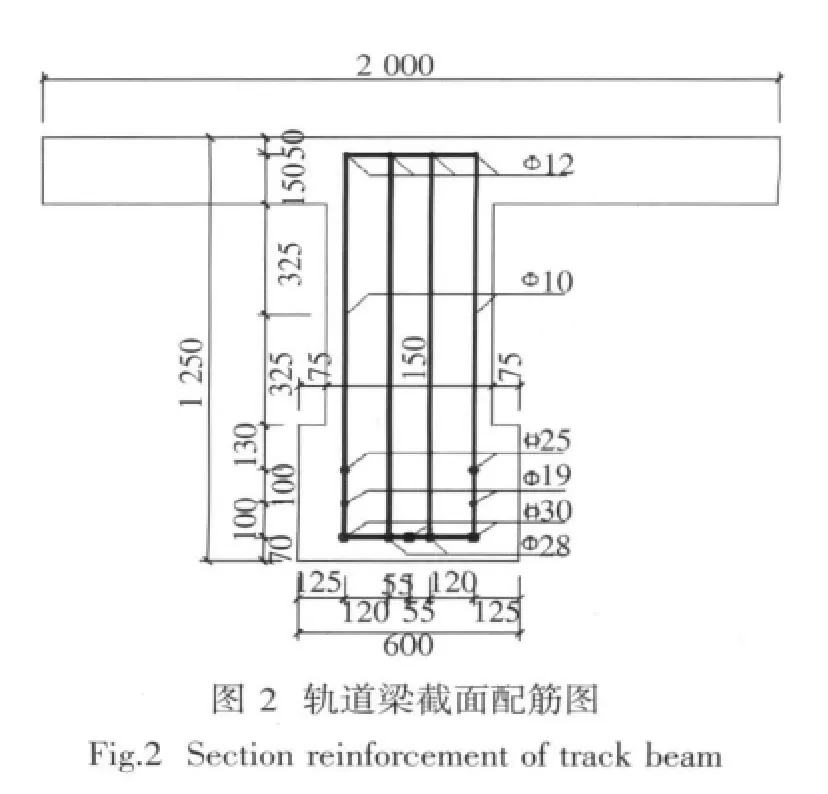
天津港某码头混凝土预应力门机轨道梁建造年代较新，且近几年工作性能良好。在提高门机型号前要对其安全性进行评估，需检测其残余预应力。该梁为配有预应力和非预应力筋的非对称I形截面梁，采用分段预制，吊装完成后现浇固结成一个整体。每7跨为一个结构段，每跨梁全长7 000 mm，梁高1 250 mm，梁宽450 mm，下翼宽600 mm，上翼宽2 000 mm，下翼厚400 mm，上翼厚200 mm，混凝土等级为C35，保护层厚度70 mm。箍筋为I级10号钢筋，梁的基本尺寸和配筋情况如图2所示。

3 有限元计算模型

3.1 模型设计

由于检测对象为在役结构，钻孔选择在应力水平较高、较易测量的梁腹底板。由于边界条件的约束将会在梁底两端形成应力集中的现象，为尽量减少这种现象对孔口应力测量造成的影响，钻孔应距两端一定距离。为减少计算量，钻孔位置选择在梁底对称中心。面层和轨道等其他附属设施因对梁的作用较小，建模时作简化处理忽略其对结构的作用，假定梁只受自身预应力和重力的作用，不受任何其他外力［5］。考虑到钻孔深度受到钢筋布置的限制，孔的深度不能大于梁底部的保护层厚度αs=70 mm，为寻找参数变化时应力变化规律，设置了2组模型，第一组模型为同一深度（50 mm）不同孔径（30 mm、40 mm、50 mm、60 mm、70 mm 5项参数）时的对比组；第二组模型为同一孔径（50 mm）不同孔深（30 mm、40 mm、50 mm、60 mm、70 mm 5项参数）时的对比组，总结参数改变时应力应变的变化规律。

3.2 建模

采用分离式模型分别考虑混凝土和钢筋的作用。混凝土是抗压能力远大于抗拉能力的非匀质材料，采用solid65三维实体单元，该单元可模拟混凝土的开裂（3个正交方向）、压碎、塑性变形及徐变。预应力钢筋采用每个节点具有6个自由度，支持弹性、蠕变和塑性的beam188三维梁单元模拟。使用降温法模拟预应力施加过程［6］。模拟在役混凝土预应力梁不加荷载工况下，钻孔混凝土表面受拉区压应力的应力释放。首先为预应力钢筋单元设定一个初始温度，并且给定一个降温值，使预应力钢筋单元产生收缩变形，钢筋收缩将使钢筋产生预拉的作用。此时钢筋对应的应力就是预应力。钢筋的热膨胀计算公式如下

式中：ΔT为预应力钢筋降温值；Ep为预应力钢筋弹性模量；α为预应力钢筋线膨胀系数，通常取α=1.2×10-5/℃。

有限元计算中用到的主要参数包括预应力钢筋弹性模量Ep=1.8×105MPa，泊松比μp=0.3；非预应力钢筋弹性模量=2.1×105MPa，泊松比=0.3；混凝土弹性模量 Ec=3.15×104N/mm2；混凝土密度 ρ=2 480 kg/m3；泊松比μc=0.2；拉伸成体单元采用mesh200单元。混凝土本构关系按照新修订的《混凝土结构设计规范》（GBJ50010-2002）计算得出。I级钢筋的抗拉强度设计值fy=210 N/mm2；II级钢筋的抗拉强度设计值fy=360 N/mm2。网格划分采用扫略的方式生成，网格密度为50 mm，在钻孔附近加密网格［7］。重力加速度取g=9.8 m/s2。因预应力梁不受外力为自由状态，钻孔位置在腹底板正中心且钻孔后对远处的影响小，故将其作为简支梁处理，加约束时一端梁底施加竖直和水平方向的约束，另一端只施加竖直方向的约束［8-10］。模型可以分为2种不同状态，第1种状态为不钻孔条件下，其计算结果作为工况1，第2种状态在第1种的基础上进行钻孔，将计算结果作为工况2。然后将2次计算的工况结果相比较，得出钻孔前后应变的差值，此差值即为钻孔后测点处的应变。

4 有限元结果分析

模型计算结果如图6所示，钻孔后孔轴向应变释放量和影响范围都比横截面方向大，这与实际情况相符合。提取第1组计算结果进行轴向应变分析，预应力梁底中心轴向的部分节点应变值见表1。由表1可知，同一孔深（50 mm）时，钻孔孔径越大，孔口邻域内的应变释放量也越大，孔径70 mm时最大释放应变量达到97.7×10-6ε，影响的范围也是最大的，这与实际情况相吻合。应变从孔口开始由近及远迅速降低，当距离达到150 mm后，所有的应变值都下降至10-6ε以下，之后下降的速度开始减缓。考虑到电阻应变片最小读数为10-6ε，低于此应变值时可忽略不计。因此测试点布置时不宜超过距钻孔中心150 mm。在提取横向应变分析时发现，钻孔处产生的集中应变量相对较小，且影响范围也相对较短，可测范围在50 mm以内，应变不易测量，因此测点不宜布置在横向，且应变片也不宜横向粘贴。

提取第2组结果中的梁底中心轴向应变值（表2），数据分析可以发现，相同孔径（50 mm）的情况下，随着孔深的增大，应变的释放量也相应增大，钻孔深度达到70 mm时为最大应变量71.2×10-6ε，且最大应变产生的位置都为距孔中心点约33.3 mm处，达到150 mm时应变都下降到10-6ε以下，该值不在应变片的分辨范围之内，可忽略不计；比较2组结果，还可以发现孔径尺寸对应变的影响比孔深大，孔径每增加10 mm，最大应变平均增大15%，而孔径不变、孔深增加时，最大应变基本不变。因此在条件允许的情况下，可适当加大孔径。

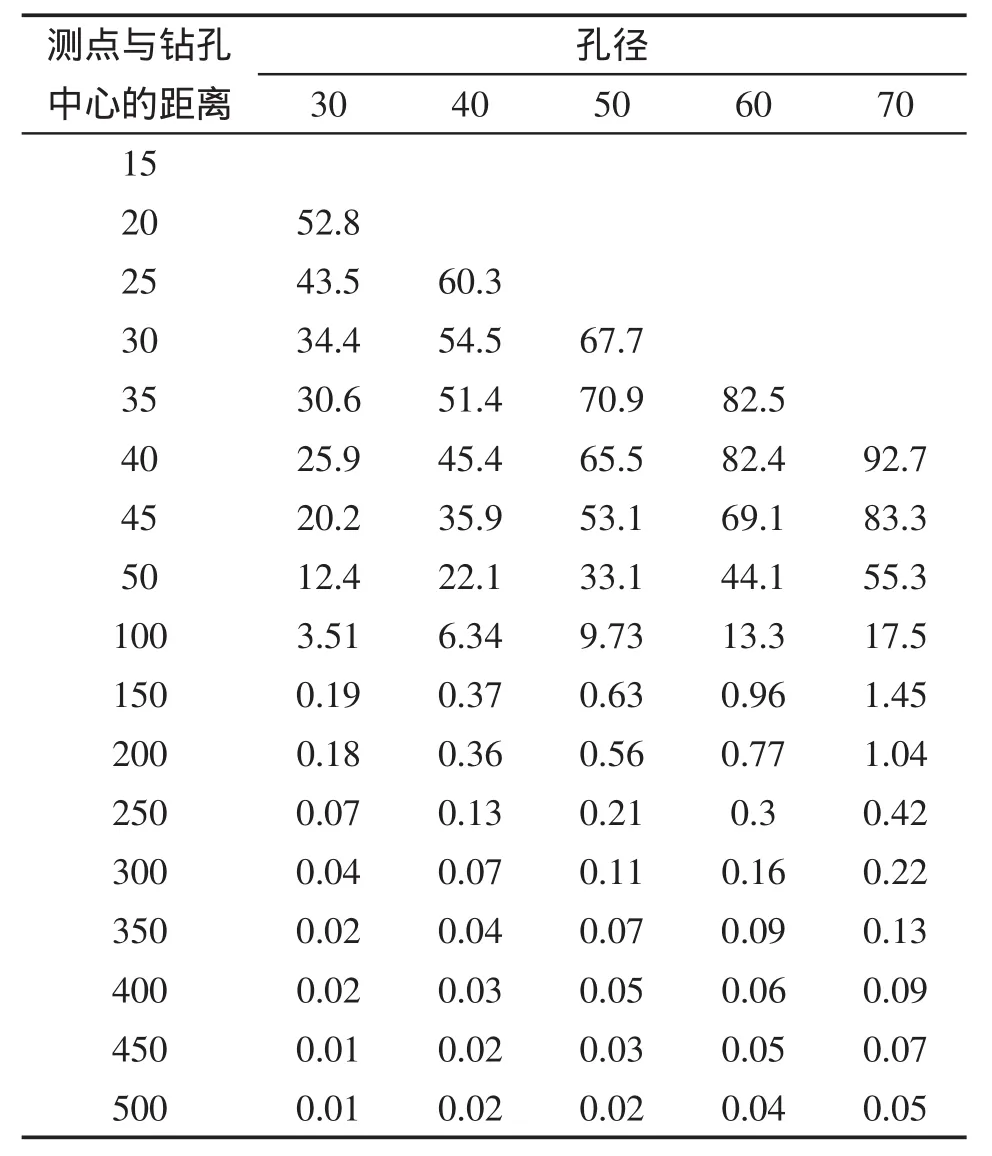
表1 第1组提取节点轴向应变值ε（10-6）Tab.1 Extracted axial strain of nodes of the first group mm

表2 第2组提取节点轴向应变值ε（10-6）Tab.2 Extracted axial strain of nodes of the second groupmm

由有限元计算的结果可知，未钻孔时梁在预应力的作用下出现反拱现象，受拉区混凝土受压，梁底中心轴向实际应力为-1.94×106Pa。钻孔后，孔口附近的应力释放，根据钻孔前后的应变差，按式（9）计算出梁底中心轴向应力的计算值，分别分析在相同深度、不同孔径和相同孔径、不同孔深时计算应力的变化趋势，然后将2种情况与梁底实际应力相比较（图7～图8）。由图7～图8可见，当孔径孔深2个参数变化时，计算应力总在50 mm和100 mm两点处较接近梁底应力的真实值。50 mm处离钻孔位置太近，不易测量应变，因此测点宜布置在100 mm处。固定其中一个参数，当孔深不变时，孔径越大该测点的计算值越接近实际施加应力值；而孔径不变时，孔深越浅，计算值越接近实际施加应力值。当2r/h=1，即孔径孔深都为50 mm时，钻孔法计算的结果为-1.94×106Pa，与梁底实际应力相吻合，此时的应变在可测范围之内，故钻孔孔深和孔径都为50 mm时为最佳。

5 结论

通过改变孔径孔深2项可变参数，分别计算出钻孔前后的应变差，进一步得到计算应力的变化规律。提取钻孔前梁底中心处的轴向实际应力与计算值相比较，结果表明孔径和孔深都为50 mm，在梁底中心轴向距钻孔中心100 mm处的计算应力与实际施加应力吻合。即为所求的最佳孔径、孔深和粘贴应变片位置。钻孔法检测残余预应力中参数的确定非常复杂，涉及的因素众多，例如预应力梁的断面形式、配筋条件等。在确定类似构件参数时，还应根据实际情况进行分析，以便得到更合理的参数。

［1］刘丹娜.利用钻孔法对在役桥梁进行有效预应力的估计［D］.武汉：武汉理工大学，2008.

［2］黄福伟.无粘结预应力空心板桥混凝土现存预应力检测的计算分析［J］.公路交通技术，2008（6）：81-83.

HUANG F W.Calculation and Analysis of Existing Prestress Detection of Concrete in Nobonding Prestressed Cored Slab Bridge［J］.Technology of Highway and Transport，2008（6）：81-83.

［3］刘忠亚.利用钻孔法估算在役混凝土结构现存预应力［J］.武汉工程大学学报，2008，30（4）：62-64.

LIU Z Y.Permanent prestress evaluation of prestressed concrete bridges in-service by hole-drilling method［J］.J.Wuhan Inst.Tech.，2008，30（4）：62-64.

［4］王小明.预应力混凝土梁钢筋残余预应力检测研究［D］.哈尔滨：哈尔滨工程大学，2008.

［5］刘龄嘉.在役混凝土简支梁有效预应力计算［J］.交通运输工程学报，2005，5（3）：47-51.

LIU L J.Effective prestress computation of existing PC simply-supported beam［J］.Journal of Traffic and Transportation Engineering，2005，5（3）：47-51.

［6］谢功元.在役混凝土梁永存预应力试验研究［D］.西安:长安大学，2004.

［7］Sasaki K.The Accuracy of Residual Stress Measurement by the Hole-drilling Method［J］.Experimental Mechanics，1997，37（3）：250-257.

［8］张耀庭.有粘结预应力混凝土简支梁的非线性有限元分析［J］.华中科技大学学报，2007，24（1）：13-16.

ZHANG Y T.Nonlinear Finite Element Modeling of Simply Supported Bonded Prestressed Concrete Beams［J］.J.of HUST.，2007，24（1）：13-16.

［9］金国芳.梁腹开洞后受力分析的荷载试验及有限元计算分析［J］.四川建筑科学研究，2001，27（2）：1-3.

JIN G F.Study on the loading test and finite element analysis of a holing beam［J］.Building Science Research of Sichuan，2001，27（2）：1-3.

［10］梁文彦.无粘结预应力混凝土梁非线性有限元分析方法研究［J］.哈尔滨工程大学学报，2004，25（4）：461-463.

LIANG W Y.Nonlinear finite element analysis of unbonded prestressed concrete beams［J］.Journal of Harbin Engineering University，2004，25（4）：461-463.