透空式梳式防波堤的数值模拟和波浪透射系数的研究

房 卓，张宁川，臧志鹏

（1.大连理工大学海岸和近海工程国家重点实验室，大连 116023；

2.中国科学院力学研究所水动力学与海洋工程重点实验室，北京 100190）

近几十年来，数值波浪水槽的发展及应用取得了巨大进步。王永学采用线性造波机理论，应用VOF方法给出了可吸收数值造波边界条件，即造波板的运动除产生行进波外，同时产生一个抵消反射波的局部振荡［1］。李凌等通过在动量方程中添加附加源项，发展了黏性流数值造波和消波的方法，并模拟了波浪与2个垂直刚性薄板的相互作用［2］。高学平等利用源造波法模拟不规则波浪，并结合阻尼层消波技术模拟消除波浪遇结构物后形成的二次反射，研究了半圆形和台阶形防波堤的堤前波浪力的分布规律和消波效果［3］。周勤俊等利用动量源方法造波，对海堤上的越浪进行了数值模拟［4］。数值方法已经成为研究波浪与防波堤的相互作用的一种重要手段［5-6］。

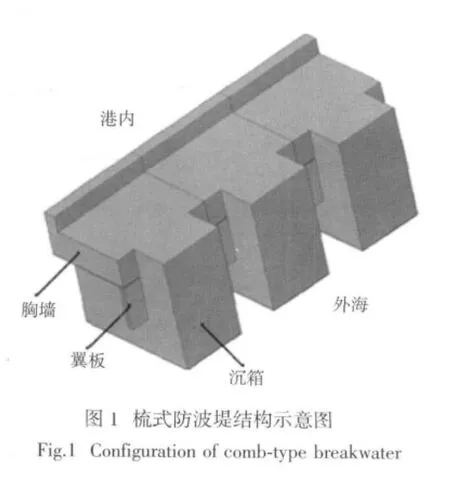
梳式防波堤是近年来出现的新型防波堤，在传统直立防波堤基础上，用翼板结构代替了部分沉箱。梳式防波堤因其梳齿形外观而得名，翼板的位置和长度可以根据不同的工程需要进行设计，其结构见图1。当梳式结构的翼板不直接连接到海床时，部分波浪会通过下方的空洞传入港内，此时的结构称为透空式梳式防波堤。与传统防波堤相比，梳式防波堤造价相对低廉，且具备有效减小波浪反射、减小波浪力、有效吸收波能等特点。大连港大窑湾北部岛堤工程中，成功地采用了一种下部透空的梳式防波堤结构。在以往的研究中，牛恩宗等分析了梳式防波堤的工作机理及掩护效果［7］。董国海、李玉成等通过物理模型试验，对梳式防波堤水力特性进行了系统研究，给出了结构所受波浪力与相关影响参数间的经验公式和波浪反射系数的经验公式［8-9］。张涛等根据物理模型试验中实测的波浪力，对翼板进行了结构内力分析［10］。朱大同研究了梳式防波堤的消防浪特性，给出了一个近似计算波浪反射系数的计算方法［11］。刘子琪等对梳式防波堤上部采用曲线型防浪墙的防浪效果进行了试验研究，结果表明曲线防浪墙阻止越浪效果显著［12］。房卓等通过物理模型试验，对一种非透空梳式防波堤结构的水力学特性进行了研究，对该防波堤的受力机理和工程危险水位进行了分析，并在此基础上提出了改进结构［13］。

梳式防波堤的研究目前处于实验室模型试验阶段，结构组次和波况条件相对有限，缺少对透空式梳式防波堤的透浪特性的相关研究。因此非常有必要建立数值模型，对梳式防波堤的水动力学特性进行更系统深入的研究，为工程设计提供参考。故本文将通过数值方法对此问题进行探讨，并对透空式梳式防波堤结构的透浪特性进行研究。

1 控制方程及源造波理论

本文将基于质量源造波方法建立数值波浪水槽［14］。数值波浪水槽的控制方程为3-D Navier-Stokes方程，其张量表达式如下

式中：i，j=1，2，3；ui为第i方向上的速度分量；ρ为流体密度；p为流体压力；gi为第i方向上的重力加速度分量；τij为粘性应力张量。对于牛顿流体，τij=2μσij，其中μ为水分子粘性系数；σij为平均应变张量，定义为σij=（∂ui/∂xj+∂uj/∂xi）/2。

在源造波方法中，将连续方程（1）在源域内进行修改，修改后的迪卡尔形式为

式（3）中源项可由下式得到

式中：s（x，y，z）为源域内的非零源函数；u（x，t）为波浪水质点的水平速度；dx 为水槽长度方向（x 方向）的网格长度。

在水槽的两端分别设置阻尼层用于吸收波能，消除波浪反射。在阻尼层中，动量方程为

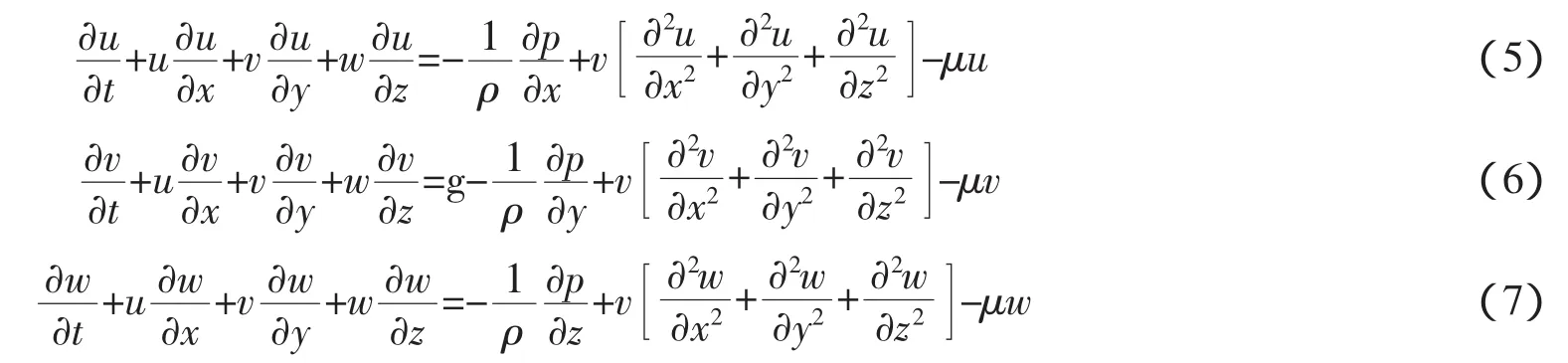
μ为阻尼系数，其取值为

式中：x0为阻尼层的起始点；s为阻尼层的长度，计算中s取两倍的入射波长。

计算域水平长度为60 m（x方向），高度为2 m（y方向），宽度为1.18 m（z方向）。网格在自由水面附近加密，水槽上部与大气相连通，水槽底面采用光滑壁面条件，其他各个壁面都采用对称边界条件。x方向0点设在水槽端部，造波源设在水槽的中部x=30 m处，使波浪向两侧传播。水槽两侧设有阻尼层，长5 m，宽1.18 m，高度为静水面高度。在水槽中设有7个波浪探针，用于实时监测波浪高度。

VOF方法被用来追踪自由表面。计算域内的体积单元由空气和水体2种介质组成。气液两相界面通过求解体积函数F的连续方程得到。压力场和速度场相互耦合，利用压力隐式的分裂算子格式（PISO）求解。在计算体积函数F时，采用了修正的高分辨率界面捕捉方法（Modified HRIC）进行求解，以保证气液两相界面的精确度。动量方程的离散采用了二阶迎风格式。整个数值水槽计算域采用385 990个正六面体单元进行计算，并将网格在自由表面附近处进行局部加密。

2 数值波浪水槽的建立及验证

理论上，只要造波源函数定义正确，任何形式的波形都可以利用源造波法生成。首先，对常水深下的微幅线性波浪进行模拟。采用基于线性波浪理论的源函数生成微幅波，造波源函数形式如下

式中：H为目标波浪的波高；k为波数；d为水深；ω为波浪圆频率。本节中取d=0.7 m，H=0.11 m，ω=4.62。

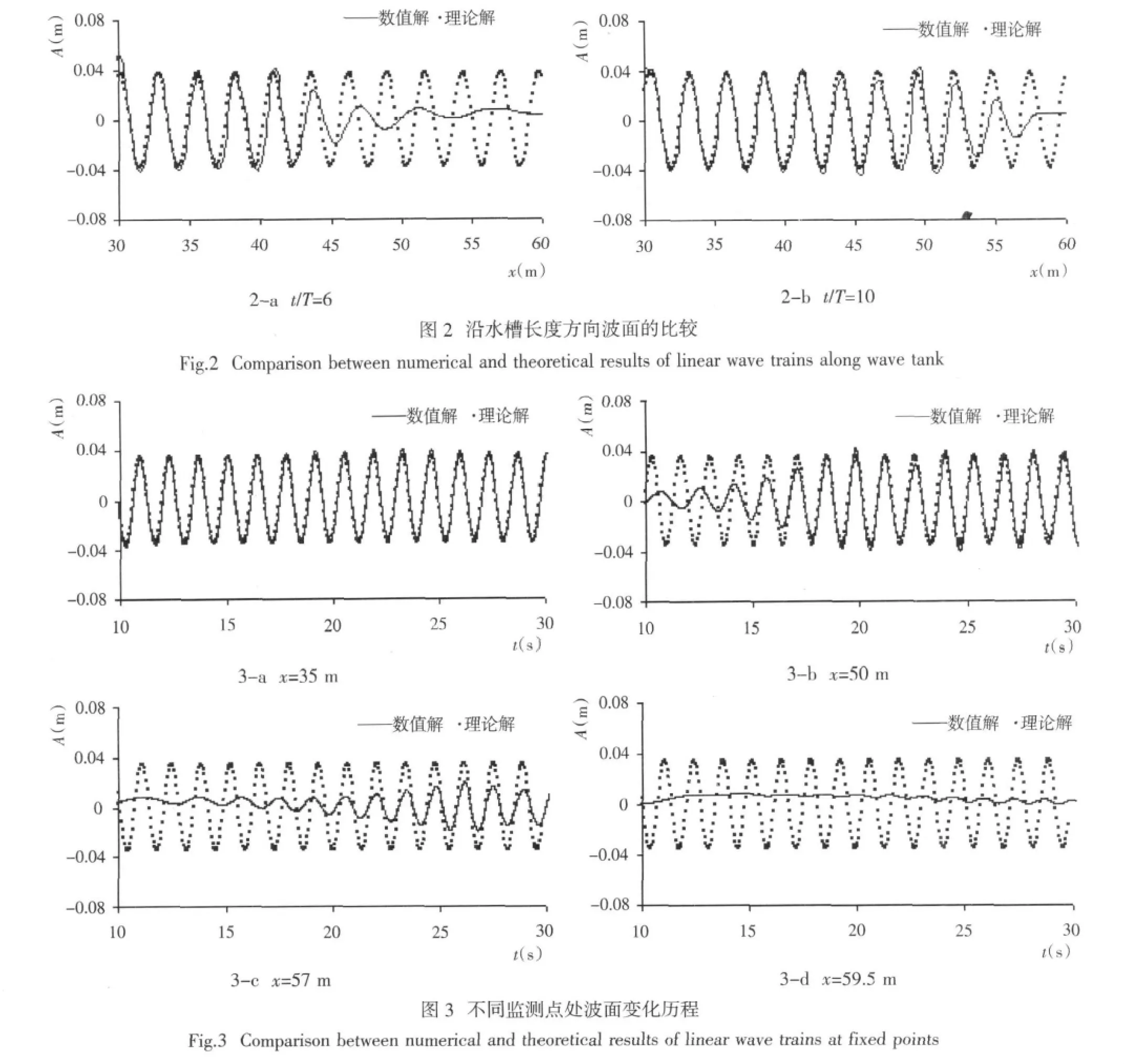
数值模拟结果见图2和图3。图2-a和2-b为t/T=6和t/T=10时波面形状的数值解与理论解的比较；图3-a和3-b中列出了在x=35 m和x=50 m处测得的波面时间历程曲线，结果表明波列沿水槽长度方向传播良好；图3-c和图3-d为阻尼层中的x=57 m和x=59.5 m波面情况。在阻尼层中，波浪能量被逐渐吸收，波高逐渐减小。经计算，波浪通过阻尼层传播到水槽末段时，只剩下约0.1%的波浪能量，说明阻尼层的消波效果较好。

接下来对常水深下的二阶Stokes波进行数值模拟。二阶Stokes波可以分解为由两列波高、频率和初始相位均不同的线性波浪叠加而成，其源函数可以表示为

生成的目标波浪波高为H=0.08 m，ω=5.46，d=0.52 m。图4比较了固定点x=35 m和x=50 m处的波高历程的数值结果和理论结果，可以看到两者符合较好。

不规则波浪可以看成由一系列频率不同、波高各异的线性波浪叠加而成，本文采用JONSWAP谱产生随机波浪［15］，其相应的源函数可以表示为

本文计算了一组由200个波浪模态组成的随机波浪，周期范围为0.5～2.2 s，特征周期为1.39 s，水槽静水深0.52 m，特征波高为H1/3=0.035 m。图5为在水槽x=50 m处测得的波面时间历程，图6为该测点处生成的波浪谱和靶谱的比较，两者结果符合得很好。

从以上各种波形的比较结果可以看到，本文数值波浪水槽可以精确模拟出线性波浪、Stokes二阶波浪及不规则波浪，阻尼层的消波效果也很好。因此将利用本模型继续开展研究，模拟波浪和梳式防波堤的相互作用。

3 波浪与梳式防波堤相互作用的模拟

图7为梳式防波堤的一个结构单元，每个单元包括矩形沉箱、两侧翼板和胸墙3部分结构。2个翼板分别位于矩形沉箱主体的两侧，胸墙位于沉箱的顶部。结构的主要尺寸参数有A，a，b和c。当参数c不为0时，水流和波浪则可以通过翼板下方的开口进入港内。

李玉成等在大连理工大学海岸和近海工程实验室，对梳式防波堤进行了物理模型试验研究［9］。从三百多组试验数据当中，归纳出了防波堤水平波浪力折减系数的经验公式KF和堤前反射系数经验公式KR。KF为梳式结构与实体直墙结构相比的单宽水平波浪力折减系数，即当波峰传至防波堤时，梳式防波堤上与相同尺寸直墙防波堤上最大单宽水平波浪力的比值。本文定义KF-R和KF-IR分别为规则波和不规则波作用在梳式防波堤上时的最大单宽水平波浪力的折减系数；KR定义为梳式防波堤的堤前反射系数。试验结果表明，KF与尺寸参数gT2/A，a/A，b/L，c/d和H/d具有明显的线性关系；不规则波的平均周期与规则波的周期相同且不规则波的H1%与规则波波高相同时，KF-IR小于KF-R，且KF-IR与KF-R比值的统计平均值为0.72，即不规则波作用时有更大的波浪力折减。KR主要与翼板位置b与波长L之比b/L有关。其经验公式关系表达式分别见式（12）、（13）和（14）。

式中：g，A，d，T，a，b，c，L 和 H 分别为重力加速度、沉箱长度、水深、波浪周期、翼板长度、翼板与前墙的距离、翼板下缘高度和波高。在本研究中，数值模型比尺为1：27，各参数的取值为A=0.37 m，a=0.22 m，b=0.22 m，c=0.22 m，c1=0.48 m和c2=0.17 m。

本节将分别对规则波浪和不规则波浪与梳式防波堤的相互作用进行数值模拟。应用二阶Stokes波理论生成规则波浪，波浪条件与上文中用于验证水槽时的情况相同；应用JONSWAP谱生成不规则波浪，不规则波的平均周期与规则波的周期相同，且不规则波的H1%与规则波波高相同，除了防波堤结构表面为壁面条件外，水槽模型的边界条件与上文相同；结构置于x=50 m处，源域与防波堤前墙之间距离为20 m。整个模型采用了387 498个结构化的六面体单元进行计算。

通过数值计算可得规则波浪作用下梳式防波堤上的最大总水平波浪力FC-R，不规则波浪作用下梳式防波堤上的最大总水平波浪力FC-IR和直墙上的最大水平波浪力FV。并进一步求得规则波浪作用下梳式防波堤的水平波浪力折减系数KF-R和不规则波浪作用下梳式防波堤的水平波浪力折减系数KF-IR。应用Goda两点法［16］计算反射率，通过x=46.1 m和x=46.5 m处采集的波面时间序列值，进行入、反射波分离，求得结构的反射系数KR。表1中列出了数值计算与经验公式的结果比较，可见二者符合较好。进一步验证了该数值模型的有效性。

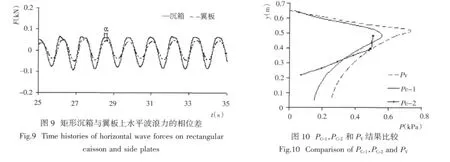
以往的物理模型试验研究表明，梳式防波堤上总水平波浪力的减小主要归结为2个原因［9］：其一，由于翼板与沉箱前沿相距距离b，波浪击堤自翼板和自沉箱前沿的反射不同步而有一个相位差，此相位差一方面减少反射率，同时使翼板所受波浪力峰值与沉箱主体前沿所受波浪力峰值有相位差，从而减少所受波浪力最大值；其二，当c不等于0时，翼板下方的空洞形成透浪，部分波能会透过结构传播到港内，透过的波浪在沉箱主体后墙及翼板后侧也产生波浪力，作用在沉箱主体前墙和翼板前侧的波浪力和前述波浪力也会产生相位差，导致作用在防波堤上的总波浪力减小。这一现象可以通过对沉箱主体上与翼板上单位宽度波浪总力的数值计算结果得到验证，图9证明了2组波浪力之间存在一个相位差α，通过计算可以得到此相位差约为入射波浪周期的11%。

表 1 FC-R，FC-IR，KF-R，KF-IR和 KR的结果比较Tab.1 Numerical and empirical results of FC-R，FC-IR，KF-R，KF-IRand KR

将波峰作用时的沉箱上的压强垂直分布PC-1、翼板上的压强垂直分布PC-2以及直墙上的压强垂直分布PV沿墙高度进行比较（图10）。可见在相同高度处的PC-1和PC-2均小于PV。积分后得到的沉箱上的单位宽度波浪力FC-1=0.187 kN/m，与沉箱对应高度的直墙上单位宽度波浪力FV-1=0.243 kN/m，翼板上的单位宽度波浪力FC-2=0.102 kN/m，与翼板对应高度的直墙上单位宽度波浪力FV-2=0.124 kN/m；FC-1比FV-1小约23%，FC-2比FV-2小约18%。结果表明，与传统的直墙结构相比，梳式结构有效减小了防波堤所受水平波浪总力。

4 透空式梳式防波堤波浪透射系数的研究

透空式梳式防波堤是翼板部分透空的一种梳式防波堤形式，根据实际工程需要，通过调节翼板的高度，起到减小波浪力、减小堤前反射和控制透射波高的综合效果。董国海、李玉成等［8-9］的研究表明反射系数主要与参数b/L有关，这是由于梳式防波堤的反射系数主要取决于入射波和反射波的相位关系；同时，以往仅对参数c=6 m（原型尺寸）的透空式的梳式结构进行了相关研究。故本文对透空式梳式防波堤透射系数的基本规律研究主要考虑参数c/d和b/L对透浪系数的影响。文中基于第三节建立起来的波浪与梳式防波堤的作用模型，一共进行了40组数值计算，考虑了不同的参数c/d和b/L对透浪系数的影响，并根据数值结果拟合出一组经验公式，用于计算波浪透空式梳式防波堤的透浪系数。计算所用水深d为0.52 m，波高h为0.08 m，波浪周期T为1.15～1.5 s。翼板至胸墙正面距离b的取值范围为0.22～0.71 m，相应的b/L为0.11～0.37；翼板下方透空的尺寸c范围为0.05～0.35 m，则相应的c/d为0.1～0.7。参数的选取基本上覆盖了工程实际中结构参数的选取范围。

根据数值计算结果，本文通过最小二乘法拟合出了一组关于透浪系数的经验公式，考虑了主要的影响因素，可以直观方便地计算出梳式防波堤后的透浪系数。该公式的相关系数R为0.992，拟合经验公式如下

当b/L一定时，透射系数KT的数值结果随c/d的变化见图11。可见KT随c/d的增加呈明显的线性增加，即随着翼板下部透空部分长度c的增加，防波堤后的透浪量也逐渐增加。当c/d一定时，透射系数KT随b/L的变化见图12，其变化规律呈抛物线形式，当b/L小于0.25时，KT随着b/L的增加而增加，当b/L在0.25附近时透射系数KT得到最大值，该值接近0.3，其后KT随着b/L的增加而减小。由式（15）得到的经验公式结果也同时在图11和图12中显示，可见拟合的经验公式可以很好地反映波浪透射系数的变化，可为工程设计提供参考。

5 结论

本文基于FLUENT软件利用源造波法建立了三维数值波浪水槽，模拟了一系列的波浪形式，并与理论结果进行了比较。利用数值波浪水槽，分别模拟了规则波浪和不规则波浪与梳式防波堤的相互作用。计算得到以下结论：（1）基于FLUENT软件建立3-D数值波浪水槽，并利用源造波法生成了高质量的线性波浪、二阶Stokes波和不规则波；（2）分别对规则波浪和不规则波浪与梳式防波堤的相互作用进行了数值模拟，对梳式防波堤上波浪力的折减系数和堤前反射系数与物理试验结果进行了对比验证，并对波浪力衰减的机理进行了数值验证；（3）通过数值计算，对透空式梳式防波堤的水动力特性进行研究，重点研究了影响透浪系数的因素。透浪系数KT随透空尺寸c/d的增加而线性增加，随尺寸b/L的变化呈抛物曲线变化，当b/L小于0.25时，KT随着b/L的增加而增加，在b/L等于0.25附近取得最大值，然后KT随着b/L的增加而减小。从数值结果中拟合得到一组经验公式，用来计算透空式梳式防波堤的透浪系数。

［1］王永学.无反射造波数值波浪水槽［J］.水动力学研究与进展，1994，19（2）：205-214.

WANG Y X.Numerical Wave Channel with Absorbing Wave-maker［J］.Journal of Hydrodynamics，1994，19（2）：205-214.

［2］李凌，林兆伟，尤云祥，等.基于动量源方法的黏性数值波浪水槽［J］.水动力学研究与进展，2007，22（1）：77-82.

LI L，LIN Z W，YOU Y X，et al.The numerical wave flume of the viscous fluid based on the momentum source method［J］.Journal of Hydrodynamics，2007，22（1）：77-82.

［3］高学平，李昌良，张尚华.复杂结构形式的海堤波浪力及波浪形态的数值模拟［J］.海洋学报，2006，28（1）：139-145.

GAO X P，LI C L，ZHANG S H.Numerical simulation of wave pressures and wave motions on complicated composite seawalls［J］.Acta Oceanologica Sinica，2006，28（1）：139-145.

［4］周勤俊，王本龙，兰雅梅，等.海堤越浪的数值模拟［J］.力学季刊，2005，26（4）：629-633.

ZHOU Q J，WANG B L，LAN Y M，et al.Numerical Simulation of Wave Overtopping over Seawalls［J］.Chinese Quarterly of Mechanics，2005，26（4）：629-633.

［5］刘针，陈志春.大型港口潜堤越浪后港内波况研究［J］.水道港口，2010，31（6）：561-565.

LIU Z，CHEN Z C.Study on Wave Condition of Large Scale Port with Submerged Breakwater［J］.Journal of Waterway and Harbor，2010，31（6）：561-565.

［6］戈龙仔，迟杰，张慈珩.防波堤堤后次生波的试验研究［J］.水道港口，2010，31（3）：204-209.

GE L Z，CHI J，ZHANG C H.Experimental Research on Secondary Wave Height over Breakwater［J］.Journal of Waterway and Harbor，2010，31（3）：204-209.

［7］牛恩宗，邓磊，马德堂.梳式防波堤的试验研究与实施［J］.中国港湾建设，2001（6）：5-8.

NIU E Z，DENG L，MA D T.Experimental Studies and Construction of Comb-type Breakwater［J］.China Harbour Engineering，2001（6）：5-8.

［8］Dong G H，Li Y C，Sun Z C，et al.Interaction Between Waves and A Comb-Type Breakwater［J］.China Ocean Engineering，2003，17（4）：517-526.

［9］李玉成，孙昭晨，徐双全，等.梳式沉箱防波堤的水力学特性［J］.水动力学研究与进展，2002，17（4）：472-482.

LI Y C，SUN Z C，XU S Q，et al.The hydraulic performance of comb-type vertical breakwater［J］.Journal of Hydrodynamics，2002，17（4）：472-482.

［10］张涛，王清湘，赵国藩.梳式沉箱翼缘板设计理论的研究［J］.海洋工程，2002，20（1）：52-56.

ZHANG T，WANG Q X，ZHAO G F.Research of design theory for flange plate of comb-type caisson［J］.The Ocean Engineering，2002，20（1）：52-56.

［11］朱大同.梳式堤波浪反射系数近似计算［C］//左其华，窦希萍.第十三届中国海洋（岸）工程学术讨论会论文集.北京：海洋出版社，2007.

［12］刘子琪，曲淑媛，王振呈.大连大窑湾一期防波堤工程曲线型防浪墙防浪效果的试验研究［J］.中国港湾建设，2005（1）：16-20.

LIU Z Q，QU S Y，WANG Z C.Experiment and Research on Wave Protection Effect of Curving Wave Walls on Phase I of Dayaowan Breakwater in Dalian［J］.China Harbour Engineering，2005（1）：16-20.

［13］房卓，张宁川，曹燕枝，等.波浪与非透空梳式防波堤作用的试验研究［J］.水运工程，2010（8）：1-6.

FANG Z，ZHANG N C，CAO Y Z，et al.Experimental study on interactions between waves and non-open comb-type breakwater［J］.Port&Waterway Engineering，2010（8）：1-6.

［14］Lin P Z，Liu P L F.Internal Wave-Maker for Navier-Stokes Equations Models［J］.Journal of Waterway，Port，Coastal，and Ocean Engineering，1999，125（4）：207-215.

［15］俞聿修.随机波浪及其工程应用［M］.大连：大连理工大学出版社，2000.

［16］李玉成，滕斌.波浪对海上建筑物的作用：2版［M］.北京：海洋出版社，2002.