安全判定两组数据对应成比例的新方法＊

赵 玉，仲 红，易 磊

(安徽大学 计算机科学与技术学院，安徽 合肥 230039)

安全多方计算SMC(Secure Multi-Party Computation)[1]是研究一组互不信任的参与方在保护各自私有输入信息的前提下进行的合作计算问题。计算结束后，各个参与方除了获得计算结果外，不能获得其他任何信息。保护私有信息的计算几何[2]己成为安全多方计算的一个重要分支，其具体定义的模型为：保护私有信息的计算几何问题的研究就是要设计出相应的协议算法，使得相互合作的用户在计算过程中既能使用对方的有关隐私信息(如点、线段、多边形、平面等)，又不可能获得其具体值。迄今为止，如何设计高效而安全的计算几何协议仍是一个极具挑战的研究课题。参考文献[3]中首次提出了一个秘密判定两组数据对应成比例判定协议，并基于该协议解决了空间几何平面与平面之间的相对位置判定问题。本文在前人的研究基础上对此类问题进行了改善，即运用同态加密方案设计一个安全求解两组数据中对应成比例个数协议。并且利用此协议进一步设计出安全求解两组数据对应成比例协议和安全判定空间中两平面的相对位置协议。本研究不但解决了安全判定两组数据对应成比例问题，还解决了空间两平面的相对位置判定问题。它们都是保护私有信息的计算几何的基本问题，同时对于研究安全的空间几何对象相对位置问题有着重要的指导意义。

1 相关知识

1.1 基础知识

引理 1[4]空间两个平面 h1：A1x+B1y+C1z+D1=0和h2：A2x+B2y+C2z+D2=0的相对位置关系判定如下：

(1)相 交⇔A1∶B1∶C1≠A2∶B2∶C2；

1.2 同态加密方案

就目前大多数同态加密方案而言，同态加密方案可以分为乘同态加密方案和加同态加密方案。若加密方案满足 Ek(x)·Ek(y)=Ek(x×y)，则称其为乘同态，如 ElGamal加密方案[5]。 若加密方案满足 Ek(x)·Ek(y)=Ek(x+y)，则称其为加同态，如Paillier加密方案[6]。本文使用的是加同态加密方案，因为加同态加密方案是安全多方计算的基础知识，其加密的基本思想已经被众人所熟知，所以此处不再赘述。

2 安全求解两组数据中对应成比例个数协议

2.1 问题描述

安全求解两组数据中对应成比例个数协议 (下简称协议 1)问题可以描述为：Alice拥有私有数据 X=(x1，x2，…，xn)，Bob 拥有私有数据 Y=(y1，y2，…，yn)，他们希望在不向对方泄露自己的信息时能判断出彼此对应成比例的个数，除此之外，不能得到对方的任何其他信息。

2.2 安全求解两组数据中对应成比例个数协议的设计

协议的主要思想是：首先将两方的n个私有数据各自分解成n-1个私有分量，每个分量中只包含相邻的两个私有数据。然后，对每个分量分别秘密求解，看两方分量中的数据是否对应成比例，如果数据是对应成比例的，则统计数据是对应成比例的变量N+1。这个过程中用到了数据加密技术和同态加密方案。最后，由N的值判定两组数据中对应成比例的个数。协议设计如下：

输入：Alice 拥有私有数据 X=(x1，x2，…，xn)，Bob 拥有私有数据 Y=(y1，y2，…，yn)。

输出：Alice和Bob在不泄露自己信息的情况下安全求解两组数据中对应成比例个数。

(1)Alice构造一个变量N，并使其满足N=0。

(2)for i=1 to n-1时，执行以下步骤：

①Alice 在本地生成 Xi=(xi，xi+1)；

②Bob 在本地生成 Yi=(yi，yi+1)， 并计算 Y′i=(yi-r，yi+1-r)，其中r为 Bob 的随机数，将 Y′i传送给 Alice；

③Alice使用其公钥 Ea加密数据得 Ea(xi)、Ea(-xi+1)、Ea(xi(yi+1-r))及Ea(-xi+1(yi-r))，并将加密后的密文全部传给Bob；

④Bob计算Ui=Ea(xi)rEa(xi(yi+1-r))=Ea(xir+xiyi+1-xir)=Ea(xiyi+1)，Vi=Ea(-xi+1)rEa(-xi+1(yi-r))=Ea(-xi+1r-xi+1yi+xi+1r)=Ea(-xi+1yi)，那么 Si=UiVi=Ea(xiyi+1)Ea(-xi+1yi)=Ea(xiyi+1-xi+1yi)，并将 Si传给 Alice；

⑤ Alice 解 密 Si， 得 Si′=xiyi+1-xi+1yi， 如 果 Si′=0， 则N++；

⑥i++。

(3)Alice将最终的N值告诉Bob。

2.3 协议的安全性与复杂度分析

安全性分析：由于Alice传给Bob的数据都是通过其公钥进行加密的，因此Bob是无法获得Alice的私有数据；而Bob的数据都是通过其自身的随机数加密传给Alice的，所以计算的过程中Alice无法获得Bob的私有数据。协议结束时，虽然Alice知道n-1个Si′=xiyi+1-xi+1yi的方程，但这些方程中含有 n个未知数 yi(i=1，2，......，n)，所以Alice不能由它掌握的数据推出任何关于Bob的信息。因此协议1是安全的。

复杂度分析：协议1的计算复杂度表现在对数据利用同态加密方案进行计算的过程中。所以计算效率较高，协议1的通信代价次数为3n-2次。

3 安全求解两组数据中对应成比例个数协议的应用

3.1 安全判定两组数据对应成比例协议

3.1.1问题描述

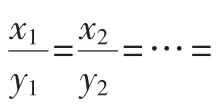
3.1.2安全求解两组数据是否对应成比例协议的设计

协议的主要思想是：首先将两方的n个私有数据执行安全求解两组数据中对应成比例个数协议。最后，由协议的结果N的值判定两组数据是否对应成比例。协议设计如下：

输入 ：Alice 拥有 私 有数 据 X=(x1，x2， … ，xn)，Bob 拥有私有数据 Y=(y1，y2，…，yn)。

输出：Alice和Bob在不泄露自己信息的情况下安全地判定他们是否对应成比例。

(1)Alice和Bob协同执行协议1。

(2)Alice在本地判断N值是否等于n-1，如果N=n-1，两组数据是对应成比例；如果 0≤N＜n-1，则两组数据不对应成比例。

(3)Bob在本地判断N值是否等于n-1，如果N=n-1，两组数据是对应成比例；如果 0≤N＜n-1，则两组数据不对应成比例。

3.2 安全判定空间中两平面的相对位置协议

3.2.1问题描述

空间中两平面相对位置关系判定问题可以描述为：Alice拥有一个平面 h1：A1x+B1y+C1z+D1=0，Bob拥有一个平面h2：A2x+B2y+C2z+D2=0，他们希望在不向对方泄露自己的信息时能判断出这两个平面的相对位置关系。

3.2.2安全判定空间中两平面的相对位置协议的设计

协议的主要思想是：首先将两方各自输入的4个私有数据协同执行安全求解两组数据中对应成比例个数协议。最后，根据引理1的结论，对协议的结果N的值进行比较，从而判定空间中两平面的相对位置关系。协议设计如下：

输入：Alice拥有一个平面 h1：x1X+x2Y+x3Z+x4=0，Bob拥有一个平面 h2：y1X+y2Y+y3Z+y4=0。

输出：Alice和Bob在不泄露自己信息的情况下能安全地判断出这两个平面的相对位置关系。

Alice 在 本 地 构 造 系 数 向 量 X=(x1，x2，x3，x4)；Bob 在本地构 造系数向量 Y=(y1，y2，y3，y4)。 Alice 和 Bob 协同执行协议1，即Alice和Bob在不泄露自己系数向量的情况下能安全地判定他们对应成比例的个数N。

(1)Alice在本地判断，当N=3时，空间中两平面是重合的；当N=2时，空间中两平面是平行的；当N=0或 1时，空间中两平面是相交的。

(2)Bob在本地判断，当N=3时，空间中两平面是重合的；当N=2时，空间中两平面是平行的；当N=0或 1时，空间中两平面是相交的。

本文在已有的研究基础上，设计了一个安全求解两组数据中对应成比例个数协议。并且利用此协议进一步设计出安全求解两组数据对应成比例协议和安全判定空间中两平面的相对位置协议。本协议虽然能很好地解决此类相关问题，提高了协议的效率，并降低了通信量。但是其安全性还有待于进一步的提高，此问题将在以后的工作中进行进一步研究，以设计出更好的协议。

[1]YAO A C. Protocols for secure computations [C].In Proceedingsofthe 23rd AnnualIEEE Symposium on Foundations of Computer Science， Chicago， USA， 1982：160-164.

[2]ATALLAH M J，Du Wenliang. Securemulti-party computational geometry[C]. The 7th Int’l Workshop on Algorithms and Data Structures(WADS 2001)， Providence，Rhode Island， USA， 2001，2125：165-179.

[3]罗永龙，黄刘生.空间几何对象相对位置判定中的私有信息保护[J].计算机研究与发展，2006，43(3)：410-416.

[4]丘维声.解析几何[M].北京：北京大学出版社，1996.

[5]ELGAMAL T.A public key cryptosystem and a signature scheme based on discrete logarithms[J].IEEE Transactions on Information Theory， 1985，31(4)：469-472.

[6]PAILLIER P.Public-key cryptosystems based on composite degree residuosity classes[C].Advances in Cryptology-EUROCRYPT’99， LectureNotesin ComputerScience，Springer-Verlag， 1999，1592：223-238.