基于负熵的多目标射频信号分离研究
2011-05-11林积微周新丰
林积微,周新丰,李 辉
(1.海军后勤技术装备研究所,北京100072;2.中国人民解放军91395部队,北京102443)
0 引言
射频识别技术是一种非接触式自动识别技术,它通过无线射频方式对目标加以识别并交换数据,主要应用于较短时间内在射频区域中识别一个目标[1]。但是在现实应用中,常常需要同时处理在射频工作区域内的多个目标,这些目标可能拥有不同的工作频段、编码方式和传输速率。射频阅读器观测到的信号可能是射频有效区域内,不同类型目标响应读写器发送的信号,经过复杂空间环境的混合信号。
尽管物理上容易实现所有信号的观测,可是传统射频识别技术无法从观测信号中分辨出每一个目标信号,只能通过滤波、防冲突等技术,避免应对多个目标同时识别,这严重降低了射频识别技术的效率、范围,制约了其在多频域、多目标等领域的发展。因此,如何从射频阅读器观测信号中,有效、准确、及时地分辨出目标信号具有重要意义和一定的挑战性。
该文研究采用盲源分离方法中独立分量分析技术,对射频阅读器采集到的信号,建立射频混合信号分离模型,合理应用负熵度量方法,实现射频识别技术中,多目标同时应答混合信号的分离。实验例证和分析表明了射频混合信号分离的可行性和优势。
1 独立分量分析技术
近几年,盲源分离方法研究已经成为数字信号处理领域一个十分引人注目的热点问题,盲源分离的实质是从未知源信号经过未知方法混合的观测信号中重构出原始的各个源信号。对分析者来说源信号通常无法获得任何先验知识,且环境参数同样未知,混合信号是如何混合的也无从知晓。[2]
盲源分离的基本思想就是利用各个源信号之间彼此相互统计独立这一特性建立的,可以通过这个假设条件来弥补源信号先验信息的缺乏。信号盲分离可行的关键是在于要求原始信号之间是彼此相互独立的[3]。独立分量分析(ICA)是一种先进的BSS算法,通过最大化一个基于高阶累积量的分离准则,有的文献也称之为对照函数和目标函数,使得互累积量为零。在此基础上寻找出一个新的矢量坐标系,使得混合信号在该坐标系下的投影元素是相互独立的,并且和原始信号相对应,从而实现信号的分离。[4]
射频信号由不同射频标签响应射频阅读器,经过射频天线发射,并最终被射频阅读器观测。不同的射频信号之间具有良好的不相关性,各个信号本身也具有很强的非高斯型和零均值特征,符合独立分量分析的基本计算前提。而且,有限射频识别区域内,上述射频信号在空间混合过程中,由反射而产生的多路径效应影响很小,空间混合过程符合瞬时混合模型。
2 基于负熵的ICA分离方法
2.1 射频混合信号分离ICA模型建立
首先做出模型的限定性假设:
①假定射频目标应答射频信号可以等效为:S(t)=(s1(t),s2(t),…,sn(t))T是零均值列向量,且在任意时刻各个分量均相互独立;
②从阅读器上所得到的观测信号为:X(t)=(x1(t),x2(t),…,xm(t))T,与射频目标信号数目相等(m=n),则W为实际可实现的n×n阶方阵;
③只容许最多一个射频目标信号的概率密度函数为高斯函数;
④混合过程为瞬时过程,不考虑反射造成多路径而产生的卷积问题;
⑤阅读器中观测电路和各级预处理电路的噪声、失真很小,可以忽略。
射频信号混合ICA的问题模型如图1所示。

图1 自适应射频混合信号ICA方法示意图
观测信号的混合过程表述为:

式中,A为空间混合矩阵。
从ICA的定义可知,ICA的目标就是要估计一个分离矩阵W:

比较理想的情况W就是A-1,恰好可以实现对混合信号的分离,但是所估计的分离矩阵W不能肯定满足方阵并满秩,所以并不一定是A-1。把其中的分离矩阵W称为混合矩阵A的伪逆。
式中,P为一置换阵,I为本单位阵。这就是ICA中模糊性(亦称不确定性)问题:
①分离后的信号顺序是不确定的;
②分离后的信号幅值是不确定的。
另外,通常X和S都是随机过程,假设它们是严格意义上的平稳过程且具有各态历经性,这样可以用时间平均来代替全局期望,保证算法收敛的局部均值具有全局统计特性。
2.2 射频混合信号ICA分离方法
由中心极限定理(任何有限个独立变量源,无论它们的分布如何,在极限条件下,它们的和将构成高斯分布)可以得知,在一定的条件下,相互独立的随机变量的累积和所构成的概率密度分布趋向于高斯分布。在信号模型中,就可以近似的认为,2个相互对立随机变量的和所构成的分布比原始的2个随机变量都要更加接近于高斯分布。
利用2.1节中建立的模型,为了首先估计出其中一个独立成分,对分离矩阵W进行逐行考虑,假设bT为W中的一行,由式(2)可知y=bTx=∑bixi,即估计出的一个独立成分可以表示为xi进行的某种线性组合。进一步可以看到y=bTAs,也就是说分离结果y也是源信号si的某种线性组合,记其系数为q,可知:

理想情况下线性组合bTA就刚好等于一个独立成分,而且对应的向量q只有一个元素为1,其他元素均应为0。
由于2个独立随机变量之和的分布高斯性强于原始各变量,那么y=qTs应该比任何一个si的高斯性更强,除非y刚好是si中的一个,只有在这种情况下y的高斯性才最弱,显然这时q中只有一个非零元素。因此需要通过改变q中的系数,来观察y=qTs的分布变化。
实际中,并不需要得知q的值,由于式(4),同样可以只变化b,并观察bTx分布变化情况,将向量b直接用于极大化bTx的非高斯性,这样的向量对应于q=ATb只有一个非零元素的情形,也就意味着y=bTx=qTs正好成为一个独立成分。综合上述过程,通过极大化bTx的非高斯性,就能分离出一个独立成分。
2.3 用负熵度量非高斯性方法
实际应用中,各类统计值只能从样本中估计,文献[5]总结了负熵引入非高斯性的方法,负熵的概念来自于信息理论中微分熵这个参量,该文将微分熵简称为熵。熵用来描述随机变量的不确定性,变量越随机其熵越大。对于连续型随机变量,概率密度函数为p(x),定义x的微分墒为:

由上述定义可知,熵总是非负的,对于等方差的随机变量,当其满足高斯分布时熵最大(平均功率受限最大熵定理)。这表明,熵可以作为一种非高斯性的度量。
为了合理度量非高斯性,使其对高斯分布取值为零,且始终非负,引入一种熵的标准化版:负熵。可以用负熵来描述一个分布p(x)与高斯分布pG(x)间的差异程度,其中p(x)与pG(x)有相同的均值与方差,负熵的定义如下:
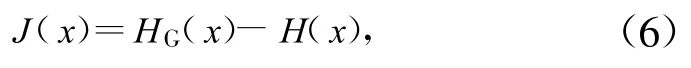
式中,HG(x)表示pG(x)分布的熵。可以分析得到,负熵总是非负的,并且当且仅当x为高斯分布时其值为零。同时它在线性变换下是不变的。负熵作为非高斯性的度量有许多优势,它具有严格的统计性,是度量随机变量非高斯性的最优工具之一。
将高阶累积量近似方法推广,使用一般形式的非二次函数的期望来估计,仅假设2个非二次函数G1和G2,只要满足G1是奇函数而G2是偶函数,可得到如下估计:
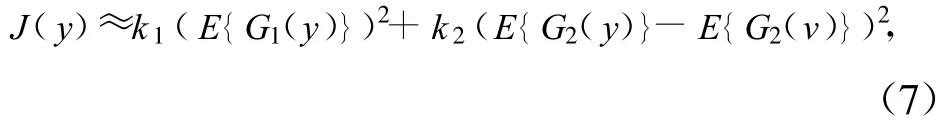
式中,k1和k2是正常数,v是零均值单位方差的高斯变量。变量y也是经过标准化的。如果只使用一个非二次函数G,则可将公式(7)简化近似为:

G可以是任意非二次函数。只要明智合理地选取G,就可以得到较好的负熵近似,特别是选取随自变量增长不是太快的函数,就能得到更好的鲁棒性。根据射频信号非高斯分布特征,选取:

2.3.1 基于负熵的梯度算法
以式(8)定义的负熵近似为基础研究梯度算法,并考虑到标准化过程E{z(wTz)2}=‖w‖=1可以有如下算法:

式中,γ=E{wTz}-E{G(v)},v为标准化的高斯随机变量。函数g是负熵近似中的函数G的导数,参考式(10)。参数γ的引入使得算法具有一种自适应性:

该算法流程如图2所示。
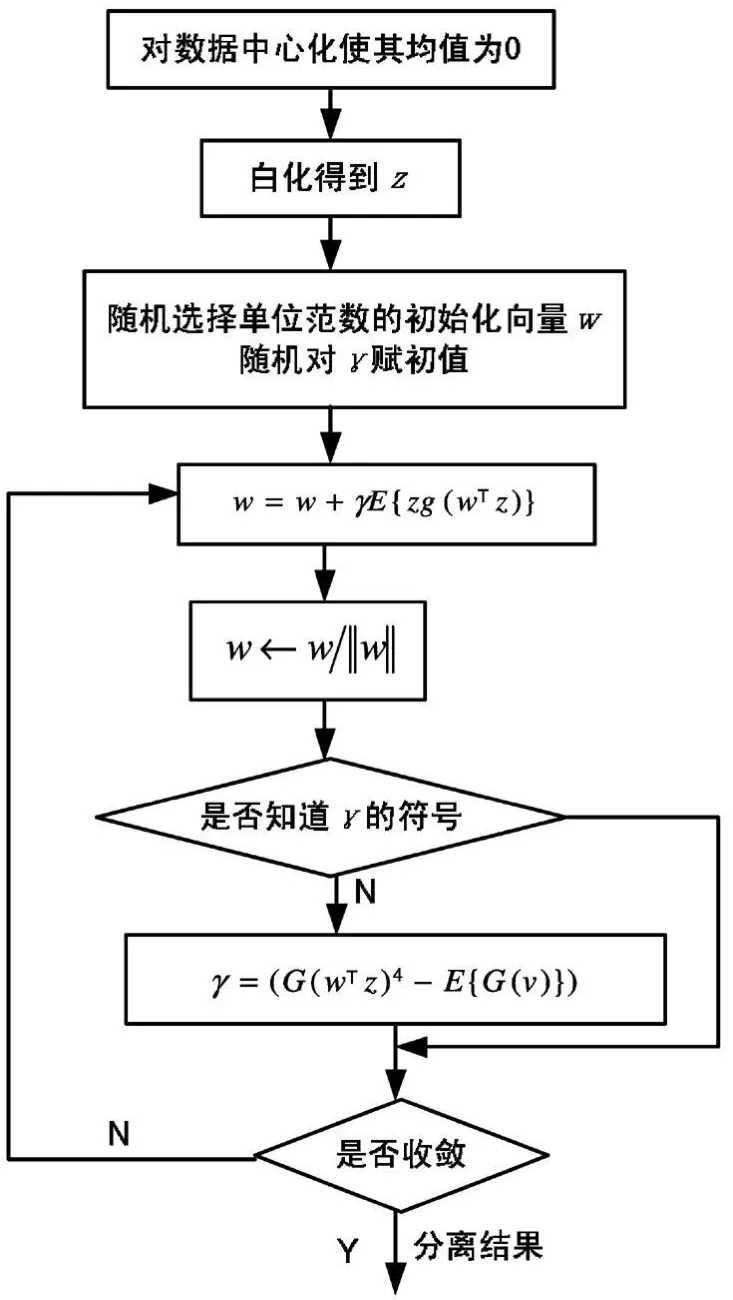
图2 极大化非高斯方向梯度算法流程图
2.3.2 负熵的快速不动点算法
存在着一种不动点法,比梯度法的速度快很多。对应的FastICA算法可以找到一个方向,即一个单位向量w,使得对应的投影wTz的非高斯性达到极大化。非高斯性在这里是利用式(8)定义的负熵近似来度量的。
负熵的FastICA是在不动点不改变的基础上,通过增加额外量改变迭代公式,采用牛顿法寻找拉格朗日乘子式的极值点近似简化得到,具体过程可见参文献[6],得到:

g′(x)为g(x)的导数,算法流程如图3所示。

图3 负熵的FastICA算法流程图
综上可见,基于负熵的FastICA算法有如下特点:首先,收敛速度快,一般依二次方收敛,当独立分量对称时可以达到三次方收敛速度;其次,与梯度算法相比,FastICA算法本身就消除了γ的作用,因此不需要对γ这个参数学习;最后,算法更加灵活,任何非线性函数G都可以按非高斯性最强的要求迭代出独立分量,同时选择适当的非线性函数G之后可以优化算法的性能。
3 试验与结论
3.1 试验准备
为保证定位的精度,采样频率为20GHz,数据长度为20000(即1ms)。选取4组射频信号,分别工作在125kHz、433kHz、13.56MHz、928MHz频率,各个信号采用不同的传输速率和编码方式,详情如实测波形图4所示。试验使用4组射频信号采集设备,各个采集设备观测到的数据如图5所示。
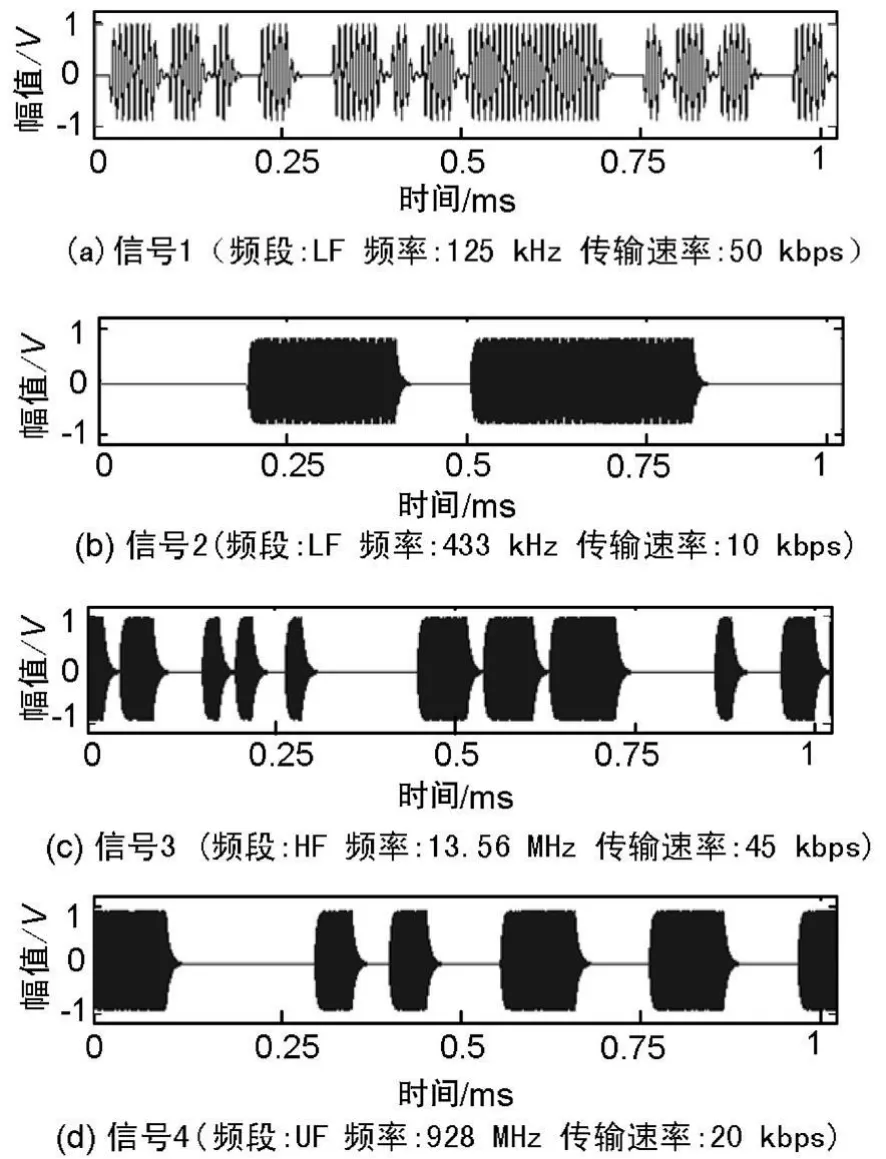
图4 源射频信号实测波形

图5 射频阅读器观测数据组
3.2 试验结果
任意选取随机矩阵W,按照式(9)选取G(y),经过2.3.2节的负熵快速不动点算法流程收敛后得到4个分离信号如图6所示。将图6中依从上到下的顺序,分别称为第1~4个分离信号。

图6 分离得到的各个分离信号
3.3 数据分析及结论
首先,借助测量得到的源射频信号来衡量分离信号的优劣,比较上述图4和图6,并结合上一节中时域内的初步分析,可以看出分离算法已经可以基本实现对混合信号的分离,由于分离算法本身的因素,分离结果在幅值和排列顺序上具有不确定性。
其次,若进一步利用源射频信号与分离后得到的分离信号之间的相关系数可以更加科学地衡量分离的效果。源射频信号si和分离后得到的分离信号yj之间的相关系数为:

理想情况下,当|ρij|≈1时,分离信号j与源射频信号i依概率1线性相关;而其他的|ρij|≈0,分离信号同其他源射频信号统计相互独立,也就意味着分离效果较好。该实验中对应的信号源与分离信号之间的相关系数如表1所示。

表1 多目标射频源信号与分离信号相关系数表
从表1中相关系数指标可以看出,分离算法基本实现了混合信号的分离,其中以分离信号4和分离信号2效果比较好,这也反映出该算法对独立稳定较高频率的信号分离性能比较突出。其次较好的是分离信号1,虽然总体相关性系数不大,但是可以有效地遏制其他成分的影响。从表中可以观察到,分离信号2相关性指标较低,但是比较分离信号2同其他源射频信号的相关系数,仍有一定优势,这表明,在分离过程中能够有效提取独立分量,但是低频信号的总体衰减较大,这也反映了算法对低频高速传输信号的处理能力较弱。
总体上讲,在实验中实现了多目标射频混合信号的分离,获得了一定可信的独立成分。除了算法流程制约外,合理度量选取对分离效率影响较大,同时,系统追求更高的精度就必须以极大的运算量为代价,因而,在精度和运算速度之间必然有所舍取。
4 结束语
采用负熵度量非高斯性的独立分量分析,能够有效地实现多目标射频混合信号的分离,这为拓展射频识别技术另辟了一条蹊径,也为提高射频多目标识别技术的效率和范围奠定一些基础。但由于分离算法的制约、负熵计算中涉及概率密度的估计复杂和严格的环境限定,在现实应用中实现多目标射频混合信号分离任具有广阔的发展空间和一定的挑战性。
[1]FINKENZELLER K.射频识别技术(第3版)[M].吴晓峰,陈大才 译.北京:电子工业出版社,2006:34-36.
[2]林积微.舰艇舱室设备噪声源探测研究[D].武汉:海军工程大学,2007.
[3]张贤达,保铮.盲信号分离[J].电子学报,2007,12A:1767-1771.
[4]徐尚志.盲信号分离算法的研究[D].合肥:中国科学技术大学,2005.
[5]马建仓,牛奕龙,陈海洋.盲信号处理[M].北京:国防工业出版社,2006:85-120.
[6]AAPO H,JUHA K,ERKKI O.Independent Component Analysis[M].USA:John Wiley Sons,Inc,2001:108-165,247-258.
