基于感应电机控制系统的变结构模糊神经网络控制
2011-05-11刘伟
刘 伟
(江苏技术师范学院 电气信息工程学院,常州 213001)
基于感应电机控制系统的变结构模糊神经网络控制
刘 伟
(江苏技术师范学院 电气信息工程学院,常州 213001)
0 引言
交流伺服系统当中的感应电动机是高阶、强耦合、非线性的,由于其参数是时变的、以及在负载干扰等非线性因素的影响下,实际系统很难用其精确的数学模型来描述。而感应电动机以其容量体积比高,过载能力强,输出转矩大,无电刷,无需经常维护等优点而得到越来越多地广泛应用。
交流伺服系统一般是以足够的位置控制精度(定位精度)、位置跟踪精度(位置跟踪误差)和足够的跟踪速度来作为它的主要控制目标。常规的变结构控制以及模糊监督控制都有一个共同的问题,就是“抖振”现象。为了克服这个问题,有人研究过模糊变结构控制[1]。基于感应电动机解耦数学模型而提出的解耦变结构控制原理也是一种新型的交流控制策略[2,3],其解耦变结构控制器的设计方法不需要被控制对象有精确的数学模型,且能有很好的抗干扰性和很强的鲁棒性。如在解耦变结构系统中加入模糊控制,更能有效地抑制和消除抖振,提高控制系统的性能[3]。
模糊神经网络结合了模糊控制与神经网络两者的优势,使控制系统具有模糊推理和自学习、自组织的能力,变结构模糊神经网络通过在训练中不断调整网络结构,一方面提高了网络的收敛速度,找到网络的较佳结构,另一方面又可以有效地克服一般神经网络容易陷入局部值的难题[4]。
1 交流解耦变结构控制
基于对称鼠笼式感应电动机在同步轴系之中的数学模型,可以导出易于实现的解耦条件以及为实现定子侧的完全解耦所需的控制。
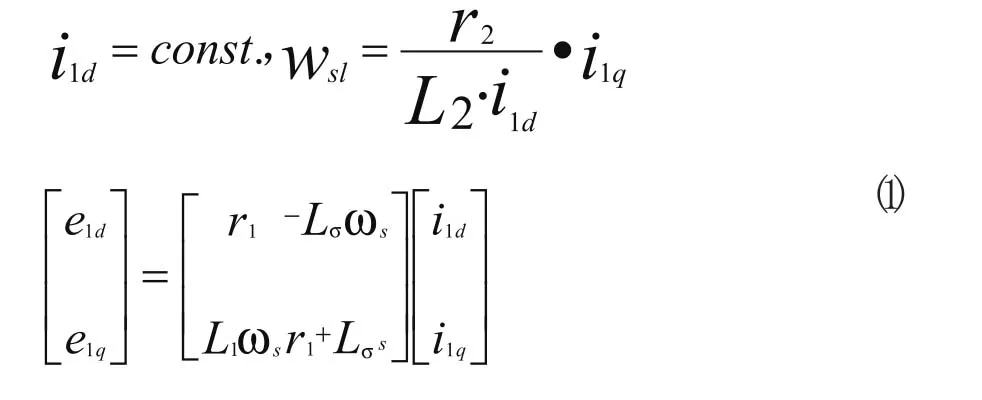
其中,ild,i1q为定子电流的d,q轴分量,ωsl为滑差频率;r1,L1为定子电阻和电感;;r2,L2为转子电阻和电感;Lσ为定转子间漏抗,且Lσ=σL1,σ=1-k2,k为定转子间耦合系数;ωs为电源频率;e1d,e1q分别为电机电势在d,q轴的分量[3,4]。
由于r2容易随温度变化而发生变化,从而影响了解耦控制系统的性能,转子电阻的变化对解耦控制的影响可以作为干扰量h1,h2。感应电动机在完全解耦条件下的数学模型为:


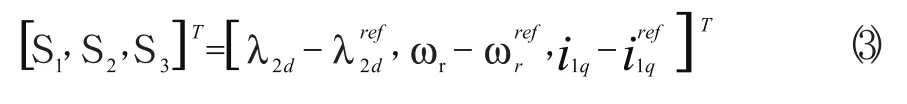
2 变结构模糊神经网络控制
解耦变结构控制策略采用如下的控制规律:

式中,C是控制参数针,uif(i=1,2,3)是模糊控制量。
在采用模糊控制的解耦变结构系统中,采用如下的模糊控制规则:


1)C是正定阵;
2)
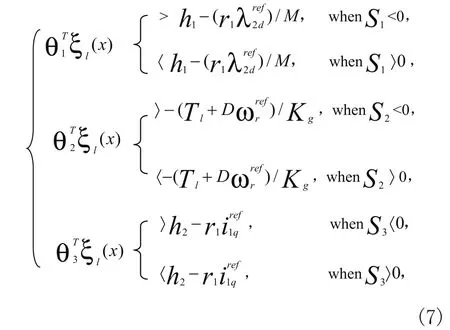
模糊控制采用变结构模糊神经网络来实现,采用变结构模糊神经网络的交流解耦变结构控制系统的结构如图1所示。
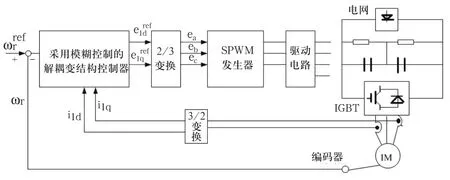
图1 变结构模糊神经网络的交流解耦变结构控制系统的结构图
变结构模糊神经网络控制器结构如图2所示。

图2 变结构模糊神经网络控制器结构图
3 模糊神经网络与模糊规则的调整
变结构模糊神经网络(VS-FNN)控制器是三层前向网络,由于隐层节点数影响神经网络的收敛速度以及神经网络是否收敛于局部极值点,在神经网络学习过程中改变隐层节点的方法,可以提高神经网络的收敛速度,并有效地避免了神经网络陷入局部极值。隐层的节点数由少到多的变结构过程是模糊规则由粗到精的学习过程,体现了先粗略掌握学习对象的概貌,然后不断细分,不断提高学习精度的学习规律,变结构模糊神经网络的结构如图3所示。

图3 变结构模糊神经网络图

对于变结构模糊神经网络(VS-FNN)的隐层,有输入输出方程:
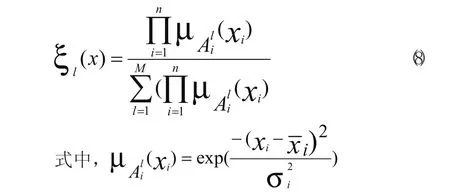
对于比昂模糊神经网络(VS-FNN)的输出层,有输入输出方程:

计算变结构模糊神经网络(VS-FNN)的输出层参数θl的梯度,有:



设ξ为网络输出的误差平方和,D是网络衰减率,则有
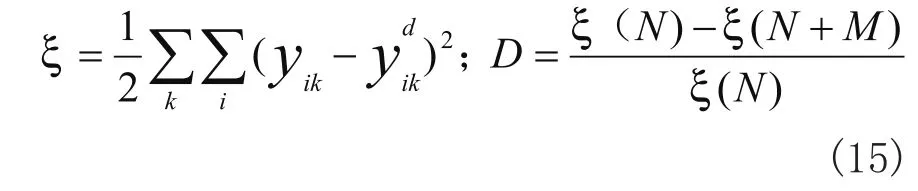
式中,yik,分别是输出层第i个节点的时间输出与期望输出,k为训练样本序号,ξ(N),ξ(N+M)分别是第N步与第(N+M)步训练的误差平方和。设Ep为减去第p个节点后的平方和,则有:

变结构学习算法可归纳为:
第1步 设定ξ>0为给定的误差平方和收敛阀值,[D1,D2]为网络衰减率的适度范围,网络隐层节点数初值为P0。
第2步 设第N步与第(N+M)步训练后的误差平方和与衰减率分别为ξ(N),D(N)与ξ(N+M),D(N+M)。在第(N+M)步稳层结构应为:PN+1
1)假如D(N+M)>D2,表明网络收敛速度快,网络结构保持不变;
2)假如D(N+M) 3)假如D(N+M)∈[D1,D2],网络收敛速度在适度范围,如果D(N+M) 一般改变网络结构会瞬间增大误差,因此新增节点的连接权值应取适当方位的随机值,假如增节点并经M步训练后D(M+N) 本控制系统采用的感应电动机参数:r1=0.49Ω,r2=0.45Ω,L1=38.8mH,L2=36.7mH,M=35.4mH,J=0.024N.m.S2/rad,D=0.0011N.m.S2/rad, i1d=6.83A,i1q=11.54A,P=1KW,U=100V,I=8.4A,W=60Hz,NP=4极,n=1710rpm。 我们采用计算机软件MATLAB对以上感应电动机进行了仿真实验,仿真结果如图4所示。 图4 电机参数为额定值的仿真曲线 图4为电机参数为额定值的仿真曲线,起制动转速ωr在接近最大转矩的作用下快速起动和制动,转速上升时间为0.075s,制动时间仅需0.034s,励磁电流ild上升时间极短,仅为0.009s,达到稳定后基本上保持稳定状态,即励磁基本保持不变。转速ωr除在起制动接近期望值是有短时较小的抖振外,基本上使转速、励磁电流和转矩电流的抖振得到有效地抑制,即使负载突变时转速和励磁电流仍保持不变,说明系统的抗干扰能力较强。 本控制系统具有较高的智能性和很好的鲁棒性,有自学习和自调整模糊规则的能力,系统的动静态性能较好,实现了感应电动机的快速和简单的控制。本文采用变结构模糊神经网络方法,实现了感应电动机的解耦变结构控制,利用神经网络的信息分布存储和并行快速计算能力,实现了模糊控制规则的自动提取和存储,并实现了并行模糊推理,使系统具有模糊控制特性,从而有效地抑制了系统“抖振”的特性。这就是笔者在交流伺服系统中的一种研究尝试,仍有不足之处,如软件实现的模糊神经网络控制,其并行模糊推理的速度会受到影响,在自学习、自组织方面还需进一步完善。仅抛出此方法与同仁们共勉,希望同仁们进一步努力,逐步将新的控制算法付诸于实际系统中,并有更好的实时性。 [1]刘伟.模糊变结构控制在交流伺服系统中的应用[J].电气自动化,2005,27(6):10-12. [2]邱焕耀,毛宗源.采用模糊控制的感应电动机解耦变结构系统的研究[J].自动化学报,1998,24(3):391-394. [3]邱焕耀,毛宗源.感应电动机解耦变结构控制系统抖振和消除的研究[J].自动化学报,1994,20(2):169-176. [4]邱焕耀,毛宗源,姚菁.解耦变结构交流速度控制系统的研究[J].控制理论与应用,1992,9(5):512-518. [5]邱焕耀,毛宗源,姚菁.解耦变结构调速系统的研究[J].冶金自动化,1992,16(5):47-48. [6]王隆杰,毛宗源.利用神经网络进行推理的模糊控制器[J].控制理论与应用,1994,11(4):508-512. [7]Wang Lixing.Adaptive Fuzzy System and Control,Design and Stabd Analysis.London:PTR Prentice Hall,Inc.,1994. According to respond changing of electrical engineering control system structure the misty nerve network control LIU Wei 感应电动机是高阶、强耦合、非线性的被控制对象,它具有容量体积比高,过载能力强,输出转矩大,无电刷,无需经常维护等优点。在感应电动机的控制中采用解耦变结构控制,可有效地简化了控制器的设计,并提高了控制器的抗干扰性和鲁棒性,而在交流解耦变结构系统中进一步应用变结构模糊神经网络,一方面使系统原来存在的抖振现象得以抑制,另一方面又使系统具有自学习和自调整模糊规则的能力,从而提高和改善了控制系统的性能。 变结构模糊神经网络;交流解耦变结构;抖振;学习算法 刘伟(1956 -),男,辽宁锦州人,副教授,主要从事自动控制方面的教学、科研工作。 TP273 A 1009-0134(2011)4(上)-0083-04 10.3969/j.issn.1009-0134.2011.4(上).26 2010-11-12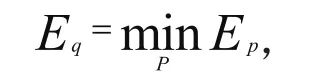
4 仿真及实验结果

5 结论
