一种LEO卫星协同通信系统自适应调制机制与性能分析

晏志勇，刘 芳

（1. 新余学院 机电工程系，新余 338000；2. 新余学院 计算机系，新余 338000）

一种LEO卫星协同通信系统自适应调制机制与性能分析

晏志勇1，刘 芳2

（1. 新余学院 机电工程系，新余 338000；2. 新余学院 计算机系，新余 338000）

0 引言

由于星上系统到地面终端信号传播过程中各种效应的影响,当卫星通信系统的地面移动终端在小仰角工作时,信号的随机衰落甚至超过30dB。随着近年来集成电路设计与实现技术的发展、大功率高频宽带放大器的设计实现,以各种信号处理技术的长足进步,为自适应技术在卫星通信系统中的应用,从而打破传统的固定发射功率、固定码率、确定编码调制方式的卫星通信系统物理层设计与实现方法提供了可能。在自适应调制系统中,一般使地面终端在理想的信道条件下采用较高阶的调制方式,从而在一定的发射功率限制条件下保证接收信号的信噪比,达到保证系统误码性能指标的目的当信道条件恶化时,通过对接收信号的测量感知信道状态的改变,适应性采用较低阶的调制方式,从而在一定的发射功率限制条件下、通过降低信号速率来补偿接收信号信噪比下降对系统误码指标的影响,最终达到保证系统误码性能指标的目的。

参照自适应编码调制技术(Adaptive Coding and Modulation)在UTMS等系统中的成功运用,考虑到未来卫星通信系统星上处理能力(onboard processing-OBP)与终端处理能力的提高,在LEO卫星协同通信系统中,通过对系统信道状态的实时测量,通过一定的信令辅助手段,在信道状态发生改变的情况下,自适应改变编码调制方式,通过改变编码方法、符号传输速率、调制方式、或者扩频码的扩频因子、使卫星通信系统的调制编码方法能够跟随信道状态的变化,在相当大的工作周期比例内逼近信道的山农容量极限,有效保证重要业务的传输,可利用自适应编码调制(Adaptive Coding and Modulation)技术达到充分利用宝贵的卫星无线信道资源的目的。由此,我们提出一种在LEO卫星协同通信系统中根据信道状态改变MQAM调制模式的实现方案,以在特性动态变化的信道中逼近山农信道容量,取得更好的系统性能。

1 LEO卫星通信系统模型设计

图1给出在LEO卫星协同通信系统中实现MQAM自适应调制的原理框图。

地面终端的待传信息经交织、编码等基带处理后,按照系统控制指令选择特定MQAM星座进行MQAM调制,调制信号经滤波、射频调制、与射频放大等处理后经过具有各种衰落和噪声影响的无线信道到达星上接收机。

星上接收端对地面终端发送信息按预先信令约定的调制模式对信号进行解调和译码,输出解调信号。在接收端对接收信号的功率或信噪比进行评估,也可在信号解码后通过对信号误码率的测量对系统信噪比参数进行综合评估。根据对相应信道信噪比的估计结果在假定上、下行信道互惠的情况下、或根据一定关系公式,参照当前信道上所承载的业务误比特率要求,决定相应信道的调制模式并通过信令信道反馈给发送端。同时在下行信道中按照决定的调制模式进行改变。发送端根据星上处理器的决定进行MQAM调制,同时将自身对系统信噪比测试的结果,向星上处理器发送,以供星上处理器用于计算信道状态参数使用。

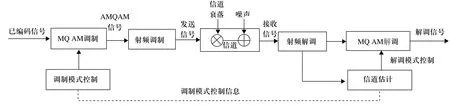
图1 AMQAM原理框图

我们首先在假设信道平稳的前提下假设信道衰落的相干时间大于业务信息包一次传输所需时间周期。即:信道参数变化的速率远低于符号传输速率,信道特性参数在数百个符号传送周期内可近似看作常数,同时假设以上信道状态估计、调制方式同步时间参数和信道估计误差为0。

对于上述的MQAM系统,由于解调器具有M=2n(n=1,2…) 个固定的电平,进行相干解调时,每M进制的错误概率为:

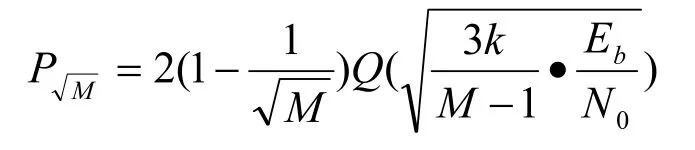
式中:Eb为每比特信号的能量,N0是噪声功率谱密度,n为传输中每个符号携带比特信息量,有n=log2M,M为调制方式的星座点数等。Q (x)是Q函数,可用误差函数erfc (x)表示为:

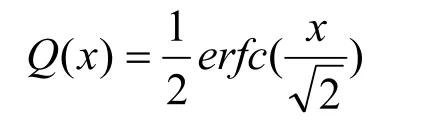
误差函数erfc (x)的定义为:

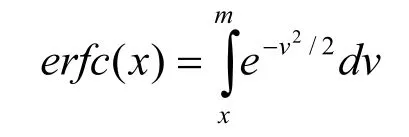
由此得到MQAM误符率为:

由于每个符号携带n bit信息,所以误比特率为:

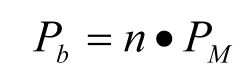
于是有:

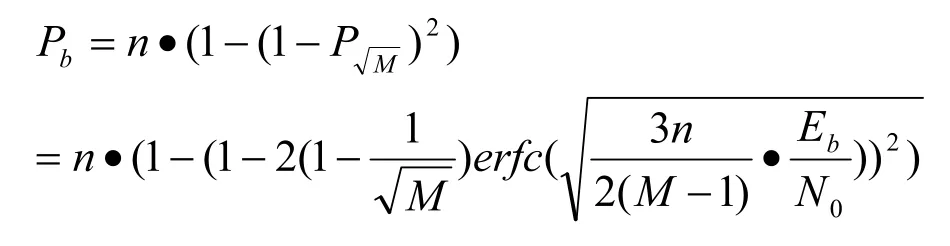
MQAM通信系统的误比特率是信噪比γ=E/N0和MQAM通信系统调制模式M的确定函数。在确定业务n的误比特率Pb≤BERk要求前提下,可求出系统当前信噪比Eb/N0与调制模式n的对应关系。由于物理实现的限制,调制模式M应取2的幂数,即有M=2n(n=1,2…) 。因此,对于某种特定的第k类业务所要求的特定的门限误比特率BERr,可求出针对当前系统信噪比指标γk=Eb/N0所对应的最佳MQAM通信系统调制模式。

假设MQAM系统有种模式可供选择,则AMQAM控制算法可描述为:

算法1(AMQAM控制算法):

1)当γ＜γk1时,根据业务类型k选择什么都不发送(业务暂时中断-非实时连接业务)或选择按最低发送速率的最低调制模式发送(BPSK)。这里γk1代表第k类业务在最低调制模式下保证误比特率门限指标所需的最低信噪比门限;

2)当γkn＜γ＜γk(n+1)时,选择调制模式1≤n≤N。这里γkn代表第k类业务在调制模式n下误比特率门限指标所对应的最低系统信噪比门限。

3)当γ＞γkN时,选择调制模式N。这里γkN代表第k类业务在最高发送速率下选择最高调制模式保证误比特率门限指标所需的最低信噪比门限。

假设话音业务所要求的误码率BERv＜10-3,流媒体业务,交互式业务与后台业务所要求的误码率BERd＜10-6,则可在对应Pev=10-3、Ped=10-6与处各划一条与横轴平行的直线,作为与各业务相对应的BER门限,求出各种调制方式下的SNR-BER曲线与这条直线的交点的SNR值,即可作为各种调制方式在此BER门限下的判决门限。通过Matlab仿真计算得到表1所示结果。

表1 信噪比参数与MQAM模式的选择对照表

2 性能分析

我们已知MQAM系统的归一化频带利用率为:

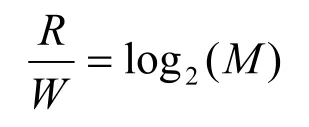
其功率利用率可由误比特率公式来衡量:

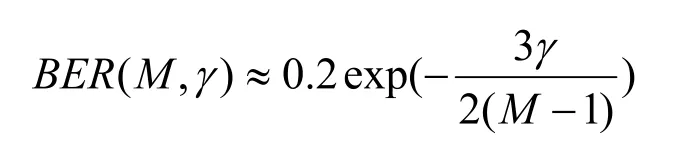
因此,其频带利用率应该用系统在每一个区间的数据速率与系统落在该区域的概率进行加权求和求解,即如果设系统落在以信噪比门限γn表示的区间的概率为Pγ(γ),假设信道条件为缓变平坦衰落信道,信道变化速率远低于符号传输速率,即信道特性在数百个符号传输周期内近似为常数。以Nakagami模型对信道建模,可得:

这里,为接收信噪比的平均值。

则系统在整个工作空间的频谱利用率可表示为:

类似地,由于MQAM自适应调制方法将系统工作模式按系统信噪比情况划分为M个离散的区间,在每个区间内保证实际系统信噪比高于由业务质量要求所对应的系统信噪比门限,因此系统实际工作的误比特率指标通常低于由用户业务质量所要求的目标误比特率指标,为:

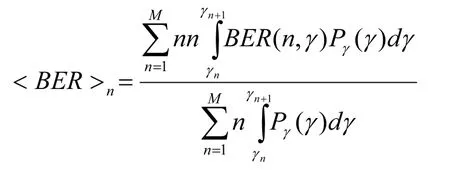
根据以上分析进行数值仿真,可以看到,通过采用自适应方式,使系统容量动态逼近系统信道的动态容量,而对于采用固定模数的QAM系统要么是为了保证系统在90%的分布空间对最苛刻业务的服务质量的保证而浪费了系统的大多数容量,要么就是使相当部分的信道条件下用户业务的服务质量得不到保证。

由仿真结果来看当系统信噪比要求提高时,系统可根据信道状况的改善,改变调制模式,提高星座编码数,以尽可能利用系统信道容量。当系统受各种因素影响导致接收信号信噪比降低时,系统可通过专用信令信道的协调,跟随降低星座编码数,从而在较低的系统信噪比下保证系统的误比特率指标要求。由于数据业务追求更高的误比特率指标要求(数值更低),因此其在相同系统信噪比条件下可达到的系统频带率低于较低误比特率指标要求(数值稍高)的话音业务。由此从另一个角度说明本文所提出的自适应调制方式可在适应信道状况的同时适应业务的变化,达到跨层优化系统性能的目的。

[1]胡小翔, 酆广增. Globalstar卫星通信系统星座模拟和全球覆盖率的研究[J]. 南京邮电大学学报(自然科学版),1998(Z1).

[2]汪小燕, 董燕, 黄载禄. 一种基于地理位置信息的LEO／AdHoc双模网络路由协议[J].微电子学与计算机, 2008,25(2): 67-70.

[3]莫代会, 钱宗峰, 邱敏. LEO卫星通信系统中信道分配策略仿真[J]. 计算机仿真, 2006, 23(5): 33-35, 241.

A LEO satellite coordinated communications system adaptive modulation mechanism and performance analysis

YAN Zhi-yong1, LIU Fang2

我们提出一种在LEO卫星协同通信系统中根据信道状态改变MQAM调制模式的实现方案，以在特性动态变化的信道中逼近山农信道容量，取得更好的系统性能。

LEO卫星协同通信系统；MQAM

晏志勇(1976－),男,江西上高人,讲师,研究方向为机电一体化。

TN914

A

1009-0134(2011)1(上)-0158-03

10.3969/j.issn.1009-0134.2011.1(上).48

2010-09-23