单螺杆大振幅振动对挤出影响的数值模拟研究*

蔡永洪 孙晓辉 黄锋

1 引言

熔体振动技术在聚合物成型加工领域有着广泛的应用，最初应用在热压成型的冷却过程中，可提高制品的力学性能[1]；后来推广到注射成型的保压和冷却过程中，可提高制品的密度和强度，消除熔接痕[2]；还可应用在挤出成型过程中，提高产量，减小挤出胀大[3]。瞿金平发明的电磁式动态塑化挤出机[4]巧妙的运用电磁场使螺杆在转动的同时又有轴向和周向的振动。由于螺杆振动，螺槽内的物料在输送过程中受到振动力场的压实和剪切作用。在进料段和压缩段，振动有助于压实物料，提高熔融速率[5]；在熔体输送段，振动有助于强化层流混合，降低熔体粘度[6]。与传统塑化挤出机相比，电磁式动态塑化挤出机可节能30%～50%，可加工塑料品种更宽[7]。然而，振动强度（频率×振幅）是否越大就越好呢？基于这个问题，本文将对单螺杆大振幅振动对挤出成型的影响进行研究。

与固体输送和熔融塑化两个阶段相比，计量段的熔体输送更直接地影响着挤出机的整机性能。在工程计算中，通常以计量段的输送流率代表挤出机的产量，以计量段的输送功率衡量整机的挤出功率。因此，为了研究单螺杆大振幅振动对挤出成型的影响，本文将重点研究大振幅振动力场对计量段内熔体输送的影响。一个完整的熔体输送理论应该包括二维流场耦合、熔体非牛顿特性、剪切热耗散与热传递、螺槽的几何效应（曲率、终端、侧壁），以及漏流损失。然而，倘若综合考虑以上因素，则难以在数学上取得解析解。为此，通常根据研究重点只考虑其中几个因素而忽略或简化其它的因素，如使用线性本构模型、使用等效（或平均）牛顿粘度[8]、线性叠加拖曳流与压力流[9]；或者借助数值计算方法进行数值模拟[10,11]。

本文综合考虑二维流场耦合、熔体非牛顿特性和剪切热耗散等非线性影响，借助计算流体力学（CFD）专用模拟软件 PolyFlow对单螺杆大振幅振动下的熔体输送过程进行模拟研究。

2 物理模型与数学模型

为了简化物理模型，这里忽略螺杆曲率效应，将螺旋槽展开为平板槽，并在槽末端连接一个楔形收敛口模（H=27mm，d=10mm）。假设平板槽内已完全充满聚合物熔体，对流域内的熔体进行网格划分，如图1所示。平板槽模型的几何参数采用电磁动态塑化挤出机SJDD-260型（转子直径为260mm）螺杆计量段的结构参数，如表1所示。

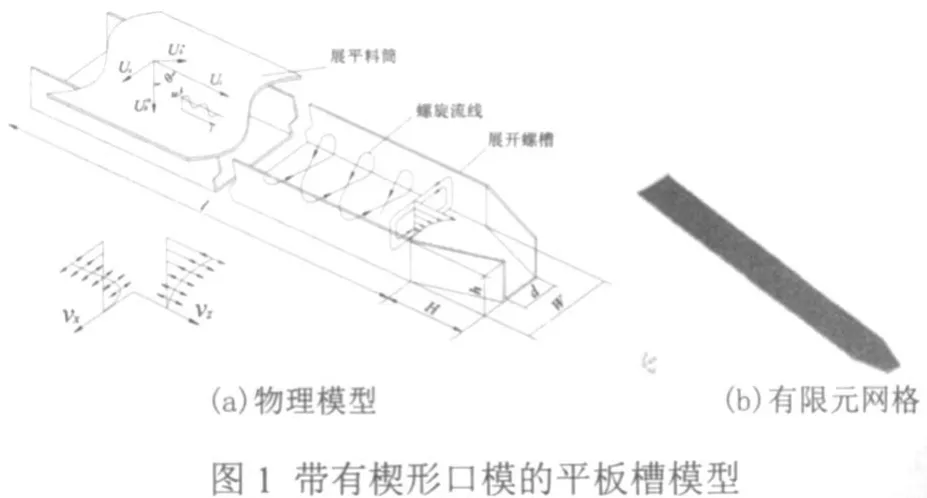
表1 SJDD-260型螺杆计量段的结构参数

为了描述聚合物熔体在螺槽内的粘性流动，选择广义牛顿流体本构方程为：

其中，T是偏应力张量；D是形变速率张量；η是非牛顿流体粘度；γ˙是剪切速率。当考虑二维流场耦合时，剪切速率定义为：

假设聚合物熔体密度为810kg/m3，比热容为2.43 KJ/kg℃，热传导系数为0.24W/m℃，熔体在110℃条件下的粘度方程为：

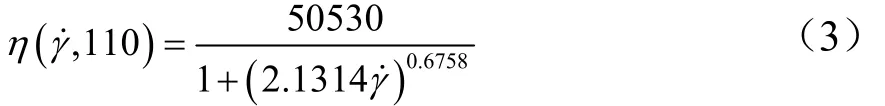
假设粘度对温度满足修正的Arrhenius模型，即：

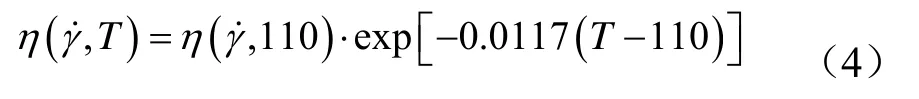
熔体由于料筒的拖曳在螺槽内呈螺旋线型向前脉动输送。当输送达到动态平衡时，料筒温度保持在180℃，螺杆转速设定在 N＝1r/m。为了研究螺杆大振幅振动的影响，固定振动频率为f＝10Hz，分别取振幅 A＝1.5mm、0.9mm、0.6mm、0.3mm进行流动模拟。

为了叙述方便，引入无量纲因子ε：

并定义为振动影响因子。

假设流域内壁面无滑移且螺杆绝热，则移动壁面上的速度边界为：

3 结果与讨论

3.1 瞬态流场分布

图2中实线和虚线分别是振动影响因子ε等于0和0.6（A = 0.9 mm）时流体速度、剪切速率、温度、粘度和压力在半个周期内的沿螺槽分布的曲线。聚合物熔体在拖曳流动时，为了克服螺棱和机头的阻力而粘性增压，产生压力流动。从图2(f)螺槽纵向压力分布曲线可以看出：当t=0.12s时计量段压力差最大。从图2(a)、图2(b)可知：该时刻熔体横向速率很小、纵向速率近似为线性分布，说明熔体做近似纯拖曳流动，即计量段压力差对流场的影响几乎为零。由于其它时刻的纵向压力差更小，因此，本文可忽略纵向压力梯度的影响。这时，横流则成为二维耦合流场非线性分布的主要影响因素。

图2 流变参量的瞬态分布

由于横螺槽方向存在压力反流，所以横向速度分布呈现出抛物线形的压力流特征。这决定了二维耦合流场的剪切速率亦呈相似分布，如图2(c)。因为粘度是剪切速率和温度的函数，在剪切速率大和温度高的地方，熔体粘度低，流动性好。所以根据流场内剪切速率和温度的分布，粘度呈现出中间高两头低的分布特点，即中间层的熔体流动性差，边界层的熔体流动性好。在纵向压力差可忽略的情况下，这种物性差异将直接导致熔体纵向速度分布曲线出现“倒S”形。可见，横流与纵流通过粘度而耦合在一起，相互影响，互为依赖。为了更加清楚的观察到二者的关系，这里对大振幅振动ε=1.0（A=1.5mm）的模拟结果进行论述，如图3所示：当Ux从+Ux,max减小到0时，Uz从Uz,min增大到Uz,0，横流的影响随着Ux的减小而逐渐减弱，纵向速度分布曲线“倒S”形减小。当Ux = 0时，Uz(t)＝Uz,0，横流为零，“倒S”形消失，纵向速度分布近似线性。而当Ux(t)从0继续“减小”到-Ux,min时，Uz(t)则从Uz,0继续增大到Uz,max。这时，横流反向，Ux(t)负向增长，横流影响逐渐增强，导致纵向速度分布曲线“倒S”形增加，以至于下凹部分的熔体速度增长不明显，甚至下降，表现在分布曲线上为下凹部分位于前一时刻曲线之下。

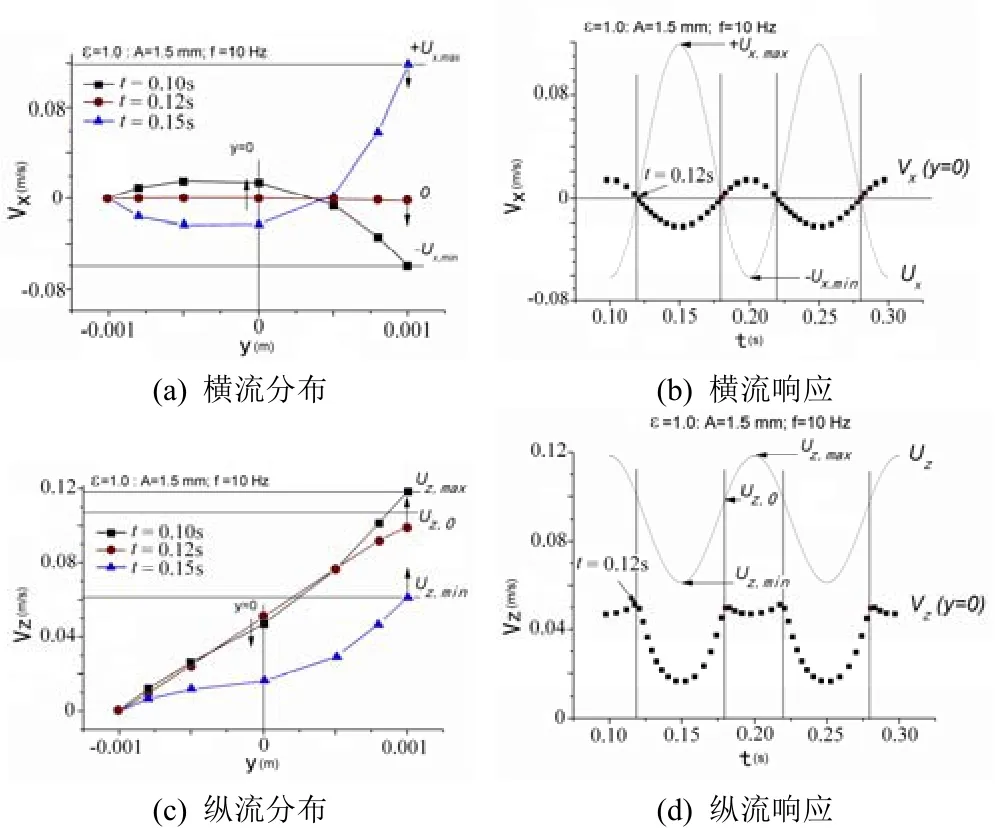
图3 横流与纵流的关系ε=1.0 （f=10Hz, A=1.5mm）

3.2 动态流场响应

图4 所示为y=0, ±0. 5mm三点处的熔体速度在不同振幅下随时间的动态响应。当振动影响因子ε=0.2（A=0.3mm）时，熔体速度在稳态位置（ε=0）处正弦脉动，时均值约等于稳态值；当振幅逐渐增大到一定程度时，如ε=0.6（A=0.9mm）时，波形开始出现返回，并随ε增大而愈加明显。波形的拐点对应于Ux=0时刻。该时刻，横流开始反向流动。正如上文所述，由于横流与纵流相互耦合，在横流影响由强变弱转变为由弱变强时，纵流速度波形产生拐点，波形开始返回。

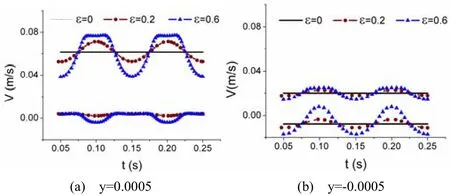
图4 速度随时间的动态响应

图5 所示为振幅对挤出流率的影响。由于流率是纵流的贡献，当纵流出现波形返回时，流率也因此而下降。由图5可知：当振幅A ＞ 0.6 mm时，流率开始急剧下降。图6所示为振幅对挤出功率的影响。显然，振幅越大，熔体输送功耗也越大。然而，当振幅A ＞ 0.6 mm时，功耗急剧增加，产能比严重下降。

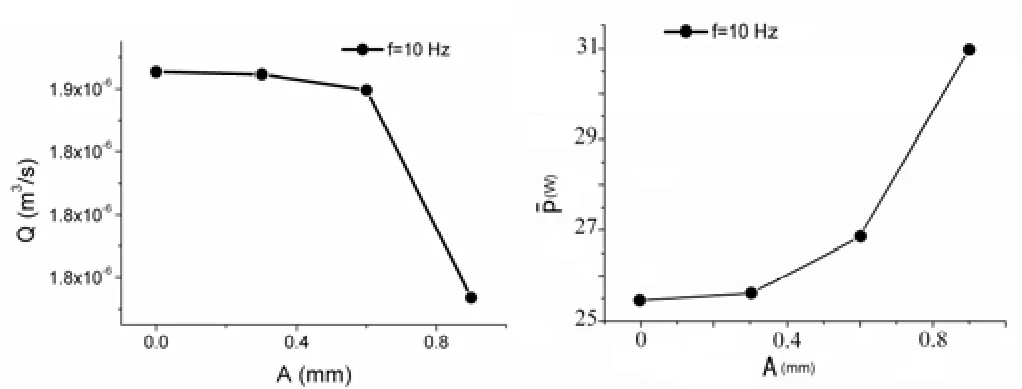
图5 体积流率 图6 功率消耗

为了保持挤出流率和产能比不受损失，应该避免横流反向，即要求Ux(t)≥0。根据式(6)，可得：

即

对于本文，振幅和频率的可选范围如图7中的阴影区域，在该区域之外为横流反向区，即在一个周期内，横流发生反向的区域。

3.3 挤出特性研究

图8是不同振动影响因子下的螺杆特性曲线。当振动参数落入图 7中的横流反向区时，如ε=0.4、ε=0.6，螺杆特性曲线向下偏移，偏移量随振动影响因子增加而增大。这说明落入横流反向区内的振动参数在降低挤出压力的同时也严重的降低了挤出产量，导致螺杆特性变软。

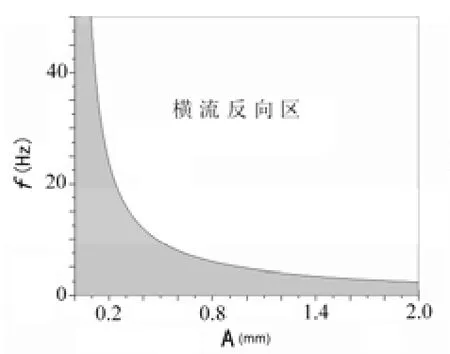
图7 振动参数的可选范围

图8 挤出特性曲线

4 结束语

本文综合考虑二维流场耦合、熔体非牛顿特性、粘性热耗散和热传导，忽略螺杆曲率效应和漏流损失，借助CFD专用模拟软件PolyFlow对广义牛顿流体在带有楔形收敛口模的平板槽内的脉动输送过程进行了数值模拟，得到了熔体速度、温度、粘度和压力等流变参量在平板槽内的瞬态分布，以及不同振幅下的动态响应，研究了大振幅振动力场对熔体输送和螺杆特性的影响。模拟结果显示：振动参数有一个可选范围，当螺杆振动幅值超过该范围而落入横流反向区时，挤出流率将急剧下降，产能比严重降低，螺杆特性变软。

[1] J. P. Ibar. Vibro-Molding. A New Process to Mold Polymeric Materials [J]. ACS Polym. Prep., 1980, 2l (l): 215.

[2] L. R. Shmidt, J. L. Maxam. Injection Molding Polycarbonate Optical Disks Using an Oscillatory Boundary Condition [C].SPE ANTEC Technical Papers, 1992, 38: 447.

[3] J. Casulli, J. R. Clermont, A. Vonziegler, et al. The Oscillating Die. A Useful Concept in Polymer Extrusion [J]. Polym. Eng.Sci., 1990, 30: 1551.

[4] 瞿金平. 电磁动态塑化挤出方法及设备 [P]. CN. Patent: 90 101 034.0, 1990.

[5] 曹建忠, 陈少白. 最优控制在软基预压加固分析与计算中的应用[J]. 自动化与信息工程, 2010, (2): 5-7.

[6] 瞿金平. 聚合物动态塑化成型加工理论与技术 [M]. 北京:科学出版社, 2005.

[7] 吴宏武, 周南桥, 何和智等. 电磁动态塑化挤出机性能的研究 [J]. 中国塑料, 1996, 10 (1): 53-58.

[8] M. L. Booy. The Influence of Non-Newtonian Flow on Effective Viscosity and Channel Efficiency in Screw Pumps[J]. Polym. Eng. Sci., 1981, 21(2): 93-99.

[9] F. W. Kroesser, S. Middleman. The Calculation of Screw Characteristics for the Extrusion of non-Newtonian Melts [J].Polym. Eng. Sci., 1965, 230-234.

[10] R. M. Griffith. Fully Developed Flow in Screw Extruders [J].I&EC Fundamentals, 1962, 1(3): 180-186.

[11] C. Lekakou, J. Brandao. Extrusion of Polypropylene. PartⅡ:Process Analysis of the Metering Zone [J]. Polym. Eng. Sci.,1996, 36(1): 56-63.