大波动短时公路交通流K-近邻预测的稳健组合方法

张 军，王寒凝，杨正瓴，刘正光，叶剑华

(1. 天津大学电气与自动化工程学院，天津 300072；2. 天津市过程检测与控制重点实验室，天津 300072)

K-近邻(K-nearest neighbor，k-NN)非参数回归是公路短时交通流预测的可靠方法之一[1-13]．它是一种无参数、可移植、高预测准确率的算法，其预测误差比较小，且误差分布情况良好．非参数回归预测不需要先验知识，只需足够的历史数据．该算法认为系统所有因素之间的内在联系都蕴涵在历史数据里，因此直接从历史数据中得到信息而不是为历史数据建立一个近似模型．它未将历史数据作平滑处理，因此，较适合在有特殊事件发生时使用[14-15]．从 1991年以来，该方法受到许多短时公路交通流预测研究者的重视，从而得到不断的改进[1-13]．

K-近邻非参数回归预测有4个主要步骤：历史数据准备，样本数据库生成，状态向量定义及 K-近邻搜索，预测算法的确定[3,10]．它在历史数据中搜索出与当前点(模式)最相似的 K个“近邻”，并用这 K个“近邻”预测下一个时段的流量．提高该方法效果的两个主要途径是改进 K-近邻的搜索和改进预测算法(参数调整规则)．

目前，已有的改进工作主要有：采用定点的搜索来提高 K-近邻的搜索；采用结合相关系数[9-10]、模糊理论[4]、聚类[7,11]等方法来提高K-近邻的质量(与当前点相似性)；采用对 K-近邻的调整技术来提高预测效果[1-3]等．但仍然存在搜索量偏大、对波动大的交通流预测效果变差等不足．

在此基础上，笔者用相关系数来替代原来的距离进行K-近邻的选择；采用K-近邻的线性调整技术，结合稳健的组合预测，来改进现有的 K-近邻非参数回归预测，以期达到提高实时性、预测可靠性等效果，特别是改善大波动交通流的预测效果．

1 K-近邻的稳健组合预测方法

1.1 K-近邻非参数回归预测的基本方法

将观察或测量得到的输入-输出时间序列对记为［X ( s), Y ( s )］，s＝1，…，n 是正整数，称它们为学习样本．对于某给定的输入 X ( t)、预测输出 Y ( t) ，K-近邻方法首先按照距离找到最靠近 X ( t)的K个 X ( s)，s＝s1，…，sK．预测结果为

改进 K-近邻预测的 2个主要热点是 K个近邻X( s)的优选以及由 K个 Y ( s)形成预测结果( t)的方法．

1.2 采用相关系数代替距离

现有选择 K个近邻 X ( s)的方法，大多数是以“距离”为标准的．这里的距离，用数学语言讲，就是一种“范数”．最常见的是欧几里德距离(2-范数)．以公路交通流预测为例，X ( s)可以是某些历史的交通流数据，或者是考虑天气、星期等的影响因子．只以距离为选择标准，会有如下4个不足．

(1) 对于波动大的交通流，难以找到高质量的K-近邻．同时需要过长的历史数据，从而使得距离小的各近邻，由于相距时间太久带来的交通流性质变化，不利于提高预测效果，即难以均衡“搜索时间”和“K-近邻的相似性”之间的矛盾．

(2) 采用标准差(方差的开方)进行原始交通流折算，以消除不同天的交通流波动性[1，3]．对于样本容量比较小的 X ( s)，方差估计的置信区间比较长，即标准差计算的真实性不理想．

(3) 距离(范数)只反映当前点和 K-近邻的“靠近性”，不直接反映它们之间的“形状相似性”．而形状相似性则直接反映交通流的变化发展规律．

(4) 为了提高“K-近邻的相似性”，文献[9-10]采用增加相关系数作为评价标准．这样虽然提高了K-近邻的相似性，但是以增大历史数据的搜索(降低实时性)为代价的．

具体的选择方法有聚类[7,11]和平衡二叉树[13]．

本文的改进为：只采用相关系数作为选择 K-近邻的标准．具体方法是将文献[9-10]中的“距离”步骤跳过，只保留相关系数作为评价标准．这样改进的优点有 2个：①相关系数的几何意义是 X ( t)与近邻间“形状的线性相似性”[16]，它直接反映交通流的发展规律，用最大正相关系数选择的各 K-近邻，在交通流的具体数值上可以有很大的差异，从而改善了“大波动”情况下 K-近邻的优选，这样就省去了用标准差折算历史数据的预处理，提高了实时性；②由于相关系数可以将数值差异很大的 K-近邻选择进来，使搜索需要的历史数据量减少，不仅提高了实时性，还提高了 K-近邻间的相似性，即有利于克服交通流性质的长期变化引起的不利影响．

这种方法等效于将每天的交通流标准化：用每天的交通流平均值，对全天交通流折算，消除了“大波动”交通流按照“距离”选择K-近邻的困难．

1.3 采用稳健的组合预测改进预测效果

除了采用式(1)的直接平均外，还可以采用各种先进方法替换式(1)以得到更好的预测效果．现有的方法包括当前模式与近邻间的欧式距离调整[1,12]、相似度调整[13]等．

本文的2类改进是：①采用当前模式和 K-近邻的欧氏距离，调整各K-近邻对应的预测值，这等价于用每天交通流的平均值，再折算回实际的历史交通流数据，它对应组合预测策略中的简单平均法[17-18]；②采用当前模式和 K-近邻的方差，按照组合预测策略中的方差倒数法合成预测的结果[17-18]，具体方法见式(2)．

实际上，各 K-近邻对应的其后交通流，就是待预测交通流的一个预测值．本文采用组合预测策略代替式(1)进行预测，与现有其他改进方法相比较为简单，且预测效果好．

方差倒数法合成 K-近邻预测的具体方法如下所述．本文只采用历史交通流，未考虑其他影响，故Y( s)就是 X ( s)．

记K个近邻 X ( s)对应交通流 Y ( s)在(t+1)点的数值为 y ( t + 1 )，则预测值为

式中：ai是组合预测中的方差倒数法的系数[17-18]，

即组合预测中的简单平均法．进一步，若各 bi＝0，式(3)就退化成式(1)．

2 改进的理论分析

本文改进的主要数学基础是数理统计学[17]和稳健统计学[19]．

当近邻 X ( s)对应的交通流点数不多时，可认为其概率密度函数近似不变(近似平稳的)．这样，无论是欧氏距离、方差，还是相关系数的计算，得到的只是其真实值的“点估计”值，即各统计量的真实值，是分布在该“点估计”值周围的(置信区间)．而置信区间的长度，随着样本容量的增大而明显变小．若记样本容量为 N，则置信区间的长度可以按照1或类似的方式减小．

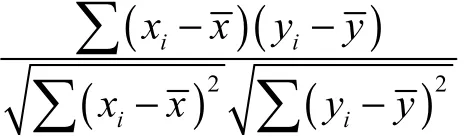
特别地，实际交通流历史数据中总存在一些outliers(离群值、异常数据)，它们使统计量真实值和估计值的差异更明显．增大样本容量、采用统计量的稳健估计方法是改进估计值的 2种有效途径．由于增大样本容量会降低实时性，并增大交通流数据性质变化引起的误差，所以应优先采用稳健估计方法．标准差稳健估计的具体计算方法可参见文献[19]，本文采用的有下面式(4)～(7)．

2.1 采用相关系数代替距离

K-近邻的相关系数选择方法直接解决了各天交通流大波动的不良影响．

(1) 省去了原始交通流数据按每天“标准差”折算的预处理；

(2) 由于平均值估计的置信区间明显比方差估计的置信区间窄[16,19]，从而有效提高了估计的准确性；在下一步的预测中，采用平均值折算预测的效果会得到提高；

(3) 减小了预测必须采用的历史数据量，降低了交通流的长期变化对预测的不利影响．

2.2 采用稳健的组合预测改进预测效果

稳健统计是数理统计学的一个分支，研究当样本数据总体假定稍有变动及记录数据有失误时，统计方法的适应性问题，即主要研究对总体分布的稳健性和对异常数据的稳健性．交通流是复杂时间序列，其“总体分布”是随时间变化的；且交通流含有较高的异常数据(outliers)．采用稳健统计方法，可以明显抑制这些干扰的不利影响[19]．如按照定义计算σ，在 5%的干扰下，计算值会是实际值的 2倍以上．总之，样本容量有限、预测误差的概率分布函数不可知、异常数据这 3种影响因素决定了方差和相关系数在实际工作中不能准确求出．采用稳健统计方法，可显著提高方差和相关系数计算值的真实性．

预测式(2)中需要第i个近邻 X ( si)标准差σ的估计．稳健统计中σ常见的稳健估计方法[19]有

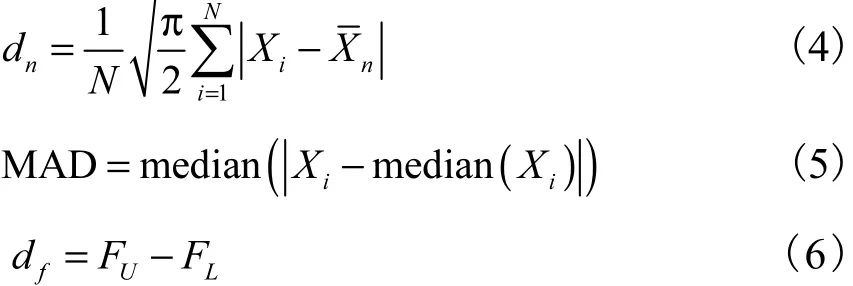
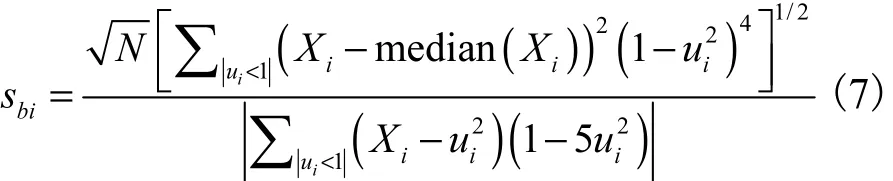
3 示 例

图 1(a)是某公路 33,d的 3,min统计间隔交通流；图 1(b)是按照“每天平均值”折算后的相对值．容易验证，按“每天平均值”折算后的相对值，比采用“标准差”的折算值更平稳．

图 2是该交通流最后 3天的小波周期图．根据时间序列分析中的 Wold分解定理(1938年)和Cramer分解定理(1961年)，交通流可以分解为“复杂的信号(确定的和随机的)+白噪声”．其中的白噪声形成一个目前任何科技方法都不能预测的误差极限．目前还没有可靠的方法来精确分离出白噪声．

从工程角度看，采用小波去噪方法可以近似分离白噪声．这可用于客观地评价某预测方法的效果．

图2 交通流最后3天的小波周期Fig.2 Wavelet transform of the latest 3 days of traffic flow

采用最后 3天每天下午 16：38—19：12(第 0.7～0.8天)共48点的数据作为预测对象．表1为采用小波去噪得到的预测误差极限，即交通流中包含的白噪声引起的预测误差．其中 MPE是平均百分误差(mean percentage error)，MAPE是平均绝对百分误差(mean absolute percentage error)．

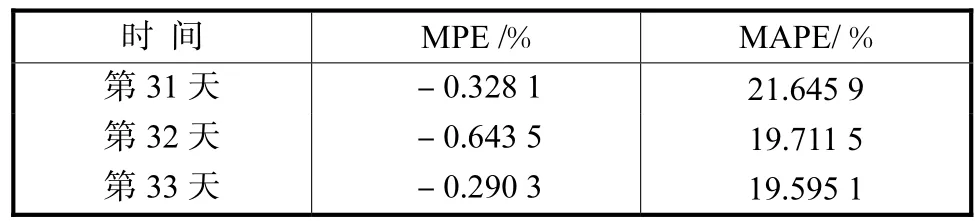
表1 小波去噪得到的预测误差极限Tab.1 Forecasting error limits estimated by wavelet denoise

第31～33天每天上述48点滚动预测采用 X ( s)的样本容量为20，近邻个数 K＝6．采用本文改进方法得到的预测误差见表2．s、dn、MAD、df、sbi依次表示方差倒数法中标准差计算采用的方法，见公式(4)～(7).

可见，由于交通流的波动性、存在离群值，简单平均法和非稳健的方差倒数法 s预测效果不如稳健的方差倒数法 dn、MAD、df、sbi效果好．

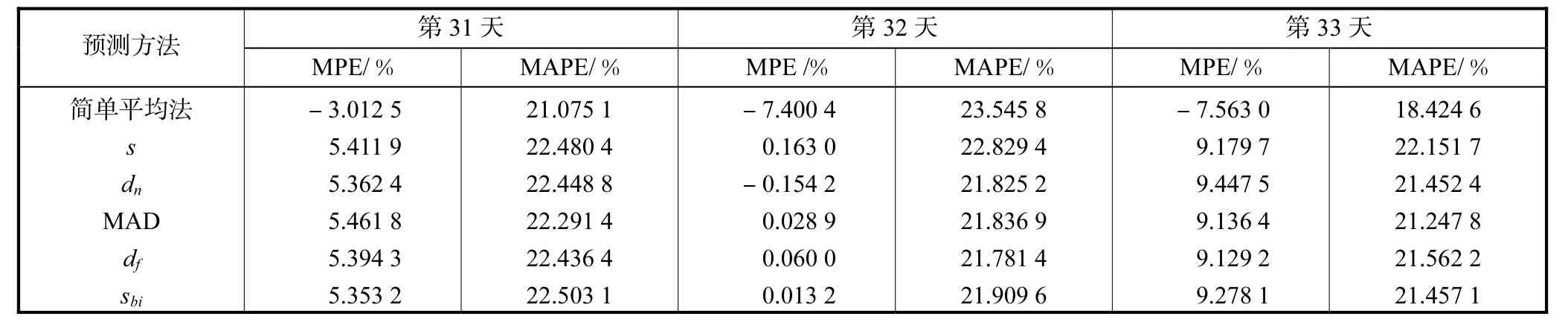
表2 本文方法的预测误差Tab.2 Forecasting errors by the proposed methods in this paper

图 3为第 33天采用 dn进行方差倒数法预测的结果．

可见，预测值的波动比实际交通流小，因为实际交通流里包含白噪声的瞬时值是不能预测的．

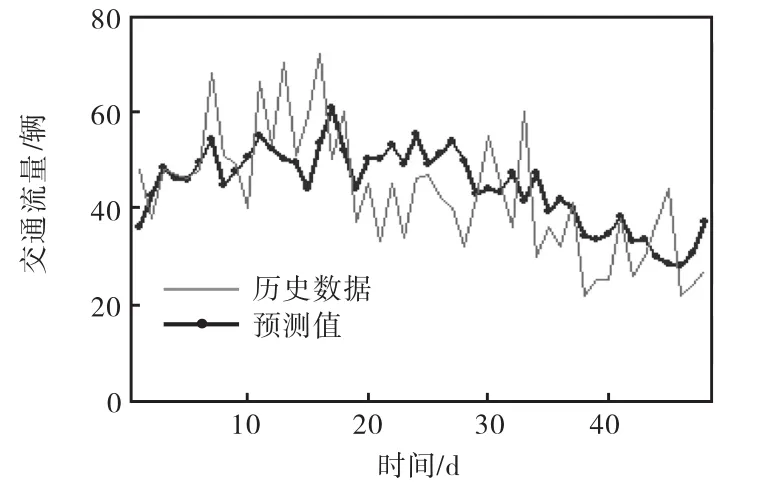
图3 第33.7—33.8天的交通流历史数据与预测值Fig.3 Forecasting data and the original traffic flow Fig. 3 between the 33.7 and the 33.8 days

4 结 语

K-近邻非参数回归预测是一种受到广泛重视的公路短时交通流预测方法．本文对 K-近邻非参数回归预测方法做了如下改进．①直接采用相关系数进行 K-近邻的选择．不仅减少了数据的预处理，还适用于大波动的数据，减少了预测所必须的历史数据．②K个近邻对应的下一点历史数据，调整后就是待预测交通流的 K个预测值．采用组合预测的方差倒数法合成它们，可以得到好的预测结果．③为了降低离群值的不利影响，可以采用稳健统计的方法来计算各标准差的估计值．结果表明，采用稳健统计的方差倒数法，具有较为稳定的预测效果，可以提高预测准确率1%以上．

［1］Turochy R E. Enhancing short-term traffic forecasting with traffic condition information[J].Journal of Transportation Engineering，ASCE，2006，132(6)：469-474.

［2］Smith B L，Williams B M，Oswald R K. Comparison of parametric and nonparametric models for traffic flow forecasting[J].Transportation Research Part C：Emerging Technologies，2002，10(4)：303-321.

［3］Davis G A，Nihan N L. Nonparametric regression and short-term freeway traffic forecasting[J].Journal of Transportation Engineering，1991，117(2)：178-188.

［4］Guo Limei，Luo Dayong. Short-term traffic flow prediction based on nonparametric recursive time series[C]//Proceedings of the Second International Conference on Modelling and Simulation(ICMS2009). Manchester，United Kingdom，2009，6：305-310.

［5］Wang X Y，Juan Z C，Liu M，et al. The application of nonparametric regressive algorithm for short-term traffic flow forecast[C]//Proceedings of the First International Workshop on Education Technology and Computer Science. Wuhan，China，2009，III：767-770.

［6］Zhang Y，Liu Y C. A novel approach to forecast weakly regular traffic status[C]//Proceedings of the11th International IEEE Conference on Intelligent Transportation Systems. Beijing，China，2008：998-1002.

［7］张晓利，贺国光. 考虑交通吸纳点的非参数回归组合型短时交通流预测方法[J]. 系统工程，2006，24(12)：21-25.

Zhang Xiaoli，He Guoguang. The combined forecasting approach based on non-parametric regression for shortterm traffic flow of roads with parking spaces[J].Systems Engineering，2006，24(12)：21-25(in Chinese).

［8］周小鹏，冯 奇，孙立军. 基于最近邻法的短时交通流预测[J]. 同济大学学报：自然科学版，2006，34(11)：1494-1498.Zhou Xiaopeng，Feng Qi，Sun Lijun. Short-term traffic flow forecasting based on nearest neighbor algorithm[J].Journal of Tongji University：Natural Science，2006，34(11)：1494-1498(in Chinese).

［9］宫晓燕，汤淑明. 基于非参数回归的短时交通流量预测与事件检测综合算法[J]. 中国公路学报，2003，16(1)：82-86.

Gong Xiaoyan，Tang Shuming. Integrated traffic flow forecasting and traffic incident detection algorithm based on non-parametric regression[J].China Journal of Highway and Transport，2003，16(1)：82-86(in Chinese).

［10］范鲁明，贺国光. 改进的K近邻非参数回归在短时交通流量预测中的应用[J]. 长沙交通学院学报，2007，23(4)：39-43.

Fan Luming，He Guoguang. ImprovedKnearest neighbor nonparametric regression and its application in short-term traffic flow forecasting[J].Journal of Changsha Communications University，2007，23(4)：39-43(in Chinese).

［11］范鲁明，贺国光. 改进非参数回归在交通流量预测中的应用[J]. 重庆交通大学学报：自然科学版，2008，27(1)：96-99.

Fan Luming，He Guoguang. Application improvement of nonparametric regression to traffic flow forecast[J].Journal of Chongqing Jiaotong University：Natural Sci-ence，2008，27(1)：96-99(in Chinese).

［12］李振龙，张利国，钱海峰. 基于非参数回归的短时交通流预测研究综述[J]. 交通运输工程与信息学报，2008，6(4)：34-39.

Li Zhenlong，Zhang Liguo，Qian Haifeng. Review of the short-term traffic flow forecasting based on the nonparametric regression[J].Journal of Transportation Engineering and Information，2008，6(4)：34-39(in Chinese).

［13］张晓利，贺国光，陆化普. 基于K-邻域非参数回归短时交通流预测方法[J]. 系统工程学报，2009，24(2)：178-183.

Zhang Xiaoli，He Guoguang，Lu Huapu. Short-term traffic flow forecasting based onK-nearest neighbors nonparametric regression[J].Journal of Systems Engineering，2009，24(2)：178-183(in Chinese).

［14］王 进，史其信. 短时交通流预测模型综述[J]. ITS通讯，2005，7(1)：10-13.

Wang Jin，Shi Qixin. A review of the short-term traffic flow prediction methods[J].ITS Communication，2005，7(1)：10-13(in Chinese).

［15］刘 静，关 伟. 交通流预测方法综述[J]. 公路交通科技，2004，21(3)：82-85.

Liu Jing，Guan Wei. A summary of traffic flow forecasting methods [J].Journal of Highway and Transportation Research and Development，2004，21(3)：82-85(in Chinese).

［16］Bernstein R，Bernstein S.Schaum's Outline of Elements of StatisticsⅡ：Inferential Statistics[M]. New York：McGraw-Hill Companies，1999.

［17］唐小我，马永开，曾 勇，等. 现代组合预测和组合投资决策方法及应用[M]. 北京：科学出版社，2003.Tang Xiaowo，Ma Yongkai，Zeng Yong，et al.Modern

Combination Forecasting and Investment Decision Approach and Applications[M]. Beijing：Science Press，2003(in Chinese).

［18］De Gooijer J G，Hyndman R J. 25 years of time series forecasting[J].International Journal of Forecasting，2006，22(3)：443-473.

［19］Hoaglin D C，Mosteller F，Tukey J W. 探索性数据分析[M]. 陈忠琏，郭德媛，译. 北京：中国统计出版社，1998.

Hoaglin D C，Mosteller F，Tukey J W.Understanding Robust and Exploratory Data Analysis[M]. Chen Zhonglian，Guo Deyuan，Trans. Beijing：China Statistics Press，1998(in Chinese).