基于电磁拓扑理论的场线耦合分析与仿真

柳海明，王国栋

(北京交通大学 电 子信息工程学院，北京 1 00044)

我国电气化铁道发展迅速，动车组、磁悬浮列车等把轨道运输能力提升到极限速度，列车电磁兼容性安全越来越引人瞩目。基于多导体传输线理论的BLT方程[1]，旨在解决由电缆组成的复杂网络中干扰电压源和电流源在终端负载引起的响应。扩展的BLT方程[2]，则在经典BLT方程的基础上加入了辐射电磁场对线路的耦合，从而引起终端负载产生干扰响应。本文通过一个场线耦合的实例进行建模，运用传输线理论，依据原始BLT方程的推导方法，重新推导了该模型下BLT方程的表达形式。运用扩展的BLT方程求解电磁脉冲在负载端的干扰情况，并与运用数值仿真软件得到的结果进行对比，证明了扩展的BLT方程的实用性。

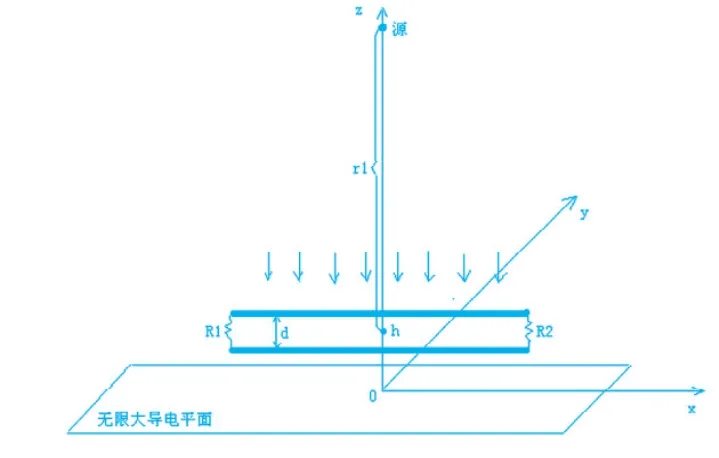
图1 场线耦合模型

1 场线耦合模型

参考前人在这方面的研究模型[3]，考察如图1所示的平行双线，端接终端阻抗为R1,R2的负载在强电磁脉冲作用下的瞬态响应。平行双线传输线的导线半径r，长度L，线间距为d，且平行于无限大的导电平面。传输线中线距离地面高度为h，源距离传输线的距离为r1。

为简化模型，便于理论分析，首先做如下的假设：（1）任何源、传输线、地平面以及场观测点之间的距离相对于波长来说必须足够大，以满足运用辐射和散射场的远场公式；（2）传输线的长度L与波长具有可比性，因此传输线必须考虑长线情况；（3）传输线位于无限大导电平面附近以消除传输线的天线模式响应，即共模电流的影响，只分析传输线模式电流。

基于电磁拓扑的理论，用节点来表示负载、场观测点及感兴趣（或待考察）的位置（如场与路的耦合节点），用管道来表示传输线或假想的电磁场传输通道，可以将场与路的关系用等效的电路结构来表示，如图2。

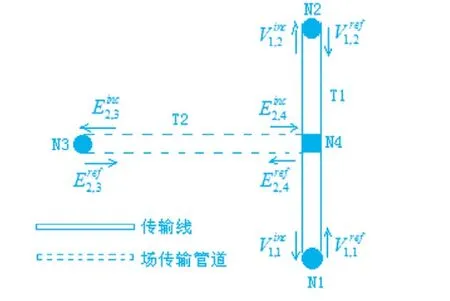
图2 拓扑结构流图

2 场线藕合模型BLT方程的建立

首先考虑图2在自由空间的情况，即不存在无限大导电平面时，对于节点1和2，可以得到方程

考虑到激励源在传输线处为入射平面波的情况，根据文献[3]可得

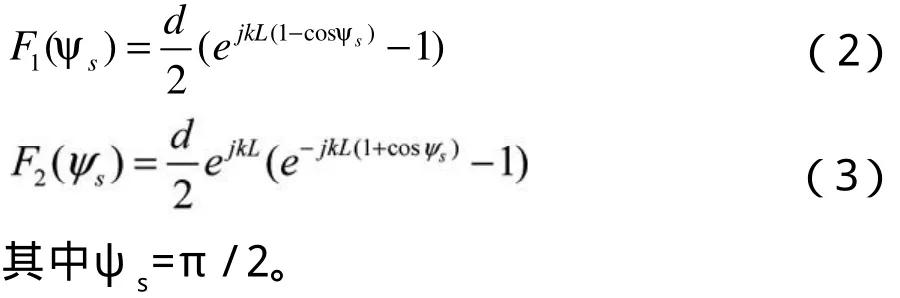
如果传输线附近存在无限大导电地平面，考虑到地面反射的影响，将其叠加到方程中，联系地面反射场和入射场的关系，有：

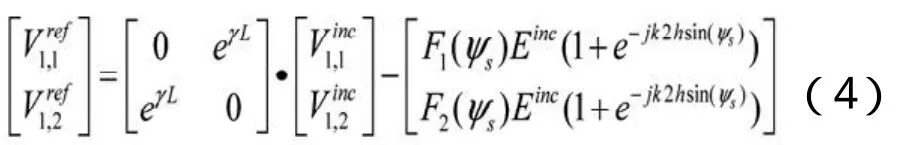
如果激励源为极小电流元的情况，忽略极化效应并保证满足远场条件的情况下，

其中，

第1项表示直接入射到传输线的影响，第2项代表了经由地面反射后到达传输线的波，方向为-k方向。在（5）式中，因为在N3处不存在散射体，因而无反射，即0 。为表达式完整起见，先保留此项。

源可以用偶极子天线产生，其极小电流元可表示为：

同样的方法来考虑管道2的情况，可得到类似的方程。其中需要加入镜像传输线对管道2的影响，有：

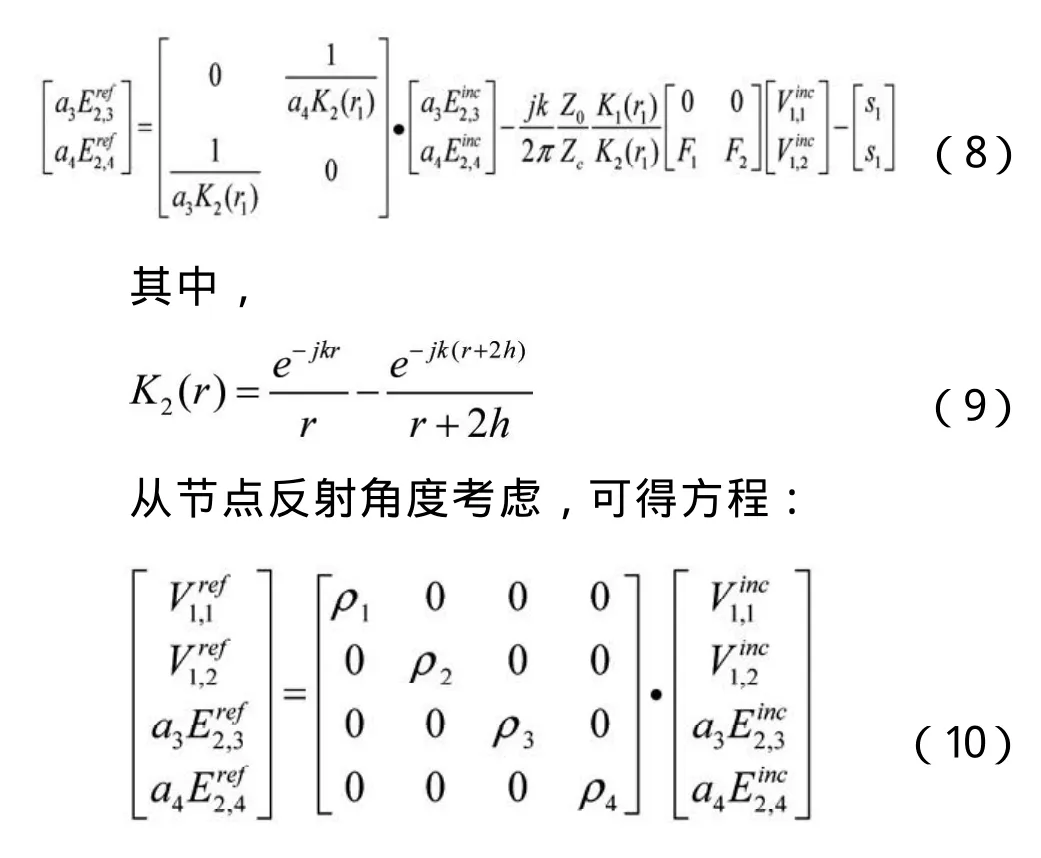
其中，ρ1到ρ4为各个节点的电压反射系数。ρ1、ρ2可以用负载阻抗与特征阻抗的关系式求得，而这里的ρ3=0，因为在该点处无反射，ρ4可以根据文献[4]知：

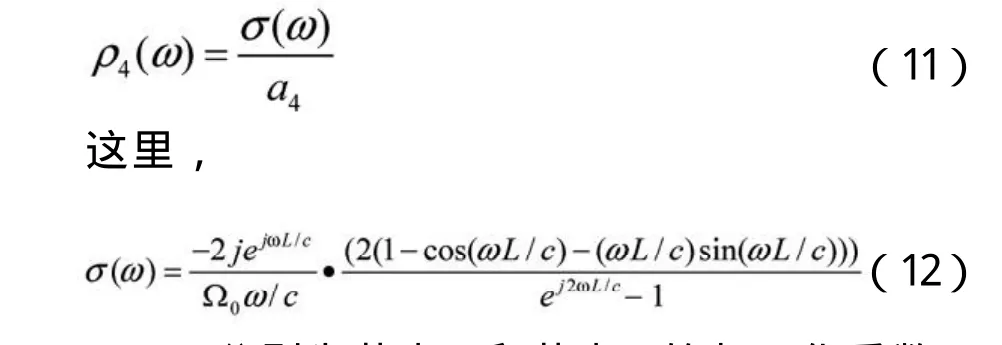
a3、a4分别为节点3和节点4的归一化系数，主要作用是将该点处的场强转化为对应的电压便于进行比较，

数值与该节点的几何尺寸和形状有关。

综合以上各式，整理可得：

图3 激励源作用下的负载响应的时域波形

3 数值仿真计算及分析

考虑在如下几何尺寸：传输线长度L=1m，线间隔距离d=1cm，线半径a=1mm，特征阻抗取Zc=120 ln(d/a)=276.3Ω，负载阻抗取ZL=Zc/2=138.15Ω，传输线与地平面的高度为h=3 m，源与线的间距r1=10m，源与场观测点的距离r2=10m。分别考虑在双指数脉冲干扰和高斯脉冲干扰信号作为源的情况下，电缆两端负载受干扰的强度。下面分别用双指数脉冲干扰和高斯脉冲干扰信号为源，来计算平行双线上负载端的电磁响应。

3.1 双指数脉冲干扰信号

高空核电磁脉冲是一种常见的空间电磁干扰类型，其瞬间发射的电磁波具有双指数脉冲函数的形式，具有场强大、频谱宽、作用范围广的特点，对电力电子系统有很大的危险。这里极小电流源选取为双指数函数脉冲形式，

当在单位激励(I(f)dl=1)作用下，带入BLT方程可得节点1、2出的负载响应电压，即可求出电压传输函数频谱。在双指数脉冲函数激励下的负载响应，可用双指数脉冲函数频谱乘以传输函数即可得到其频域形式，要得到时域的干扰波形，只需再进行FFT逆变换即可。负载处时域响应波形如图3。

从图3中可以看出激励脉冲在负载2处产生的响应主要有2次，第1次在第33.6 ns时刻，第2次在53.6 ns处。2次脉冲响应时间上相差20 ns。这是与理论分析结果一致的。入射电磁波分别在直射和经地面反射2次作用于传输线上，2次路程差为6 m，波速取3×108m/s，可以得出2次脉冲响应的时间间隔为s/v=20 ns。从图3中还可观察到负载在此电流元的激励下的瞬态干扰电压最大在7 mV左右。每次响应都先是一次较强的反向脉冲，然后是正向的数次衰减脉冲。这主要有2方面的原因：（1）因为双指数函数脉冲在t=0时刻导数不连续，而在公式推导中与引入的jω项相乘，相当于在频域对波形进行二次求导，从而在响应波形开始处引入了冲击函数，相比之下，采用高斯脉冲则不会有这种现象产生。（2）由于传输线与负载端不匹配，干扰信号在负载处发生多重反射，才会有清晰的衰减脉冲显示。

3.2 高斯脉冲干扰信号

高斯脉冲信号具有上升沿平滑，高频分量小，频谱范围窄的特点。运用高斯脉冲作为源可以清楚地看清信号较低频率范围内对平行双线的干扰情况。高斯脉冲干扰源的数学表达式为：

i(t)dl=ae-(t-b)2/c2φ(t)

这里取值a=1000，b=25，c=10。

根据信号与系统原理，只有信号发生变化，而系统不变，即系统的传输函数不变，则求解系统响应时只需替换干扰源的频谱函数。在频域与系统的传输函数相乘，得到即为系统响应的频域波形，做傅里叶反变换即可得时域波形，如图4。

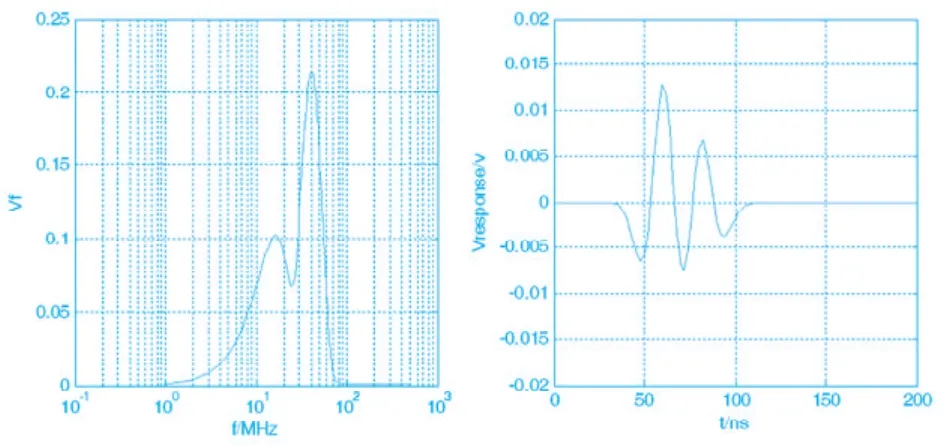
图4 高斯脉冲干扰下的系统时频响应

从图3和图4中可以对比的看出干扰信号的能量都主要集中在10 MHz到100 MHz之间。对于双指数脉冲而言，因其时域波形上升沿较陡，信号含高频成分丰富，因而在系统响应中可清楚地看到，在高于100 MHz以上部分直到1GHz都有明显地干扰；而高斯脉冲上升沿相对平滑，其高频部分能量几乎为零，因而对系统的影响在高于100 MHz频率范围也极小。

从时域的角度来看，双指数脉冲信号产生的干扰信号影响时间短，而高斯脉冲引起的干扰较长，这是由于双指数脉冲引起的干扰频率范围广，从而时域信号窄，高斯脉冲的干扰频谱范围较窄，因而系统响应干扰信号在时域展宽，影响时间变长。这里为什么看不到明显的2次干扰波形，也主要是因为每次脉冲波形时间较长，前后2次脉冲混合叠加在一起作用的结果。

4 结束语

通过扩展的BLT方程来计算强电磁脉冲对平行双线传输线的耦合情况，核心思想是用传输线理论来进行近似计算，采用矩阵方程的方式便于运用计算机进行高速运算，分别计算了2种不同骚扰源作用情况下，平行双线传输线终端负载处的响应波形。在本文模型和条件下，干扰信号频谱主要集中在10 MHz到100 MHz之间，响应幅度在0.01 V到0.02 V作用，主要会发生2次响应，响应间隔的时间为20 ns。从本文的计算与仿真验证的结果看，在一定的频率范围和适当的假设前提下，采用扩展BLT方程计算结果是比较理想的。

实际应用到列车信号线上受干扰情况，要测量或查阅到瞬态电磁场的特性，引入实际电缆的相关参数，必要时进行适当的简化和代替，最后通过运算可以预测作用在信号线上干扰电压的量级和频率范围等。这种方法相对于其它方法更加简洁高效，矩阵运算可以采用现代计算机进行高速运算，而且算法具有可移植性。当然，电磁拓扑法的广泛应用还需要大量实践和经验来完善和扩充。

[1]Liu TK, Tesche F M. On the analysis of general multiconductor transmission line networks[J]. Interaction Note, 1978, 350:1-26.

[2]Baum C E. On the addition of EM field propagation and coupling effects in the BLT equation [J]. Interaction Note, 2003,588:1-43．

[3]安 霆，刘尚合. 基于BLT方程的电磁干扰建模[J]. 高压电技术，33（12）：55-58.

[4]Ianoz M.V，Karisson T. EMC analysis methods and computational models[M]. New York, John Wikey and sons, 1997.