无砟轨道连续梁桥与道岔纵向相互作用规律的研究
2011-05-04徐桂弘
徐桂弘,徐 浩,王 平,代 丰
(西南交通大学 高速铁路线路工程教育部重点实验室,成都 610031)
为适应列车高速行车需要、提高线路稳定性和耐久性、减少线路维修工作量[1],高速轨道对路基和道床提出了很高的要求,为保证轨道的强稳定性和高平顺性,采用板式无砟轨道的结构形式已成为一种趋势[2]。在桥上铺设无缝道岔时其轨下基础主要有三种类型:“门”形筋混凝土道床、带限凸台的道床板、底座纵连式道岔板。本文主要研究前两种无砟轨道结构形式的岔桥纵向相互作用规律。
1 无砟轨道线桥墩一体化计算模型
无砟轨道线桥墩一体化计算模型平面图如图1所示。

图1 桥上无缝道岔模型平面图
桥上无砟轨道上铺设无缝道岔时,道岔铺设在钢筋混凝土道岔板上,若道岔板和桥梁之间铺设中间垫层,则允许二者之间有相对滑动,通过设置纵横向凸台传递作用力,此时道岔和桥梁之间的相互作用与有砟轨道是不相同的,可把桥上无缝道岔结构看作一个由道岔、轨道板、梁体组成的三层结构体系,道岔和轨道板之间的扣件采用弹簧模拟,轨道板和梁体通过弹簧连接,如图2所示。若道岔板和桥梁之间采用“门形筋”联结,则不允许二者之间有相对滑动,此时可把桥上无缝道岔结构看作一个由道岔、梁体组成的两层结构体系,如图3所示。
利用ANSYS软件开放的体系结构,基于 ANSYS二次开发技术,编制了梁轨相互作用非线性有限元程序,自动完成有限元建模、荷载的施加和方程的求解。
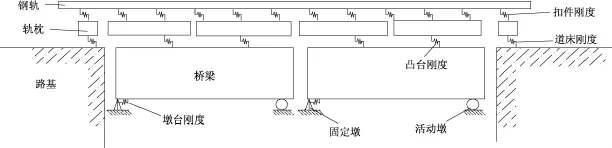
图2 带纵向凸台无砟轨道桥上无缝道岔模型立面图
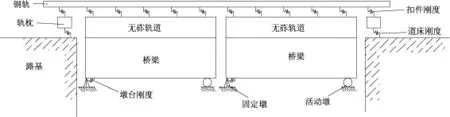
图3 带“门”形筋无砟轨道桥上无缝道岔模型立面图
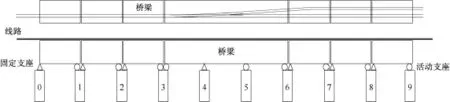
图4 道岔—桥梁布置
2 无砟轨道桥上无缝道岔纵向相互作用
2.1 计算参数
以一组60 kg/m钢轨客运专线18号可动心轨道岔布置在(32+48+32)m连续梁上为例,梁岔布置情况如图4所示。无砟轨道考虑“门”形筋及限位凸台两种形式,凸台支座纵向刚度取为250 kN/mm,道岔区内设置三块道床板,长度分别为20 m,29 m,20 m,道床板温度变化为24℃。
该无缝道岔全长69 m,位于连续梁正中,道岔头尾距离连续梁两端均为21.5 m。连续梁固定支座位于道岔前端;道岔两边各布置3跨32 m简支梁。
线路纵向阻力按每枕12 kN计算,岔区每枕纵向阻力按枕长分布为4.6 kN/m,轨枕间距为0.6 m。扣件阻力取为Ⅱ型扣件常阻力值12.5 kN/组。道岔采用双限位器,其阻力取为分段线性阻力,当限位器子母块贴靠,两轨相对位移<1 mm时,限位器阻力取为1.5×105kN/m;当两轨相对位移>1 mm时,限位器阻力取为6×104kN/m,限位器子母块间隙取为7 mm。道岔长翼轨间隔铁阻力采用线性阻力,取为5×104kN/m。
无砟轨道桥梁日温差取为20℃。两边桥台的墩台纵向刚度为1×107kN/m,中间简支梁桥墩的刚度均为1×105kN/m,而连续梁桥墩的刚度为1×106kN/m。各梁跨均为双线整体箱梁,截面形心距上翼缘为1.626 6 m,距下翼缘为1.577 4 m,截面惯性矩为3.704 4 m4/线。
2.2 计算结果
两种类型(“门”形筋混凝土道床、带限位凸台的道床板)无砟轨道桥上无缝道岔基本轨温度附加力、基本轨伸缩位移,与有砟轨道桥上无缝道岔、普通无砟轨道桥上无缝线路、无砟轨道路基上无缝道岔的钢轨温度附加力、伸缩位移比较,如图5、图6所示。
从图5中可见,两种类型无砟轨道的最大温度附加力均大于有砟轨道无缝道岔;带有限位凸台的无砟轨道温度附加力小于“门”形筋无砟轨道,这主要是由于道床板与桥梁间通过凸台支座纵向弹簧相连,减缓了桥梁传递至道岔上的纵向力;普通桥上无缝线路最大温度附加力出现在连续梁右端,幅值要小于桥上无缝道岔;路基上无缝道岔最大温度附加力出现在尖轨跟端,幅值也要小于铺设于桥梁上的无缝道岔。
从图6中可见,两种类型无砟轨道的钢轨位移均大于有砟轨道桥上无缝道岔,普通桥上无缝线路在连续梁右端具有最大值,路基上无缝道岔伸缩位移远小于桥上无缝道岔。

图5 基本轨温度附加力
两种类型无砟轨道桥上无缝道岔与有砟轨道桥上无缝道岔、普通无砟轨道桥上无缝线路、无砟轨道路基上无缝道岔五种工况下的计算结果对比如表1所示。表1中的钢轨位移及墩台纵向力以向右为正。
从表1中可见,与有砟轨道桥上无缝道岔相比,“门”形筋及带限位凸台无砟轨道桥上无缝道岔因道床阻力大,尖轨及心轨相对道岔板的伸缩位移要小一些,但基本轨温度附加力及连续梁桥墩、岔前简支梁墩台受力有所增大;采用限位凸台无砟轨道结构,基本轨及桥梁墩台受力均小于“门”形钢筋无砟轨道。
3 限位凸台纵向刚度的影响
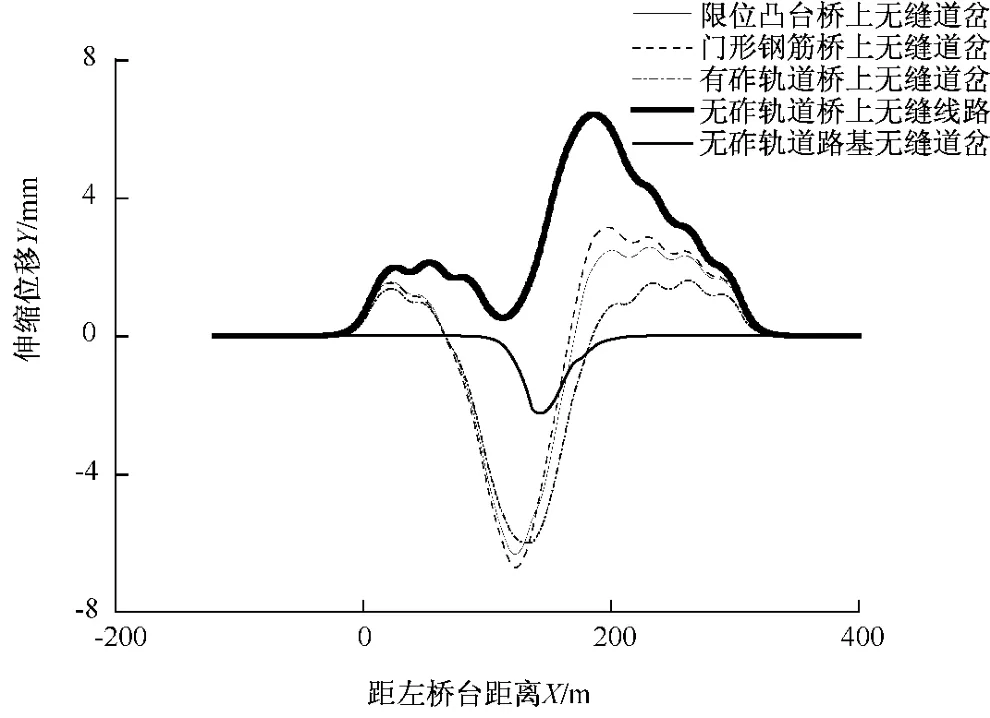
图6 基本轨伸缩位移
岔桥布置如图4所示,道岔板分为三块,转辙器、导曲线及辙叉部分各为一块道岔板,道岔板中间设置纵横向凸台,单个凸台支座刚度设为 150,200,250,300,350 kN/mm,其它计算参数同前。
不同凸台支座刚度情况下的计算结果如表2所示。表2中的钢轨位移、墩台及道岔板纵向力以向右为正。从表2中可见,随着凸台支座刚度的增大,基本轨温度附加力、连续梁桥墩、各道岔板及翼轨末端间隔铁受力均随之增大,尖轨尖端相对道岔板的相对位移、凸台支座胶垫压缩量则呈降低趋势,当单个凸台的支座刚度>250 kN/mm时,凸台支座胶垫的压缩量,即道岔板在凸台支座处与桥梁的相对位移均<1 mm。
4 道岔板分块的影响
岔桥布置如图4所示,道岔分块考虑以下四种方案:工况一:道岔板1块,每块道岔板中间设置5个横向凸台,每块板长约69 m;工况二:道岔板3块,每块道岔板中间设置3个横向凸台,每块板长约23 m;工况三:道岔板5块,每块道岔板中间设置2个横向凸台,每块板长约14 m;工况四:道岔板7块,每块道岔板中间设置1个横向凸台,每块板长约7 m。
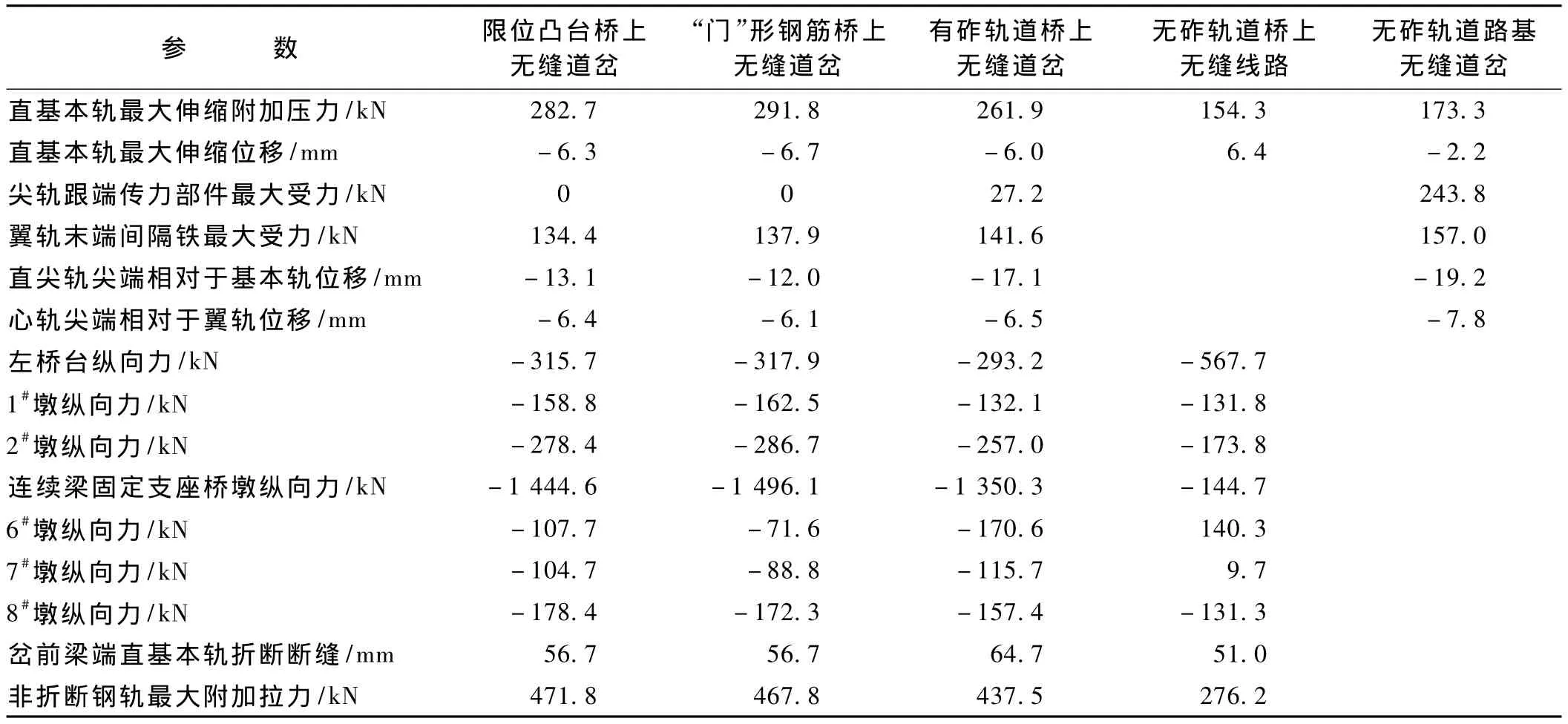
表1 计算结果比较
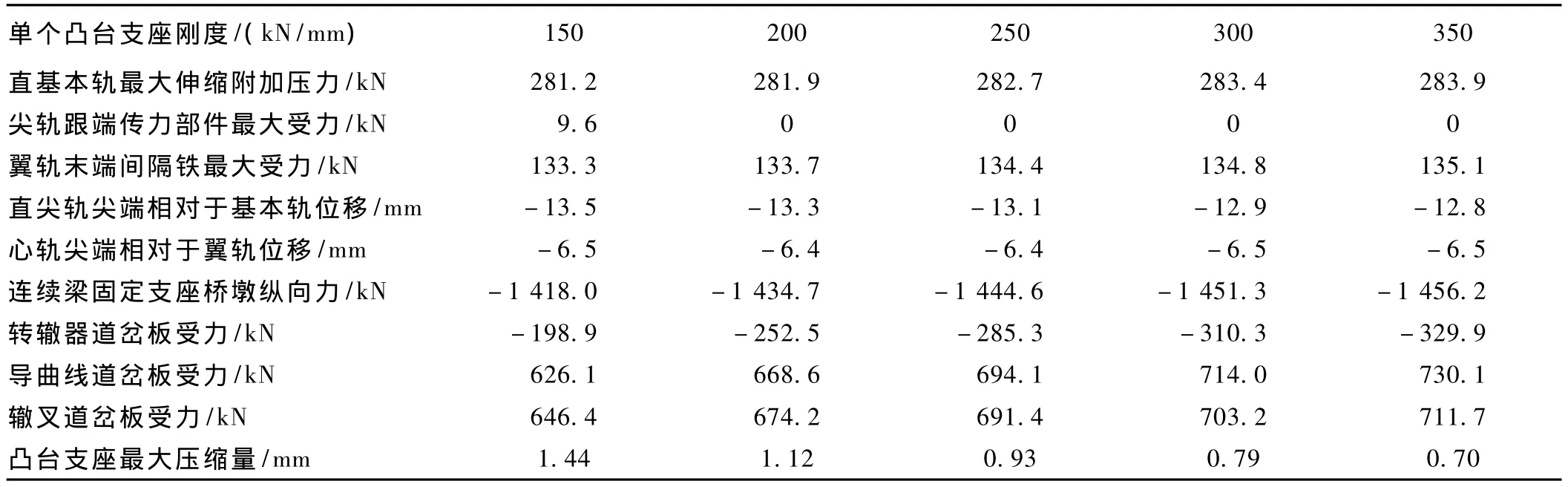
表2 计算结果比较
单个凸台的支座刚度为250 kN/mm,结果如表3,表中钢轨位移、墩台及道岔板纵向力以向右为正。
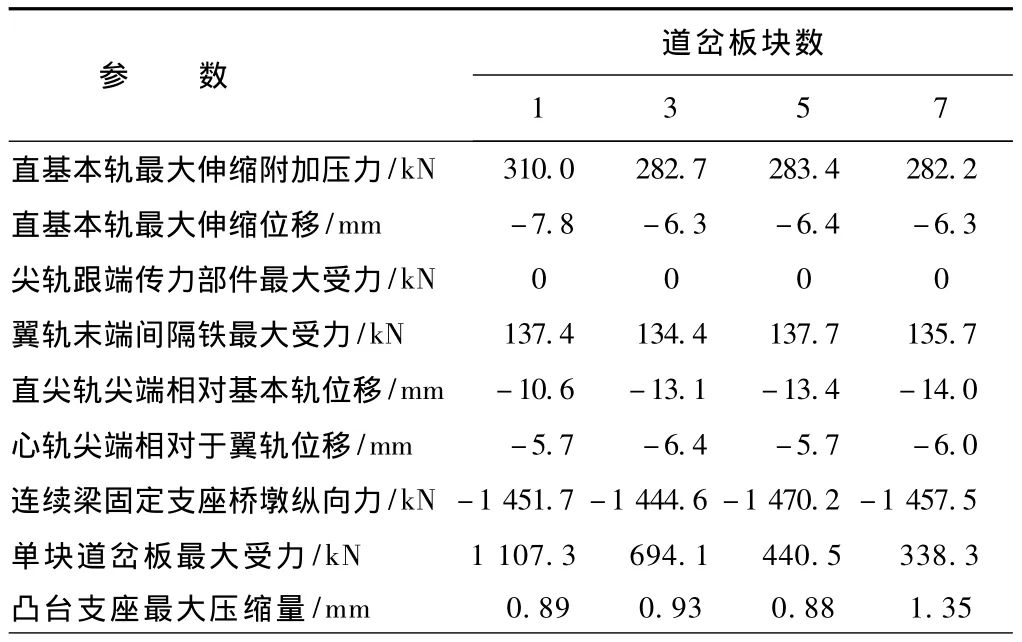
表3 计算结果比较
从表3中可见,道岔板分块数越多,基本轨温度附加力、伸缩位移、单块板的受力均呈降低趋势,但尖轨及心轨尖端相对道岔板的伸缩位移则呈增加趋势;当采用7块道岔板时,需在每块板下设置2个横向凸台才可使支座胶垫压缩量控制在1mm以内,横向凸台的数量要多于其它分块形式;当采用1块道岔板时,虽然尖轨及心轨相对道岔板的伸缩位移最小,但基本轨温度附加力及单块道岔板受力较大,且施工难度较大;18号无砟道岔采用3块道岔板是较为合适的。
5 道岔板温度变化的影响
岔桥布置如图4所示。由于无砟轨道道岔板位于桥面上,且由于高速铁路箱型梁的“温室效应”,道岔板的升降温幅度均较桥梁大,无砟轨道桥梁日温差取为20℃,设道岔板的日温差取为20℃,24℃,30℃,35℃,其它计算参数同前。道岔板不同温度变化幅度的计算结果比较如表4所示。
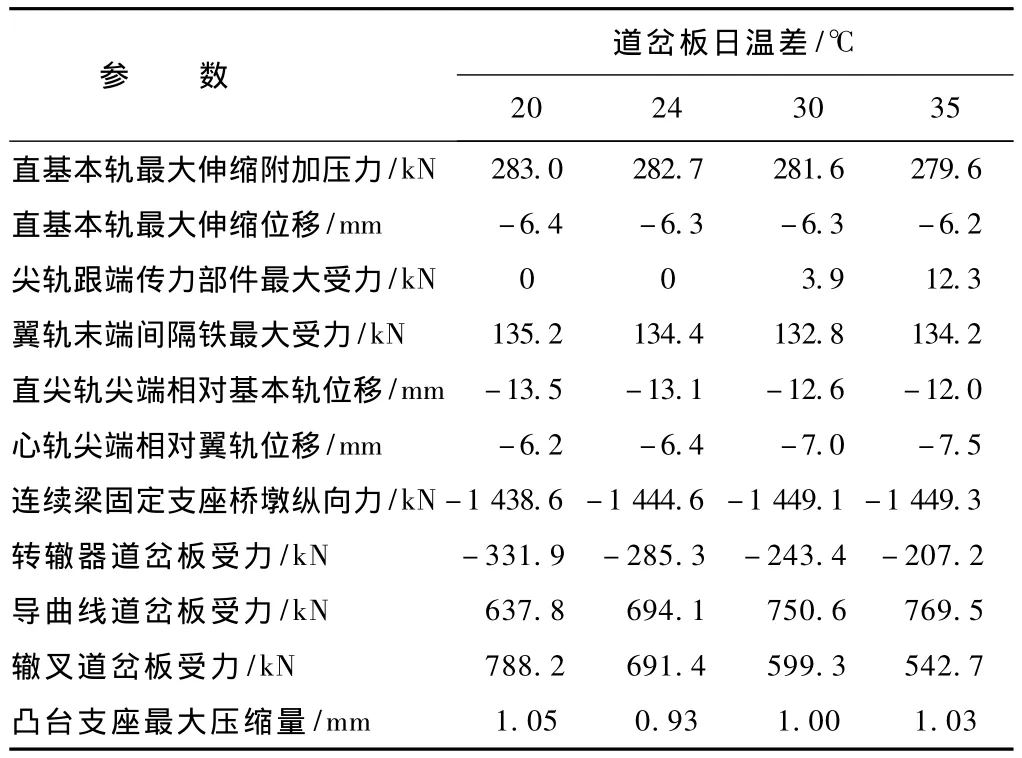
表4 计算结果比较
从表4可见,随着道岔板日温差增大,基本轨温度附加力、伸缩位移、翼轨末端间隔铁受力、直尖轨尖端相对道岔位移、转辙器道岔板受力、辙叉道岔板受力均随之减小,而心轨尖端相对道岔板位移、导曲线道岔板受力、连续梁固定墩受力则随之增大,这主要是由于道岔板沿凸台的伸缩导致道岔与桥梁的相对位移改变所致。
6 结论
本文主要分析了“门”形筋混凝土道床、带限位凸台的道床板的岔桥纵向相互作用规律。分析结果表明:
1)随着桥梁日温差增大,两种类型无砟轨道的最大温度附加力均大于有砟轨道无缝道岔;带有限位凸台的无砟轨道温度附加力小于“门”形筋无砟轨道;路基上无缝道岔最大温度附加力出现在尖轨跟端。
2)带有限位凸台的无砟轨道钢轨位移小于“门”形筋无砟轨道;两种类型无砟轨道的钢轨位移均大于有砟轨道桥上无缝道岔,普通桥上无缝线路在连续梁右端具有最大值,路基上无缝道岔伸缩位移远小于桥上无缝道岔。
3)“门”形筋及带限位凸台无砟轨道桥上无缝道岔因道床阻力大,尖轨及心轨相对道岔板的伸缩位移较小,但基本轨温度附加力及连续梁桥墩、岔前简支梁墩台受力有所增大。
4)随着凸台支座刚度的增大,基本轨温度附加力、连续梁桥墩、各道岔板及翼轨末端间隔铁受力均随之增大,尖轨尖端相对道岔板的相对位移、凸台支座胶垫压缩量则呈降低趋势。
5)随着道岔板分块数增多,基本轨温度附加力、伸缩位移、单块板的受力均呈降低趋势,但尖轨及心轨尖端相对道岔板的伸缩位移则呈增加趋势。
6)随着道岔板日温差增大,基本轨温度附加力、伸缩位移、翼轨末端间隔铁受力、直尖轨尖端相对道岔位移、转辙器道岔板受力、辙叉道岔板受力均随之减小,而心轨尖端相对道岔板位移、导曲线道岔板受力、连续梁固定墩受力则随之增大。
[1]何华武.无砟轨道技术[M].北京:中国铁道出版社,2005.
[2]赵东田,王铁成,刘学毅,等.板式无砟轨道 CA砂浆的配制和性能[J].天津大学学报,2008(7):793-799.
[3]徐振龙,钱振地,秦德进.不同结构形式无砟轨道施工对比分析[J].铁道建筑,2005(3):59-64.
[4]贺挨宽.无砟轨道施工平面控制主要技术标准的研究[J].铁道工程学报,2006(9):27-30.
[5]徐振龙,王智勇.板式无砟轨道综合施工技术研究[J].铁道建筑,2005(2):35-40.
[6]曾志,郑新国,翁智财,等.CRTSⅡ型板式无砟轨道水泥乳化沥青砂浆施工技术[J].铁道建筑,2009(9):97-100.
[7]林晓波.无砟轨道用弹性混凝土的试验与研究[J].铁道建筑,2007(11):79-80.
