SPH方法在自由表面流体研究中的应用
2011-05-03缪吉伦陈景秋张永祥
缪吉伦,陈景秋,张永祥
(1.重庆交通大学西南水运工程研究所,重庆 400016;2.重庆大学资源环境学院,重庆 400030)
近年来,在流体力学计算领域发展起来一种新型的数值计算方法,即光滑粒子流体动力学法(SPH方法)。SPH方法是一种无网格的纯Lagrange方法,1977年由Gingold等[1]提出,最初主要用于解决天体物理学中流体质团无边界情况下的三维空间任意流动的计算问题。SPH方法无需网格,避免了网格生成的麻烦,而且解决了通常拉氏方法中的网格缠结和扭曲以及网格重划的问题。近年来,国内外学者采用SPH方法在固壁边界和自由表面流动等方面进行数值模拟计算,取得了一定的研究成果。
1 SPH方法的基本原理
与传统的基于网格的方法(如FDM法和FEM法)相比,SPH方法的主要优点在于不需要使用任何提前定义的提供结点连接信息的网格,它用一系列任意分布的粒子质点来代表整个连续介质流体并估计相应的偏微分方程。
SPH方法基于以密度、速度、能量等为变量的偏微分方程组,将描述场的函数用核函数逼近近似表达为任意函数和核函数的乘积的积分:

式中:x与x′为计算域内任意2点的坐标;<f(x)>表示坐标 x处的核估计值;D为整个求解区域;f(x′)为坐标 x′处的场量值;h为光滑长度;W(xx′,h)为核函数,它有 2个自变量:粒子间距离和光滑长度h。
2 流体SPH数值方法
2.1 Navier-Stokes方程的SPH粒子近似式
参照SPH方法的粒子近似过程,可以将Navier-Stokes方程写成以下粒子近似方程[2](不考虑黏度):
质量守恒方程

动量守恒方程

式中:ρi,ρj分别为粒子i和粒子j的密度;t为时间;N为粒子i的支持域中粒子的总数;v为粒子速度;mj为粒子j的质量;Wij为粒子j对粒子i产生影响的光滑函数;α,β表示坐标方向;p为压力;μ为动力黏性系数;ε为剪切应变率;e为单位质量物质的内能。
根据人工压缩性,可把一般的不可压缩流体看作可压缩流体。通过在水的状态方程引入压缩率可模拟具有自由表面的流动:

式中:ρ0是粒子的初始密度;γ为系数,对于水取γ=7;B为用于限制密度的最大改变量,一般为初始压力。
2.2 光滑核函数的选取
核函数除满足归一性和δ函数条件外,还必须具有良好的紧支性,目前常用的核函数有高斯核函数、三次样条函数、五次样条函数等。应用较广的B样条光滑函数如下[2]:

式中:αd为归一化常数,在一维、二维、三维情况下分别是1/h,15/(7πh2),3/(2πh3)。
2.3 边界处理方法
将入口边界、出口边界看成特殊自由边界,界面处的粒子压力赋值为零或一定的外压力值。将固壁边界离散成为边界粒子,并假定边界粒子对靠近它的流体粒子施加一个大小适当的中心排斥力,以阻止流体粒子穿越固壁边界,且排斥力只在近距离上起作用。文献[3]将边界力描述为式中:A,n,s为可调参数;r0为粒子初始间距;r为当前时刻边界粒子和流体粒子的间距;r为长度矢量。当 r>r0时置 f(r)=0。
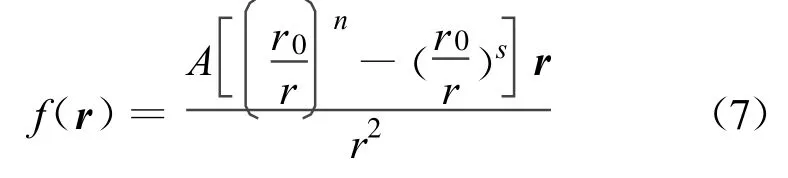
2.4 数值求解
对转换后的常微分方程组进行时间积分,一般采用显式格式,如预测校正方法、四阶 Runge-Kutta方法、标准蛙跳法等,还可用中心差分、Lax-Wendroff差分格式等。对于不可压缩流体自由表面流动情况,为避免显式计算产生振荡,有学者提出用分数步长法分2步求解。为保证解的收敛性,时间步长Δt应满足CFL条件。
3 SPH方法在自由表面流研究中的应用
SPH方法作为一种无网格方法,在处理移动边界问题尤其是大规模扭曲和自由表面问题时具有明显优势。从目前国内外研究成果来看,SPH方法在流体领域主要应用于以下几个方面。
3.1 溃坝问题
溃坝问题是国内外研究者比较关注的一个课题,目前的研究多采用FVM,FEM,VOF等方法,而SPH方法由于能逼真复演流体飞溅、融合等复杂自由表面现象而被日益关注。
解决溃坝模拟问题时主要用到Cross液流模型,它能使有效黏性力成为连续变量且避免了数值不稳定性问题,可广泛应用于牛顿流体及非牛顿流体中。Shao等[4]运用预测校正法(分数步长法)求解了不可压缩流体的SPH方程组,按时间步长不断迭代逐步得到不同时刻的粒子位置及流速、压力等物理量,并模拟出流体碰壁以后的飞溅和融合等现象。经比较,数值模拟结果与解析解非常相近,且随着粒子数的增加收敛速度加快。Colagrossi等[5]也用SPH方法模拟了溃坝过程,着重分析了波浪前端撞击壁面后回落到表面的过程。当浪端回落至与上层表面构成封闭环状空间时,内部气体被压缩,使得压力已不同于大气压力,两相密度的突变是算法不稳定的主要来源,他们将SPH方程中的mj/ρi代之以mj/ρj,避开了这一问题。用修正后的公式成功模拟出流体碰壁回落的过程,与固定网格上解得的Navier-Stokes方程结果一致。
3.2 河冰、海冰模拟方面
目前,大多数海冰与湖冰的动力学模拟采用有限差分法,存在严重的数值扩散问题且冰体内部温度场准确性不理想。尤其当大型冰体边缘移动时,网格单元会迅速扭曲[6]。随着纯Lagrange粒子方法的产生,这些问题可以迎刃而解。Shen[7]首次将SPH方法应用于河冰模拟,采用SPH耦合FEM方法建立二维数值模型,模拟出复杂的几何和流动条件下河冰的表面阻塞及动态运输过程,通过两相界面处的相互作用将冰动力学及水力学分量结合起来,在水力学方程中考虑了冰层中水的排出量,用非线性渗流理论模拟冰层中的出流,使水的质量守恒,对冰的模拟更加准确。用此模型研究了在密苏里河下游使用拦冰栅以减少密西西比河河冰输出的可行性。Oger[8]采用SPH方法模拟了风力作用下浮冰在水面上的运动状态,并通过引入黏塑性模型考虑了浮冰的流变,数值分析结果与解析解相符。
Ricardo[9]应用SPH方法对海冰进行数值模拟,并利用黏塑性海冰液流模型求解冰场运动方程,从而模拟出断裂海冰流在楔形渠道内的运动。王刚等[10]引入SPH方法对辽东湾的区域性漂移海冰进行了数值模拟,在采用黏塑性海冰本构方程的基础上考虑了热力学因素对其厚度、密集度的影响,得到热力动力模式的控制方程,研究了海冰厚度和速度矢量的分布规律,模拟出符合实际的海冰演化过程。
3.3 大坝溢流
孙凯[11]对Omkareshwar溢流坝的坝面水流特性进行了研究。李大鸣等[12]将SPH数学模型引入拉西瓦水电站表孔泄流中,提出采用补水边界的方法来满足库区恒定水位条件,模拟了表孔溢流的流场变化及粒子运动过程。计算结果表明光滑粒子可用于模拟高速水流中非线性大变形流动问题。
3.4 流固耦合问题
SPH方法在求解流固耦合问题方面得到了初步应用。Edmond等[13]采用SPH和LES耦合方法对近海岸单波运动机理进行了初步研究,结果显示,数值模拟的单波剖面与试验数据以及解析解结果几乎完全一致;他们还采用SPH结合大涡模型模拟近岸孤立波的爬升,分析了规则及不规则波浪冲越近海构筑物的运动过程,研究成果与相应试验中的观测结果非常相近。Mutsuda等[14]将SPH方法应用于沿海岸波浪与结构物相互作用的研究中,数值模拟了波浪与刚性、弹性建筑物相互作用中建筑物产生的运动、变形情况,试验结果证实了SPH方法的有效性和精确性。Gómez-Gesteira等[15]对波浪冲越坝体时的形状和幅度进行SPH数值模拟,并对冲击的位置、速度、压力进行了比较分析,结果与试验数据吻合很好。Gotoh等[16]研究了波浪与半淹没的防波堤的相互作用。
块体滑坡往往引起自由水面的剧烈变化。Monaghan等[17]研究了矩形块体沿弧形坡面下滑撞击入水的过程,介绍了刚体与水相互冲击的室内试验和数值模拟结果。2006年,Oger[8]在SPH框架中引入了粒子搜索方法及一种可估计流体对固体边界作用力大小的方法,用于获得流固耦合问题中自由运动物体的动力响应,并以不同楔形体滑入水体的试验结果证实了这种方法的适用性,并指出需要更多的试验来证实这种方法的可行性,此外还应在求解过程中考虑空气的运动状态。
3.5 水下爆破
Liu等[2]应用SPH方法模拟了水下爆破现象。通过对板条和球形TNT炸药的数值模拟算例,应用SPH方法研究了高能炸药的真实爆炸模型和人工爆炸模型,同时也对冲击效应的水介质缓冲进行研究。为了适应水下爆炸冲击模拟的需要,提出了处理物质交界面的算法,即在那些彼此之间将要发生穿透的粒子上施加惩罚力,并且允许在不同材料和介质的粒子间进行核近似和粒子近似。因此,这种交界面处理方法不仅能通过核近似和粒子近似施加交界面边界条件,而且能够有效地防止不同介质粒子之间的非物理穿透。
3.6 多相流的研究
在多相流的研究方面,Monaghan等[18-19]研究了火山喷发中气尘两相运动;Cleary[20]研究了多物质热传导问题;Richie等[21]研究了多物质星云的形成过程;Colagrossi等[22]、韩旭等[23]在理想气体状态方程中引入van der Waals修正项并对粒子运动速度进行修正,研究了密度差异较大时两相流的流动问题等。近年来,国外有学者开始应用SPH方法研究泥石流、火山流动等问题。
3.7 船舶流体力学
SPH方法用于船舶流体力学仅见于近期的研究。Gómez-Gesteira[24]利用SPH方法对甲板上浪问题进行研究,得到了甲板上浪的水面形态、甲板上流体的流速变化以及甲板的受力状况;Landrini等[25]用BEM方法结合SPH方法计算船体阻力,船体表面的速度分布采用BEM方法计算,船艏与船艉波的破碎演化过程则采用SPH方法模拟。Benedict等[26]用SPH方法模拟求解有限水深的水翼绕流问题。Souto等[27]模拟了减摇水舱运动与液体所产生的力矩之间的相位滞后问题,对液舱晃荡所产生的力矩幅值进行了计算,结果表明该方法能够达到较高的精度。通过这些研究可以看出SPH方法对自由表面波的翻卷、破碎、重入等细节的模拟可以达到较高的精度。在模拟液舱晃荡问题时,SPH方法计算局部冲击压力具有较高的精度,但整体力矩的计算精度不如传统网格方法的计算精度高。国内还没有SPH方法用于船舶水动力学的论文报道。
3.8 其他领域
在其他领域方面,Mǘller等[28]通过在 Navier-Stokes方程中引入表面张力项,应用SPH方法模拟了人体组织中的血液流动。Valizadeh等[29]在研究两相流问题时,对界面粒子质量进行修正,成功模拟了气泡在流体中的上升及溃灭过程,并复演了2种流体密度差异较大时的潜入现象。Roubtsova等[30]利用SPH方法结合某一地区的三维地形处理洪水演进的范围,以此确定危险区域。此外,SPH方法也应用于电影特效和游戏中的波浪流动、海啸对海岸线的冲击等方面。
4 SPH方法的局限及发展方向
由于SPH方法无需生成网格,避免了大量的单元划分,克服了有限元方法局部近似所引起的误差,能够适应扭曲变形,在大变形问题中自适应性强。SPH方法近年来在流体研究领域发展迅速,但也存在以下局限[31-32]:①光滑函数的选择尚无明确标准。光滑函数决定了近似模式和粒子的有效支持域,特别是中心峰值对SPH方法的近似精度起着重要的作用。目前已经提出了多个光滑核函数形式,但针对某具体问题应选择哪种核函数并无明确标准。②边界粒子的处理方法存在缺陷。边界上或临近边界的粒子在积分时会被边界截断,故SPH方法不能完全适用于整个区域。虽然目前采用了虚粒子法改进,边界粒子结果仍不理想。③计算工作量大,影响运行速度。在计算中可能出现张力不稳定性振荡,导致计算不收敛。
针对SPH方法的内在缺陷,一些学者提出了相应的修正或改进方法,SPH方法的稳定性、精度、收敛性也提高很多。然而,目前的分析大多基于均匀分布的粒子,对于如粒子高度分布无序、粒子的光滑长度有变化等更普遍的情况尚有待研究。流场边界附近粒子运动的压力特性,其计算结果的可靠性尚未验证。在边界处理中,如何引入数学表达使边界的精度得到提高,从而避免由于边界不稳定导致扩散还需进一步研究,对SPH方法耗时的临近粒子搜索计算问题需进行进一步的讨论,以满足实时试验的要求。总之,虽然SPH方法在诸多领域得到了应用,但尚未形成完善的理论体系,目前应巩固SPH方法的理论基础,在修正其内在缺陷方面作进一步研究。
[1]GINGOLD R A,MONAGHAN J J.Smoothed particle hydrodynamics:theory and application to non-spherical stars[J].Monthly Notices of the Royal Astronomical Society,1977,181:375-389.
[2]LIU Gui-rong, LIU Mou-bing.Smoothed particle hydrodynamics:a meshfree particle method[M].Singapore:World Scientific Publishing Company,2003:26-32.
[4]SHAO Song-dong,GOTOH H.Pressure analysis of dam-break and wave-breakingby SPH model[J].Annual Journal of Hydraulic Engineering,JSCE,2003,47:403-408.
[5]COLAGROSSI A,LANDRINI M.Numerical simulation of interfacial flows by smoothed particle hydrodynamics[J].Journalof Computational Physics,2003,191(2):448-475.
[6]孙晓艳,王军.SPH方法的理论及应用[J].水利水电技术,2007(3):44-46.
[7]SHEN Hung-tao.SPH simulation of river ice dynamics[J].Journalof Computational Physics,2000,165(2):752-770.
[8]OGER G.Two-dimensional SPH simulation of wedge water entries[J].Journal of Computational Physics,2006,213(2):803-822.
[9]RICARDO G.Flow of fractured ice through wedge shaped channels:smoothed particle hydrodynamics and discrete element simulations[J].Mechanics ofmAterials,1998,29(12):1-17.
[10]王刚,李海,季顺迎.基于光滑质点流体动力学的海冰热力-动力数值模式[J].水科学进展,2007,18(4):523-530.
[11]孙凯.基于SPH方法对自由表面流的数值模拟及可视化研究[D].郑州:郑州大学,2007.
[12]李大鸣,刘江川,徐亚男.SPH法在大坝表孔泄流数值模拟中的应用[J].水科学进展,2008,19(6):841-844.
[13]EDMOND Y M L,SHAO Song-dong.Simulation of near-shore solitary wave mechanics by an incompressible SPH method[J].Applied Ocean Reasearch,2002,24:275-286.
[14]MUTSUDA H,SHINKURA Y.An eulerian scheme with lagrangian particlesforsolving impactpressure caused by wave breaking[C]//Proceedings of the Eighteenth International Offshore and Polar Engineering Conference.Vancovver:ISOPE,2008:162-165.
[15]GÓMEZ-GESTEIRA M,DALRYMPLE R A.Using a 3D SPH method for wave impact on a tall structure[J].Journal of Waterway Port Coastal and Ocean Engineering,ASCE,2004,130(2):63-79.
[16]GOTOH H,SHAO Song-dong.SPH-LES modelfor numerical investigation of wave interaction with partially immersed breakwater[J].Coast Eng J,2004,46(1):39-63.
[17]MONAGHAN J J,KOS A,ISSA N.Fluid motion generated by impact[J].Journal of Waterway Port Coastal and Ocean Engineering,ASCE,2003,129(6):250-259.
[18]MONAGHAN J J,KOCHARYAN A.SPH simulation ofmultiphase flow[J].Computer Physics Commun,1995,87(1/2):225-235.
[19]MONAGHAN J J.Implicit SPH drag and dusty gas dynamics[J].Journal of Computational Physics,1997,138(2):801-820.
[20]CLEARY P W.Modelling confined multimaterial heat andmAss flows using SPH[J].AppliedmAthematical Modelling,1998,22:981-993.
[21]RICHIE B W,THOMAS P A.Multiphase smoothed particle hydrodynamics[J].Mon Not R Astron Soc,2001,323(3):743-756.
[22]COLAGROSSI A,LANDRINI M.Numerical simulation of interfacial flows by smoothed particle hydrodynamics[J].Journalof Computational Physics,2003,191(2):448-475.
[23]韩旭,杨刚,龙述尧.SPH方法在两相流动问题中的典型应用[J].湖南大学学报:自然科学版,2007,34(1):28-32.
[24]GÓMEZ-GESTEIRA M.Green water overtopping analyzed with a SPH model[J].Ocean Engineering,2005,32:223-238.
[25]LANDRINIM,COLAGROSSI A,TULIN M P.Breaking bow and stern waves:numerical simulations[EB/OL].[2001-04-22].http://www.iwwwfb.org/Abstracts/iwwwfb16/iwwwfb16-23.pdf.
[26]BENEDICT D R,DALRYMPLE R A,GESTEIRA M,et al.SPH for naval hydro-dynamics[EB/OL].[2003-04-06].http://www.iwwwfb.org/Abstracts/iwwwfb18/iwwwfb18-43.pdf.
[27]SOUTO A,DELORME L,PÉREZ-ROJAS L,et al.Liquid moment amplitude assessment in sloshing type problems with smooth particle hydrodynamics[J].Ocean Engineering,2006,33:1462-1484.
[28]MÜLLER M,SCHIRM S,TESCHNER M.Interactive blood simulation for virtual surgery based on smoothed particle hydrodynamics[J].Technology and Health Care,2004(12):25-31.
[29]VALIZADEH A,SHAFIEEFAR M,MONAGHAN J.Modeling two-phase flows using SPH method[J].Journal of Applied Sciences,2008,8(21):3817-3826.
[30]ROUBTSOVA V,KAHAVITA R.The SPH technique applied to free surface flows[J].Computers&Fluids,2006,35(10):1359-1371.
[31]SWEDE J W,HICKS D L,ATTAWAY S W.Smoothed particle hydrodynamics stability analysis[J].Journal of Computational Physics,1995,116(1):123-134.
[32]郑兴,段文洋.光滑质点流体动力学(SPH)及其算法特性[J].船舶力学,2008(8):550-559.
