粒子群优化算法在确定越流含水层参数中的应用
2011-05-03张鹄志郭建青
张鹄志,郭建青
(长安大学环境科学与工程学院,陕西 西安 710054)
粒子群优化(particle swarm optimization,PSO)算法[1-2]是由Eberhart R C和Kennedy J于1995年提出的一种基于迭代的智能随机优化算法,具有易于理解和实现、全局搜索能力强[3]和计算结果精度不易受人为因素影响等优点。由于PSO算法具有这些优点,其在水利工程规划设计领域中已经得到了一定的应用。例如,国内学者将PSO算法应用于水库(群)优化调度中,为求解水库调度问题提供了一种新的有效解决途径[4-5];还有的学者将PSO算法引入大坝安全监控领域,并结合多元回归统计模型建立基于粒子群算法的混凝土坝变形预报模型,并通过优化迭代计算确定坝体变形统计模型中各回归系数[6]。在开发利用地下水资源过程中,利用不同的方法分析抽水试验数据,是确定含水层参数的主要途径之一。标准曲线配线法是分析抽水试验数据的常用方法之一,但是,其在应用过程中存在着人为随意性,对计算结果的精度影响较大。为了弥补这个缺陷,人们已将智能优化算法应用于分析抽水试验数据,确定满足泰斯假设条件下的含水层参数[7]。但是,在利用PSO算法分析越流系统含水层中的抽水试验数据并确定含水层参数方面,以及PSO算法中的3个控制参数对算法收敛性和计算结果精度的影响方面开展的研究工作较少。鉴于此,笔者将PSO算法应用于确定第1类越流系统的含水层参数,并通过数值试验,初步讨论算法控制参数c1,c2和 ω对算法收敛性的影响。
1 PSO算法
PSO算法假想一群粒子的每个粒子都在搜索空间中以一定速度飞行,并根据本身以及同伴的飞行经验动态调整自身速度,从而形成群体寻优的机制,最终搜索到问题的最优解[1-2]。人们用粒子的位置表示待优化问题的解,将每个粒子位置的优劣程度称为它的适应度,由待优化问题的目标函数值来定量地表征。每个粒子由1个速度矢量决定其飞行方向和速率大小。设在1个d维的目标搜索空间中,由m个粒子组成1个群体,其中,在第 t次迭代时粒子i的位置表示为Xi(t)=(xi1(t),xi2(t),…,xid(t)),相应的飞行速度表示为 V i(t)=(vi1(t),vi2(t),…,vid(t))。开始运算时,首先随机初始化这m个粒子的位置和速度,然后通过迭代寻找最优解。在每次迭代过程中,各粒子通过跟踪2个极值来更新自己的速度和位置:1个是该粒子本身迄今搜索到的最优解,称为个体极值 pbest,表示为P i(t)=(pi1(t),pi2(t),…,pid(t));另1个是整个粒子群迄今找到的最优解,称为全局极值gbest,表示为Pg(t)=(pg1(t),pg2(t),…,pgd(t))。将每个粒子更新个体极值的过程称为历史寻优,将各不同粒子通过相互比较来更新全局极值的过程称为全局寻优。在第t+1次迭代计算时,粒子i根据下列规则来更新自己的速度和位置[3]:

式中:ω为惯性权重系数;c1和c2为学习因子,文献[3]中建议 c1=c2=2.0;rand1和 rand2分别为 2个在[0,1]区间内变化的随机数;下标k表示第k维。
式(1)右边第1项为个体粒子飞行过程中的“惯性”部分,反映了粒子的运动“习惯”,代表粒子有维持自己先前速度的趋势;第2项为“认知”部分,反映了粒子对自身历史经验的记忆,代表粒子有向自身个体极值逼近的趋势;第3项为“社会”部分,反映了粒子间协同合作与知识共享的群体历史经验,代表粒子有向全局极值逼近的趋势[3]。另外,粒子每一维的速度vik都应被一个最大速度所限制。而为粒子位置设定阈值,从而保证各粒子在限定的搜索空间内飞行,也是有待进一步研究的问题。
2 PSO算法在确定第1类越流系统含水层参数中的应用
2.1 基本公式
本文讨论的第1类越流系统的模型与文献[8]中相同,抽水过程中的水头降深公式为
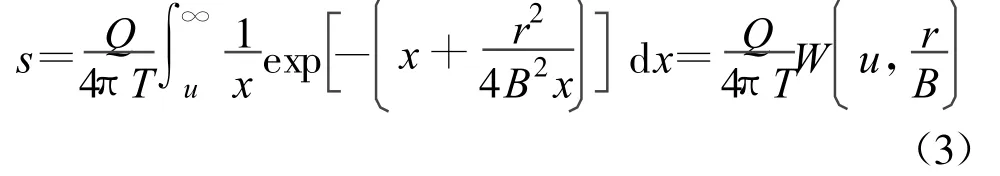
式中:s为水头降深,[L];Q为抽水流量,[L3◦T-1];T为导水系数,[L2◦T-1];r为距抽水主井的距离,[L];1/B为越流补给因子,[L-1]。
在应用PSO算法确定含水层参数时,要求式(4)表达的目标函数值达到最小,即

式中:Xi(t)为第t次迭代时粒子i的位置,它以各含水层参数作为其各维上的坐标,在第1类越流系统中有3个待求的含水层参数,分别是导水系数T、弹性释水系数S和越流补给因子1/B,分别视为xi1(t),xi2(t),xi3(t),这样粒子的位置坐标就是X=(T,S,1/B);j为抽水试验过程中水头降深观测数据的序列号,j=1,2,…,N;soj为实际观测到的第j个降深值,[L];scj为利用式(3)计算的与 soj相同时刻的水头降深值,[L]。
式(4)的意义为选取适当的粒子位置 X=(T,S,1/B),使降深的计算值与其观测值之间的残差平方和的均值达到最小。此时的 T,S,1/B即为所求的最优解。
2.2 算例
根据上述基本公式和PSO算法的流程,利用C语言编写了相应的计算程序,在运行开始时,输入数据为相应不同抽水时间的水头降深值,输出结果为含水层参数T,S,1/B的最优值。
表1中给出了抽水流量Q=17.0m3/min时,距抽水主井距离r=12.19 m的观察孔中观测到的降深随时间的变化数据[10]。

表1 观测数据

根据多次试算的经验,采用的粒子个数为50个;收敛标准取目标函数值小于0.00060842。权重系数按式(4)进行线性衰减:式中:ωmax为最大惯性权重系数,取 0.9;ωmin为最小惯性权重系数,取0.1;t′为当前迭代次数;n为最大迭代次数,取3000。
取学习因子c1=c2=2.0,经过平均700次迭代得到计算结果,见表2。表2也给出了传统配线法的计算结果。
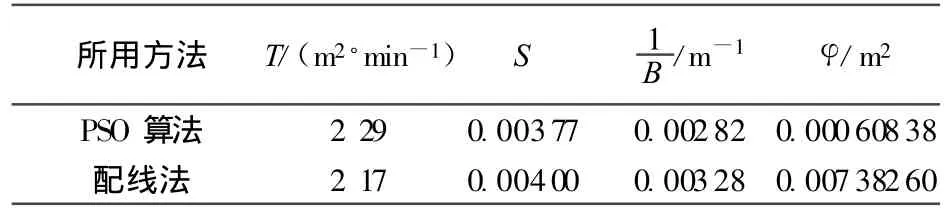
表2 不同方法的计算结果
2.3 可靠性检验及与传统配线法效果比较
分别利用由PSO算法和配线法求出的含水层参数来计算降深~时间曲线,并与实际的降深~时间曲线进行比较,如图1所示。由图1可以看出,PSO算法所求结果对观测数据的拟合程度与传统配线法很接近,是可靠的。但配线法具有较大的主观性,不同人员所得结果的精度可能不同,而PSO算法则可以稳定地得到精度较高的结果。

图1 PSO算法与配线法效果比较
3 PSO算法控制参数的作用和影响
由前文可以看出,有5个参数影响着PSO算法的运算过程和结果,分别是:粒子个数、待求参数初值的取值范围、收敛标准、c1和c2以及 ω。拟通过数值试验结果,分析 c1,c2和 ω对算法收敛性的影响。
3.1 学习因子
3.1.1 定性分析
以 c1为例,从式(1)和式(2)不难看出,c1rand 1[pik(t)-xik(t)]的作用是:在粒子更新位置的过程中,使粒子以“一定程度”向它的个体极值靠拢。而这个“一定程度”是由 c1rand1确定的。比如xik(t)+1.0rand1[pik(t)-xik(t)](即 c1=1.0)就表示粒子向其个体极值随机地移动某一距离;而xik(t)+2.0rand1[pik(t)-xik(t)](即 c1=2.0)表示粒子不但可以飞向个体极值,而且也可以飞过个体极值位置到达另一侧(但不会超出原来相差的距离),如图2所示。因此,当c1=1.0时,粒子直接以其个体极值为目标,靠拢的趋势是最强的;当 c1=2.0时,新位置在个体极值两侧的分布几率是最均衡的。
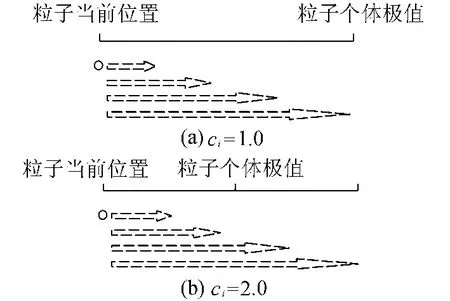
图2 粒子飞行示意图
同理,c2rand2确定了粒子向全局极值移动的程度:当c2=1.0时,粒子向全局极值靠拢的趋势最强;当c2=2.0时,粒子趋于在全局极值周围几率均衡地分布。
3.1.2 数值试验结果分析
文中主要对最具代表性的 ci=1.0和 ci=2.0(i=1,2)情况进行试算。另由于不同目标函数值对应着不同的粒子位置,因此用目标函数值的变化来反映粒子位置的变化情况。
笔者在其他参数取值相同(c2=1.0,ωmax=0.8,ωmin=0.6,粒子个数取 5个,收敛标准取0.00060842)的条件下,含水层参数取值范围为0.93 m2/min≤T≤3.72m2/min,0.002≤S≤0.005,0.0016 m-1≤1/B ≤0.0033 m-1时,对 c1=2.0和c1=1.0分别进行3次试算,输出每个粒子目标函数值随迭代次数增加的变化(篇幅所限未列出具体结果)。通过试算可以观察到2种现象:①c1影响粒子的活跃程度,进而影响粒子的搜索能力:当 c1=2.0时,目标函数值在迭代次数达到2000次以上时仍然有所变化,即粒子仍然移动,保持着搜索能力;当c1=1.0时,目标函数值在迭代次数达到1000次以上时就已经不再变化,即粒子基本失去搜索能力。②当c1=2.0时,3次试算目标函数值分别稳定于0.00061086,0.00061082和0.00061098左右;c1=1.0时,3次试算目标函数值分别稳定于0.00086816,0.00071975和0.00101040,均大于c1=2.0时的结果。显然 c1=2.0时的最终运算结果具有更高的精度。
产生上述现象的原因是,当 c1=1.0时,粒子在每次迭代中都强烈地趋向于它的某个个体极值,因此,在经过较少次的迭代后粒子就会到达某个个体极值附近。这时,负责历史寻优的c2rand1[pik(t)-xik(t)]项就会趋于零(因为这时pik(t)-xik(t)趋于零),从而使历史寻优机制形同虚设,粒子便停滞在这个个体极值而不再随迭代而移动(实际上,试算中c2=1.0的取法加剧了这种作用,它使各粒子的个体极值迅速趋向于某一局部极值)。粒子这种过早的停滞使其不能再搜索到更优的值,因此其最终结果的精度普遍较差。当c1=2.0时,粒子在每次迭代中都能几率均衡地在个体极值两侧进行历史寻优,所以不易停滞,从而保持了更强的历史寻优能力,可以找到更优的值。
对于c2的取值,在其他参数取值相同(c1=1.0,ωmax=0.9,ωmin=0.7,粒子个数取 5 个,收敛标准取0.00060842)的条件下,含水层参数取值范围为:0.93 m2/min≤T≤3.72m2/min,0.002≤S≤0.005,0.0016m-1≤1/B ≤0.0033m-1时 ,对 c2=2.0和c2=1.0分别进行3次运算,其观察到的现象以及原因分析都与 c1时非常相似,不同的是c2直接对全局寻优而不是历史寻优起作用。
实际上,c1和c2的作用是相互交织的,历史寻优的效果和全局寻优的效果是相互影响的。
3.2 惯性权重系数
由式(1)可以看出,ω决定了对前一速度值继承的程度。它影响粒子的搜索能力并影响搜索的精细程度。
笔者在其他参数取值相同(c1=c2=1.0,粒子个数取5个,收敛标准取0.00060842)的条件下,含水层参数取值范围为 0.93 m2/min≤T≤3.72m2/min,0.002≤S≤0.005,0.0016 m-1≤1/B≤0.0033 m-1时,对 0.5≤ω≤1.0和0≤ω≤0.5分别进行3次试算,输出每个粒子目标函数值随迭代次数增加的变化。通过试算观察到这样的现象:当 ω较大(0.5≤ω≤1.0)、迭代次数达到1000次以上时各粒子的目标函数值仍有较大变化,即粒子仍保持搜索能力,3次运算的最终目标函数值分别稳定于0.00062041,0.00061140,0.00061102;当 ω较小(0≤ω≤0.5)、迭代次数不到1000次时各粒子已经基本停滞,3次运算的最终目标函数值分别稳定于0.00110930,0.00066110,0.00064549。产生上述现象的原因是,ω值越大,前一速度对当前的速度贡献越大,当粒子聚集到个体极值和全局极值附近时,式(1)中c1rand1[pik(t)-xik(t)]+c2rand2[pgk(t)-xik(t)]变得很小,这样 ωvik(t)项就成为新速度的主要部分;如果 ω很小,那么新的速度就会迅速变小,导致粒子活动范围越来越小,全局搜索能力降低。但有研究认为,ω较小时可增强局部搜索能力[3]。
4 结 语
文中将PSO算法应用于分析第1类越流系统含水层中的抽水试验数据,并确定含水层的参数。通过对数值试验结果的初步分析讨论,可以得出:①PSO算法原理简单,易于编程运算,计算结果精度不受人为影响;②PSO算法的计算结果精度高,可靠性强;③学习因子c1,c2和惯性权重系数 ω综合影响着粒子的活跃程度,进而影响粒子群的搜索能力;④建议算法控制参数取值为 c1=c2=2.0,ω由0.9随迭代次数线性递减至0.4。总之,PSO算法不失为一种分析抽水试验资料、确定第1类越流系统含水层参数的有效方法。
[1]KENNEDY J,EBERHART R C.Particle swarm optimization[C]//Proceedings of IEEE International Conference on Neural Networks.Piscataway:IEBE Service Center,1995(4):1942-1948.
[2]DOROGO M,MANIEZZO V,COLORI A.Ant system:optimization by a colony of cooperating agents[J].IEEE Trans on System,Man,and Cybernetics,1996,26(1):28-41.
[3]范娜,云庆夏.粒子群优化算法及其应用[J].信息技术,2006(1):53-56.
[4]邓显羽,彭勇,叶碎高,等.粒子群算法在水库(群)优化调度研究中的应用综述[J].水利水电科技进展,2010,30(5):90-94.
[5]向波,纪昌明,罗庆松.免疫粒子群算法及其在水库优化调度中的应用[J].河海大学学报:自然科学版,2008,36(2):198-202.
[6]王伟,王连庆.基于粒子群仿生算法的混凝土坝变形预报模型[J].水利水电科技进展,2008,28(4):11-14.
[7]张娟娟.智能优化算法在含水层参数反演中的应用[D].西安:长安大学,2006.
[8]陈崇希,林敏.地下水动力学[M].武汉:中国地质大学出版社,1999:70-122.
[9]杨天行,傅泽周,刘金山,等.地下水向井的非稳定流动的原理与计算方法[M].北京:地质出版社,1980:195-199.
[10]U.S.Department of the Interior(USDI).Ground watermAnual[M].Washington,D.C.:Bureau of Reclamation,1981:121-127.
