一种新的径流过程随机模拟方法
2011-05-03周研来梅亚东张代青
周研来,梅亚东,张代青
(武汉大学水资源与水电工程科学国家重点实验室,湖北 武汉 430072)
水文随机模拟[1-2],是指根据水文系统观测资料的统计和随机变化规律,建立能预估系统未来水文情势的随机模型,由随机模型通过统计试验获得大量的模拟序列,再进行水文系统分析计算,解决系统的规划、设计、运行与管理问题的方法。水文随机模拟技术的关键是建立合理可靠的随机水文模型。目前,国内外研究的随机水文模型主要包括回归类模型[3]、解集类模型[4]、非参数类模型[5-6]和非线性类模型[7-9]等。Sharma等[5]用核密度估计方法估计序列的条件分布,在核函数选为高斯函数时导出了基于非参数方法进行随机模拟的NP(1)模型。王文圣等[6]又将NP(1)模型推广到单变量和多变量的多阶情形,即NP(p)模型,并研究了模型在径流模拟中的可行性。肖义等[10]和张涛等[11]就洪水特征变量间的相关性基于Copula函数提出了一种洪水过程随机模拟方法。闫宝伟等[9]建立了基于Copula函数的一阶季节性随机模型,尝试将其应用于径流的随机模拟,所建模型能较好地保持原序列的偏态特性、非线性相关性和概率密度特征等统计特性。一阶自回归模型[3]和典型解集模型[4]由于构造简单,在水文模拟中备受青睐,为避开一阶自回归模型和典型解集模型中对水文序列的正态转化(该过程难免会出现部分信息失真),笔者尝试用Copula函数构造一种新的径流过程解集随机模型,即先用Copula函数构造年径流量与最大月径流量之间的联合分布,通过联合分布达到随机模拟年径流量的目的,再优选实测径流过程,将年径流量分解为各分量的径流过程。
1 基于Copula函数的解集随机模型
1.1 Copula函数的构造
Copula函数是定义域为[0,1]均匀分布的多维联合分布函数,由Sklar定理可以将多个随机变量的分布函数连接起来构造联合分布,对于二维情况,可以表述为[8,12]
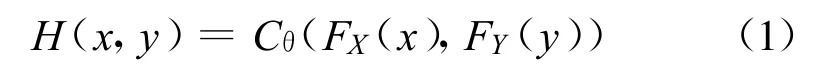
式中:H(x,y)为随机变量X和Y的联合分布函数;Cθ为参数为θ的Copula函数;FX(x),FY(y)分别为随机变量X和Y的边缘分布函数。
Copula函数在多变量水文分析计算中的应用及研究进展,文献[12]已有详细介绍。
径流过程的2个特征量(最大月径流量和年径流量)具有一定的相关性。两变量耿贝尔联合(Gumbel-Hougaard Copula)函数可用于描述具有上尾相关特性多变量之间的相关关系[13]。例如它可以很好地描述当一个变量增幅较大时,另一个与之存在相关性的变量随之明显增大的多变量相关关系[10]。基于Gumbel-Hougaard Copula函数的数学特性,采用该函数来描述最大月径流量和年径流量,其数学表达式为[8,10,13]
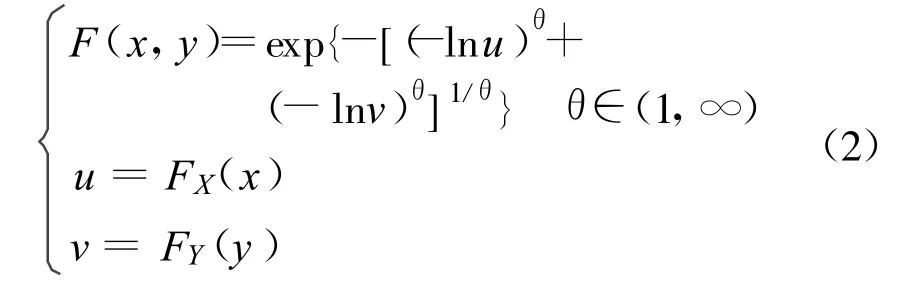
式中:FX(x)和FY(y)均为PⅢ型分布函数;θ越大,说明u,v的相关性越强,θ的估计见文献[9]。
1.2 模型算法
许多水文要素是累加而成的,如年水量是由月水量累加而得,15 d洪水总量是由15 d的日洪水量累计而得。一般而言,将各分量累加起来的总量叫做聚集;反之,从总量中可以分解出分量。解集随机模型的实质在于将总量随机解集成各分量,其显著的特点在于保持水量平衡,即各分量的水量相加严格等于总水量。Copula函数对最大月径流量 X和年径流量Y进行联合描述,通过联合分布的随机抽样方法对存在相关性的最大月径流量和年径流量成对地取样,从而达到随机模拟最大月径流量和年径流量的目的。参照文献[12]的峰量随机抽样方法以及典型解集模型[14]得出基于Copula函数的解集随机模型模拟径流过程的步骤如下:
步骤1 根据最大月径流量和年径流量的联合分布可以得到当最大月径流量为某指定值时年径流量的条件分布:

步骤2 产生服从[0,1]均匀分布的2个独立随机数r1和r2。
步骤3 令r1为最大月径流量发生的不超过x值的概率FX(x),即 u=FX(x)=r1,根据 x=(u)得到x值。
步骤4 令r2为最大月径流量X=x时年径流量y的条件概率分布值,即r2=CX(y X =x),从而可根据y=(r2X=x)计算得到 y。
步骤5 由步骤3和步骤4即可抽取1对最大月径流量和年径流量的组合(x,y)。
步骤6 以模拟的最大月径流量和年径流量组合(x,y)为控制条件,选择最大月径流量和年径流量的比值与x/y值接近的实测径流过程,并采用解集[11]方法进行分解,得到模拟的径流过程:

式中:Xi(t),xi(t)分别为第i年第t个截口的模拟径流值和实测径流值;Yi为第i年的模拟年径流量;A为将年径流量(亿m3)转换为总流量(m3/s)的单位换算系数;Ki(t)为第i年第t个截口的分解系数。
步骤7 重复步骤2至步骤6共M次,即可模拟出M年的径流过程。
2 模型应用研究
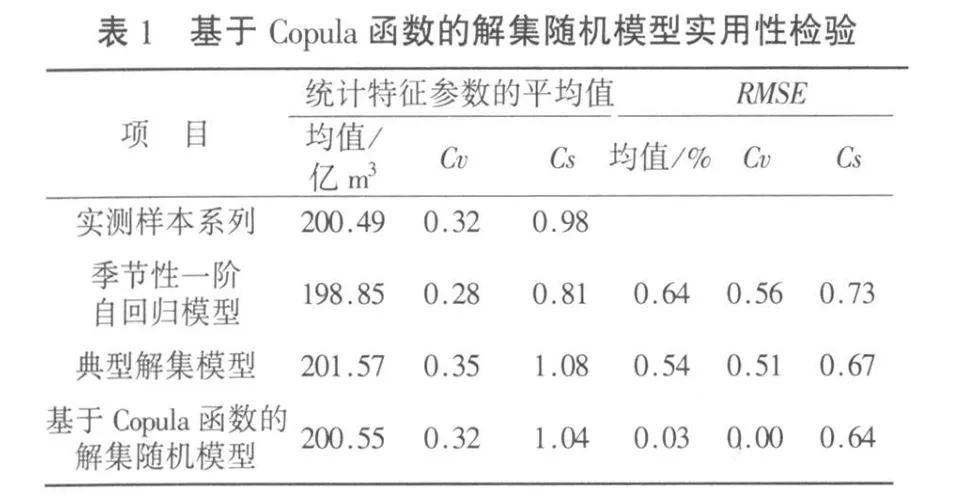
利用黄河中上游河口镇水文站1919—1988年共70年的实测月径流量资料,检验基于Copula函数的解集随机模型的可行性和有效性。由于所选资料序列较长,某种意义上可以代表整体的统计特性,以此来验证模型,可信度较高。同时选取季节性一阶自回归模型和典型解集模型作为对照,以说明本文所建模型的实用性。
在实测径流资料中,每年选择1对最大月径流量和年径流量数据,构成样本容量为70的联合观测值系列,并据此建立最大月径流量X和年径流量Y的两变量联合分布。X和Y的边缘分布采用PⅢ型分布,分别为FX(x)和 FY(y),采用线性矩法估计FX(x)和FY(y)的参数,得到实测年径流量的统计特征值,见表1。将估计的参数假定为河口镇站最大月径流量和年径流量总体分布的参数。依据Kendall秩相关系数和Copula函数的参数 θ的解析关系[8,12],得到最大月径流量和年径流量的参数θ=4.25。图1为联合观测值的经验分布和理论分布的相关关系。据图1可知,θ=4.25时,最大月径流量和年径流量联合观测值的经验分布和理论分布拟合较好,θ=4.25可作为联合总体分布的参数估计量,所建立的X和Y的联合分布是合理的。由Sklar定理及式(2)得到X和Y的联合分布F(x,y):
?

图1 联合观测值经验分布和理论分布的比较
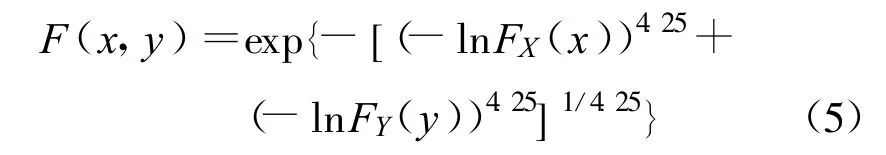
绘制最大月径流量和年径流量的两变量联合分布函数及概率密度函数三维图,如图2、图3所示。
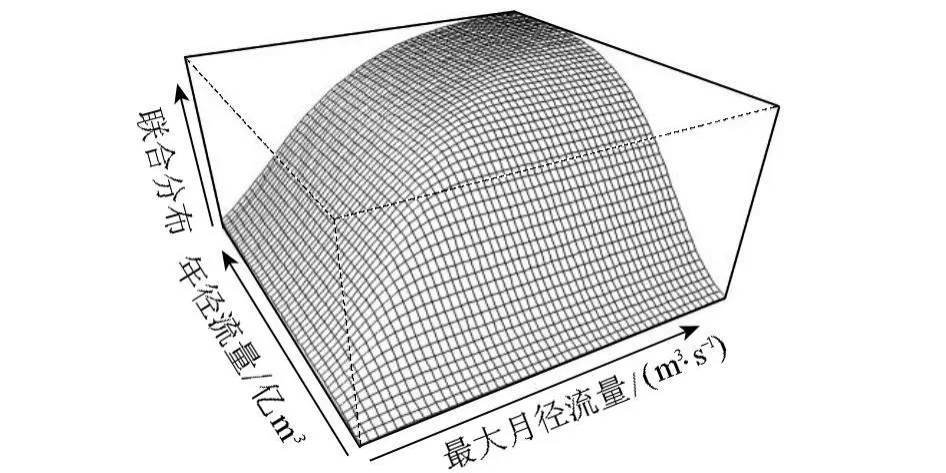
图2 X和Y的联合分布函数

图3 X和Y的联合概率函数
此外,从联合分布随机抽取7万对最大月径流量和年径流量数据,点绘得到它们的频率散点图,如图4所示。由图4可见,当模拟的最大月径流量为某一频率时,可能发生多种频率的年径流量,最大月径流量和年径流量之间不存在严格的一一对应关系;从回归关系和相关关系来看,最大月径流量和年径流量频率的回归系数为0.92,相关系数为0.85,说明最大月径流量和年径流量组合既存在较好的同频率特性又存在一定的随机性;从频率分布状况来看,最大月径流量和年径流量偏小值的频率居多,中等值的频率次之,而较大值频率分布较少,这与水文要素的枯、平、丰水年的频率分布状况十分吻合。
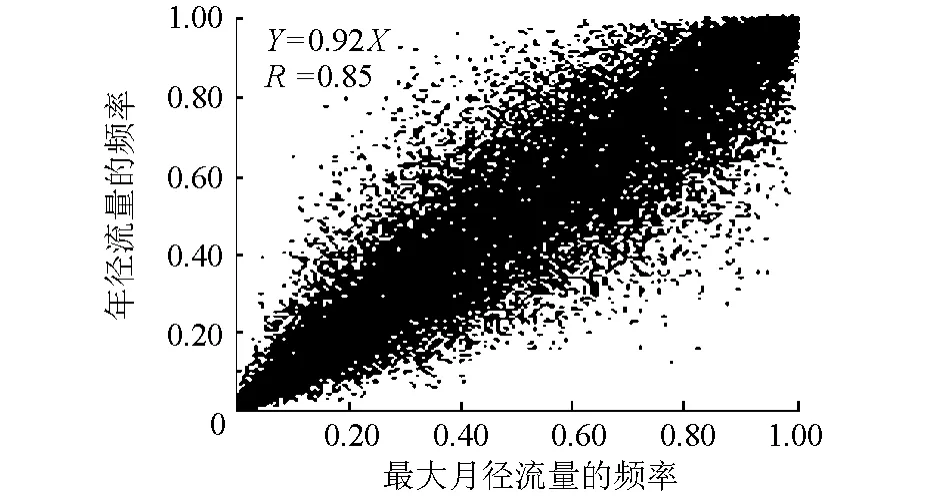
图4 随机模拟X和Y频率的散点图
根据图4中任意一点对应的最大月径流量和年径流量,可求得最大月径流量与年径流量的比值,依据该比值选择具有相似最大月径流量与年径流量之比的实测径流过程,采用典型解集方法进行分解,模拟多年月径流过程(如7万年),其年径流量的统计参数见表1。
统计分析河口镇水文站1919—1988年实测的月径流过程资料,可知1967年为丰水年(最大月径流量为3401m3/s,年径流量为420亿m3),见图5。图5还给出了以1967年实测月径流过程为基础进行缩放后得到的2条月径流过程线。由图5可见,模拟的径流过程在形状上与实测过程十分相似。因此,随机模拟的径流过程系列能够反映实测径流的形状。
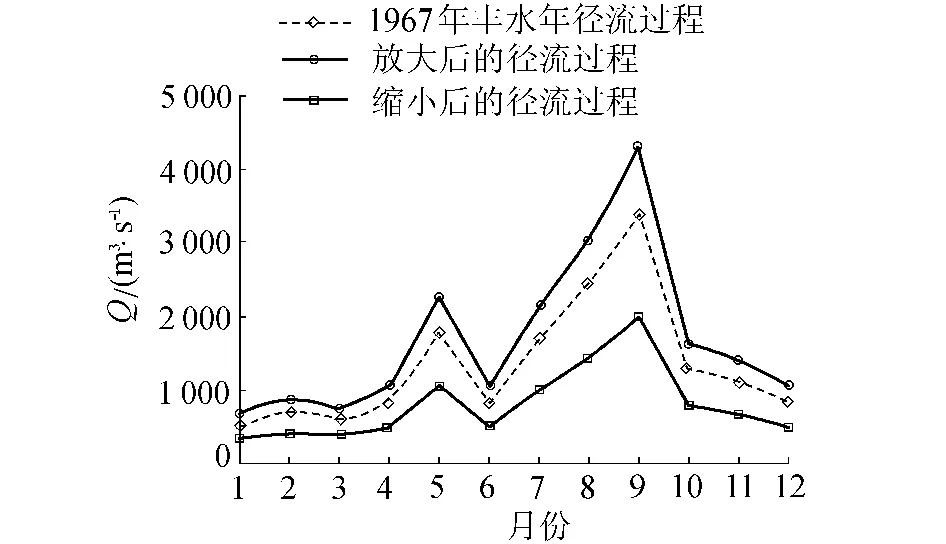
图5 以1967年实测径流过程模拟的径流过程线
对基于Copula函数的解集随机模型是否能很好地保持实测系列的年径流量统计特征进行检验,并与水文领域常用的季节性一阶自回归模型和典型解集模型[14]进行比较。对于每个模型,在其模拟的径流过程系列对应取出7万个年径流量,分别组成1000个样本容量为70的年径流量样本。对每个年径流量样本分别估计统计特征参数(均值,Cv和Cs),并分别计算统计特征参数的均值。采用综合相对均方误差RMSE[9-10]作为模型评价指标:

评价指标RMSE的值越小,说明随机模型越能够保持实测系列的统计特征。表1给出了实测系列和模拟系列的年径流量统计特征值及评价指标值。由表1可知,季节性一阶自回归模型模拟径流过程的年径流量统计特征效果相对较差;基于Copula函数的解集随机模型的RMSE均低于季节性一阶自回归模型和典型解集模型的RMSE。究其原因,基于Copula函数的解集随机模型避开了季节性一阶自回归模型和典型解集模型中对水文序列的正态转化(难免会出现部分信息失真),而是直接随机模拟年径流总量,然后选用实测径流过程分解为模拟的径流过程,因此能够很好地保持实测系列的径流过程形状及年径流量的统计特征。
3 结 语
构造了最大月径流量和年径流量的联合分布,采用基于联合分布的随机抽样方法模拟了大样本的径流过程,从而提出了一种新的径流过程随机模拟方法,建立了基于Copula函数的解集随机模型。该模型避开了季节性一阶自回归模型和典型解集模型中对水文序列的正态转化和相依形式的主观假定,很好地考虑了最大月径流量和年径流量之间的相关性及两者频率组合的随机性,选用实测径流过程作为随机模拟径流过程的时程分配形式,能很好地保持实测系列的径流过程形状及年径流量的统计特征。实例计算结果表明,基于Copula函数的解集随机模型的模拟效果至少可以与常用的典型解集模型相当,适用于水文时间序列的随机模拟,从而为水文水资源的随机模拟提供了一种新途径。
[1]芮孝芳,刘方贵,邢贞相.水文学的发展及其所面临的若干前沿科学问题[J].水利水电科技进展,2007,27(1):75-79.
[2]胡庆芳,王银堂,刘克琳,等.基于改进的两参数月水量平衡模型的月径流模拟[J].河海大学学报:自然科学版,2007,35(6):638-642.
[3]葛朝霞,王会容.黄河上游月径流量与海温的关系研究[J].河海大学学报:自然科学版,2003,31(6):605-608.
[4]KOUTSOYIANNIS D,MANETAS A.Simple disaggregation accurate adjusting procedures[J].Water Resources Research,1996,32(7):2105-2117.
[5]SHARMA A,TARBOTON D G,LALL U.Streamflow simulation:a nonparametric approach[J].Water Resources Research,1997,33(2):192-308.
[6]王文圣,丁晶.基于核密度估计的多变量非参数随机模型初步研究[J].水利学报,2003,34(2):9-14.
[7]PRAIRIE J R,RAJAGOPALAN B,FULP T J,et al.Modified K-NN modelfor stochastic streamflow simulation[J].Journal of Hydrologic Engineering,2006,11(4):371-378.
[8]SALVADORI G,de MICHLELE C.Frequency analysis via copulas theoretical aspects and applications to hydrological events[J].Water Resources Research,2004,40(12):1-17.
[9]闫宝伟,郭生练,刘攀,等.基于Copula函数的径流随机模拟[J].四川大学学报:工程科学版,2010,42(1):5-9.
[10]肖义,郭生练,熊立华,等.一种新的洪水过程随机模拟方法研究[J].四川大学学报:工程科学版,2007,39(2):55-60.
[11]张涛,赵春伟,雒文生.基于Copula函数的洪水过程随机模拟[J].武汉大学学报:工学版,2008,41(4):1-4.
[12]郭生练,闫宝伟,肖义,等.Copula函数在多变量水文分析计算中的应用及研究进展[J].水文,2008,28(3):1-7.
[13]NELSON R B.An introduction to Copula[M].New York:Springer,1999.
[14]中华人民共和国能源部,中华人民共和国水利部.水利水电工程设计洪水计算手册[M].北京:中国水利水电出版社,2001.
