聚丙烯腈纤维路面高强混凝土疲劳性能分析

杨启斌，罗素蓉

(1.福建工程学院，福建 福州 350108;2福州大学土木工程学院，福建 福州 350108)

0 前言

随着国民经济的发展，公路交通运输呈现出“大流量、重型化”的特点，导致相当一部分的新建路面遭受不同程度的破坏，这对水泥混凝土路面提出了新的要求。实践证明，在高等级尤其是重交通道路上，原有的低强度的混凝土已经不能适应交通发展要求。但随着混凝土强度的提高，其脆性大，延性较差的缺点也更加突出。纤维作为一种传统的纺织材料，掺入混凝土中可以改善混凝土的品质［1-5］。在混凝土中掺入合成纤维能显著提高混凝土的抗裂性、抗渗性、抗冻性、抗冲击性等，使混凝土的综合性能大幅度提高［6-7］，在公路路面、机场道面上开始应用合成纤维混凝土［8］。

目前关于聚丙烯腈纤维增强混凝土的研究多集中在静力性能方面，且多集中在低强度混凝土上，在动载作用下的高强混凝土疲劳特性研究成果较少。考虑到路面高强混凝土通常承受随机或周期性反复荷载作用，因此准确地预估混凝土路面的疲劳寿命是水泥混凝土路面结构设计的核心。

本文研究了不同掺量下聚丙烯腈纤维高强混凝土的抗折强度以及纤维混凝土的疲劳寿命，在试验研究的基础上，利用三参数Weibull分布理论研究了不同掺量下聚丙烯腈纤维高强混凝土的疲劳寿命分布规律，建立了纤维混凝土的弯曲疲劳方程，为路面设计提供参考依据。

1 疲劳试验方案设计

1.1 混凝土试件

疲劳试验采用混凝土试件为100×100×400 mm3的小梁，分4批成型共44根小梁。每组配合比分别制作11个试件，其中3个试件用于测定弯拉强度，8个试件用于测定疲劳强度。结合路面混凝土的特点，按28 d弯拉强度6.0 MPa作为设计配合比的控制指标，混凝土设计强度等级为C60，粉煤灰等量取代水泥，采用配合比为C:W:S:G:F=1:0.39:1.84:2.76:0.33。选用路威聚丙烯腈纤维，纤度为1.5，标称直径为12.7 μm，长度为12 mm，比重为1.18×103kg/m3。聚丙烯腈纤维直接外掺于混凝土内，由于纤维的掺入，使得混凝土的坍落度有一定的损失，通过适当增加减水剂来控制混凝土坍落度，使混凝土满足工作性的要求，配合比及工作性如表1所示。

表1 混凝土配合比及工作性Table 1 Mix proportion of concrete

1.2 试验装置

试验分静载试验和疲劳试验两部分，均采用英国Instron公司生产的Instron 1342电液伺服疲劳试验机。采用三分点加载方式(如图1所示)，以保证梁试件底面有一段弯矩相等的均匀受拉区，两支点间距100 mm。加载波形统一采用正弦波，它基本接近路面上行车作用的实际波形，加载波形如图2所示。循环特征值R为:

式中:Pmin、Pmax分别为作用在试件上的最小荷载和最大荷载(KN)。

水泥混凝土路面常规结构在一般行车荷载作用下的应力水平范围为0.2～0.65之间，但随着交通运输业的发展，重载超载现象变得越来越普遍，在面板较薄的水泥混凝土路面，有些荷载作用下的应力水平可达到0.85，甚至出现极限破坏。考虑较大应力水平时疲劳试验数据离散性较大，疲劳试验时应力水平选取了较大且试验数据相对稳定的0.80，R取0.10，试验的加载频率为5 Hz。

2 疲劳试验结果

根据试验结果，各批试件的抗折强度试验结果如图3所示，加入聚丙烯腈纤维后，在抗折试验中，纤维高强混凝土的总体破坏荷载略有提高，但提高比例有限。这主要是由于聚丙烯腈纤维属于低弹性模量、高延伸率的聚合物纤维，将其掺入高强混凝土后，其抗折强度提高幅度并不多。

在疲劳加载过程中，各个试件破坏前跨中挠度都比较小，裂缝一旦出现，便迅速扩展到全截面，破坏具有一定的脆性，且破坏面几乎发生在均匀受拉区域。随着纤维掺量的提高，脆性破坏得到一定的缓解，具备一定的延性特征。

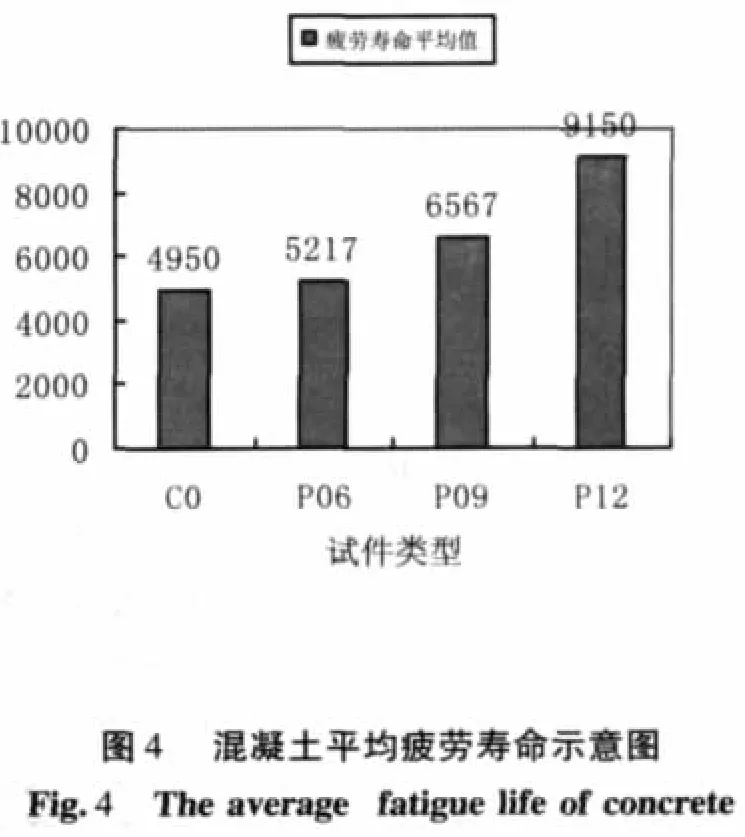
疲劳试验结果如表2所示。由于混凝土的不均质性以及试验状况和强度变异的影响，无论是高强混凝土还是聚丙烯腈纤维高强混凝土的疲劳试验结果，均有一定的离散性。由图4可以看出，随着纤维掺量的提高，混凝土的疲劳寿命呈现不同程度的增长，说明纤维的掺入对提高高强混凝土的疲劳寿命是有效的。纤维的掺入，降低了高强混凝土的脆性，提高了韧性，高效减水剂和粉煤灰的掺入，又使得水泥石的孔结构得到改善，匀质性增加，密实度和强度大大提高，且界面区结构密实，不均匀性减小，水泥石与集料之间的粘结性得到加强。因此，纤维高强粉煤灰路面混凝土较高强混凝土有较高的疲劳寿命。

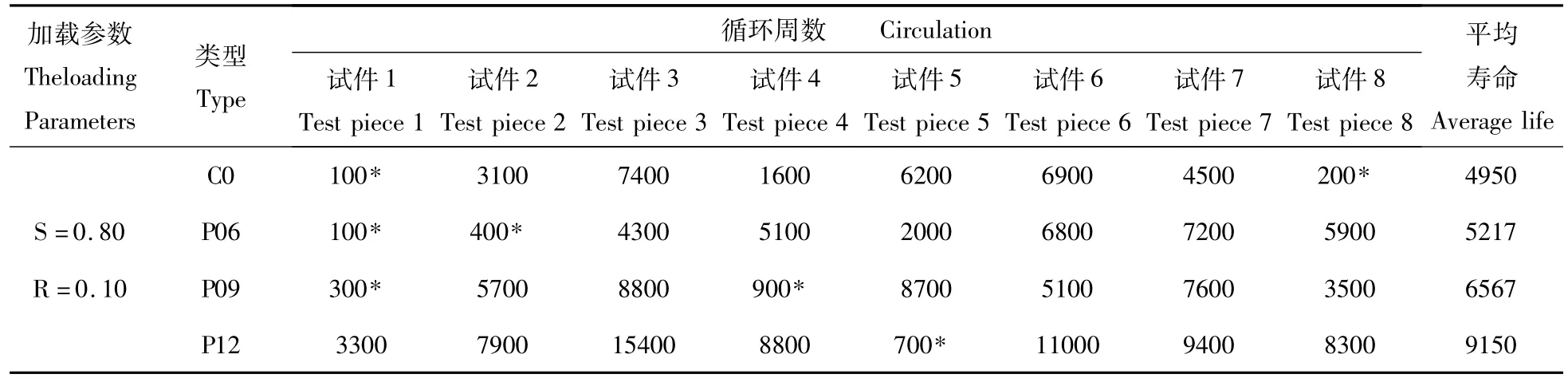
表2 疲劳试验结果Table 2 Statistical results for the bending fatigue tests

3 疲劳性能分析

混凝土的疲劳寿命是一个随机变量，从表1可以看出其离散性较大。为了最大限度地降低离散性对疲劳试验结果的影响，需要研究其概率分布，才能较为准确、全面建立疲劳方程。适合表达疲劳寿命分布的有正态频率函数、威布尔频率函数。近年来双参数威布尔频率函数越来越为研究疲劳性能的研究人员所看重［9-11］。已有研究表明，混凝土疲劳寿命服从双参数威布尔分布［12-13］，但有关三参数Weibull分布规律的验证还比较少，有必要进一步深入研究纤维高强混凝土的三参数威布尔分布规律。

3.1 威布尔分布的三参数估计

文献［14］基于疲劳寿命既服从对数正态分布，又服从威布尔分布这样的前提，从概率论中特征函数方面研究两个分布的逼近性，得到两个分布参数之间的关系式，在理论上沟通了两分布的联系，这样就可以利用对数正态分布的参数去估计威布尔分布的参数，从而得到一种新的三参数威布尔分布的估计方法。

首先，随机变量X服从对数正态分布，有密度函数

式中，μ为均值，σ2为方差。

同时，随机变量X又服从威布尔分布，有密度函数

式中，m为形状参数，α为尺度参数，γ为位置参数。

由文献［14］得到威布尔分布(m，α，γ)与对数正态分布(μ，σ2)之间的逼近表达式，也就是(m，α，γ)和(μ，σ2)之间的关系:

式中，λ =ασ2/logαe，Q=αμ(μ =σ2是以 α 为底的对数正态分布中的参数)。

式中，Γ(x)为伽玛函数。

由W1(m)、W2(m)和W3(m)三个特殊函数的曲线性质可知，他们都是m的单调函数，那么由对数正态分布的(μ，σ2)可唯一求出λ、Q，由式(8)可唯一求出W1，再由W1(m)曲线可唯一求得m，最后由式(8)、(9)可唯一求出α和γ。将威布尔分布的逼近性参数估计方法的计算列于表3～4。

表3 计算流程的相关参数值Table 3 Relevant indexes of various series of tests

表4 对数正态分布参数值及威布尔分布逼近性参数Table 4 Distribution parameter of test specimen

3.2 三参数威布尔分布疲劳寿命

表5 三参数威布尔分布疲劳寿命NTable 5 The fatigue life of three-parameter Weibull distribution

3.3 三参数威布尔分布P-N方程

表6 三参数威布尔分布回归方程Table 6 The fatigue equations of three-parameter Weibull distribution

由试验数据的回归分析可以看出，相关系数R2均在［0.9989～0.9994］以上，表明存活率P与疲劳寿命N之间相关性显著，因此可认为纤维高强混凝土疲劳寿命服从三参数威布尔分布规律。

4 结论

(1)随纤维掺量的提高，纤维高强混凝土的抗疲劳性能比高强混凝土的抗疲劳性能显著提高，表现出优异的抗疲劳性能。

(2)用三参数Weibull分布验证了聚丙烯腈纤维高强混凝土的概率分布，证明其疲劳寿命概率分布可以用Weibull分布理论来描述。

(3)根据试验数据回归出了聚丙烯腈纤维高强混凝土的疲劳寿命方程，相关性显著。

［1］ 邓宗才.高性能合成纤维混凝土［M］.北京:科学出版社，2003

［2］ 谢 晶.不同纤维对SMA疲劳性能的影响［J］.公路，2008(10):214-217

［3］ 俞家欢，贺改先，赵复笑，等.素混凝土与纤维混凝土疲劳性能的研究［J］.沈阳建筑大学学报，2007(5):397-401

［4］ 曲旭光，史宝华，彭洪波，等.聚丙烯腈纤维混凝土性能试验研究［J］.混凝土，2009(4):81-82

［5］ 孙凌寒，邵国建，黄俊，等.短碳纤维局部增强混凝土疲劳性能实验研究［J］.实验力学，2009，24(5):445-452

［6］ 陈建奎.混凝土外加剂的原理与应用(第二版)［M］.北京:中国计划出版社，2004

［7］ 李建辉，张科强，邓宗才，等.粗合成纤维混凝土抗弯冲击强度的分布规律［J］.建筑科学与工程学报，2007，24(4):54-59

［8］ 岑国平，朱志远，王硕太，等.道面合成纤维混凝土性能的试验与比较［J］.混凝土，2008(6):45-46

［9］ 高镇同，熊峻江.疲劳可靠性［M］.北京:北京航空航天大学出版社，2002

［10］ 姚国文，黄培彦.循环荷载下纤维薄板增强RC梁的疲劳性能研究［J］.土木工程学报，2006(4):35-38

［11］ 马国强，岑国平，王硕太，等.合成纤维混凝土路面切割小梁弯曲疲劳试验［J］.公路，2007(7):214-217

［12］ CHEN Shuan-fa，ZHENG Mu-lian，Wang Bing-gang.Formulation and application of fatigue equation for porous concrete［J］.Journal of the Chinese ceramic society，2005，33(7):827-831

［13］ 郑木莲，孙家伟，王秉纲.贫混凝土疲劳方程的建立及其应用研究［J］.西安建筑科技大学学报，2007(1):92-97

［14］ 曾 攀.材料的概率疲劳损伤特性及现代结构分析原理［M］.北京:科学技术文献出版社，1993