土石坝低弹性模量混凝土防渗墙应力变形数值分析

马晓华， 梁国钱， 郑敏生， 徐长节， 牟 儒

（1.浙江省水利河口研究院浙江省水利防灾减灾重点实验室，浙江 杭州 310020；2.浙江大学软土与环境工程教育部重点实验室，浙江 杭州 310027）

0 前言

混凝土防渗墙作为一种防渗结构，对保证地基稳定和大坝安全有着极其重要的作用，且具有施工工艺简单、工期短、防渗效果好等优点，在国内外土石坝的防渗加固工程中应用广泛。根据墙体弹性模量的不同，可分为刚性混凝土防渗墙和塑性混凝土防渗墙，前者的刚度远大于周围土体，与周围填土的变形差异较大，从而导致自身的应力较大，易出现开裂甚至压碎等现象，寿命得不到有效保证；后者刚度与周围土体较为接近，变形协调性好，承受的应力较小，结构的整体性能较好保持，防渗效果好，但需要处理好强度较低的问题。针对二者的优缺点，现在越来越多的防渗墙采用低弹性模量混凝土，其弹性模量介于2 000～3 000 MPa之间，能很好地兼顾强度与应力两方面要求，具有较高的应用价值[1]。

在防渗墙与周围土体的接触面模拟中，常用的接触面单元主要包括古德曼 （Goodman）[2]和德塞 （Desai）[3]接触面单元，应用得最多的还是Goodman单元。但Goodman单元在使用中存在以下问题，即受压时两侧的单元可能相互嵌入，且由于其法向弹性系数取值很大，求解的法向位移若出现很小偏差就能导致法向应力有较大出入，导致计算的结果误差较大。

在防渗墙数值模拟研究中，沈新慧[4]（1995年）在研究防渗墙及其周围土体的应力时，防渗墙按线弹性材料考虑，当应力接近混凝土强度时，考虑材料的弹塑性。朱国甫[5]（1995年）等用有限元法分析研究三峡二期围堰高双墙方案时，对基岩面以上混凝土采用米赛斯 (Von-Mises)弹性理想塑性模型，屈服应力取为混凝土的抗压强度，基岩面以下混凝土采用线弹性应力应变关系。沈珠江[6]（1996年）等在对三峡二期高土石围堰作应力应变分析时，采用低双塑性墙方案，结果表明对改善墙体应力状态有利，塑性墙内的压应力和拉应力均大大低于刚性墙，墙内最大压应力和拉应力均随着墙厚的增大而减小。朱俊高[7]（1997年）等在土石坝的有限元计算中，引入适合于混凝土材料的椭圆—抛物双屈服面弹塑性模型。对处于低应力水平状态的混凝土，不必使用弹塑性模型；对于应力水平较高的混凝土结构，采用弹塑性模型时的计算应力比弹性模量取为常量时的计算应力小，更为合理；对塑性混凝土，应采用弹塑性本构模型。

虽然国内外学者对刚性和塑性混凝土防渗墙的应力变形已经做了大量研究工作，但目前在大坝除险加固过程中应用较多的低弹性模量混凝土防渗墙的工作性状及受力特性、低弹性模量混凝土材料的特性等方面的研究的较少。因此，有必要对低弹性模量混凝土防渗墙进行深入研究，为采用低弹性模量防渗墙处理水库大坝提供重要技术支持。本文对采用低弹性模量混凝土防渗墙加固的某土石坝典型断面进行了有限元数值分析，计算分析了在不同水位下低弹模混凝土防渗墙的应力变形情况，并将数值计算得到的水平位移值与实测值进行了对比。另外，还对比分析了不同弹模下防渗墙墙体的位移和应力的变化情况，可供实际加固工程中防渗墙弹性模量取值参考。

1 工程概况

某土石坝为扩大黏土心墙砂壳坝，坝顶高程37.6 m，最大坝高26.6 m，坝顶宽10 m，底部最大宽度119.29 m，坝体填土为含砾黏土和砂砾料，坝基从上到下依次为砂壤土层、砂砾石层、砂质黏土层、凝灰质粉砂岩。大坝已运行40多年，存在不少安全隐患，如坝体填筑质量较差，坝基渗透变形和大坝下游面抗滑稳定不符合要求等，故采用了低弹性模量混凝土防渗墙对该土石坝进行了除险加固处理。防渗墙厚80 cm，布置在坝轴线上游3.55 m处，底部深入弱风化层即凝灰质粉砂岩层0.5 m，弹性模量为2 100 MPa。大坝加固后的断面见图1。数值计算参数见表1。

2 计算模型

2.1 模型概况

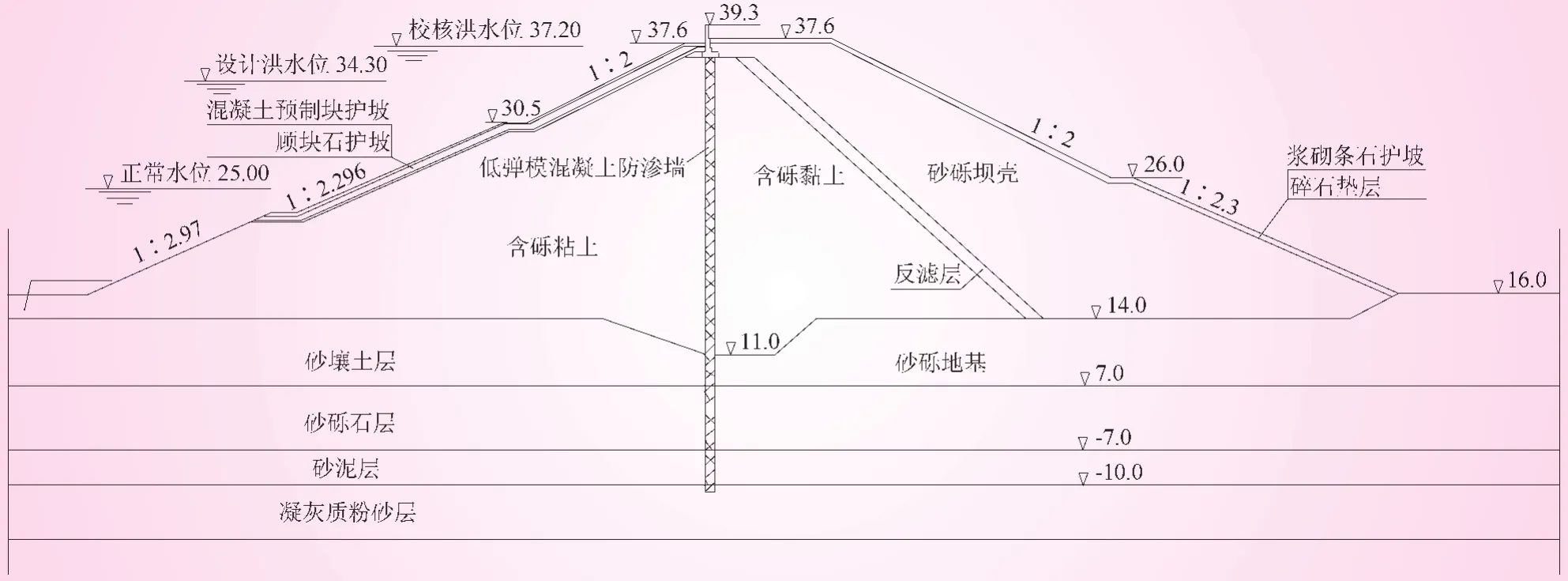
图1 大坝加固后典型断面 （高程：m）

防渗墙计算时按平面应变问题考虑，计算范围自坝趾和坝踵分别向上下游延伸100 m，整个断面划分为49 664个单元，50 377个节点，模型中坝基两端采用滑动支座，约束水平向的位移，坝基底部采用固端支座，约束一切变形。本次分析计算按加固过程中的施工进度模拟，先计算出在坝体施工水位下的水荷载以及坝体和坝基土重力荷载作用下的应力场，作为坝体加宽完毕时的状态的应力场，再在坝体中打入防渗墙，重新计算坝体的应力应变。由于坝体运行时间较长，认为坝体和坝基土固结已完成，另外根据低弹模混凝土的无侧限抗压试验成果，防渗墙、坝体及坝基均采用线弹性 （E-μ）模型。

表1 计算参数

2.2 坝体和防渗墙接触面Goodman单元修正

Goodman单元[2]在接触面的模拟中运用十分广泛。它是一种无厚度的4节点单元，该单元由2片长度为L的接触面12和34组成，两接触面之间由无数微小的弹簧连接，每对弹簧含有法向弹簧和切向弹簧，分别用来表示法向和切向的变形和应力情况。对于实际工程中由于材料不同等可能出现的接触面摩擦力变化的情况，运用Goodman单元可以通过改变切向弹簧的弹性系数来轻松实现，而对于实际接触面受压时不会发生相互嵌入的情况，Goodman单元则通过将法向弹簧的弹性系数取一个较大的数值来实现。但这也是Goodman单元最大的缺陷，即无论法向的弹性系数取多大，受压的时候总是会使两侧的普通单元相互嵌入，并且由于法向的弹性系数取值很大，如果计算中法向位移有一微小误差则将带来法向应力偏差很大[8，9]。

为克服Goodman单元的这个缺点，李守德和愈洪良[10]提出了一种改进办法，即在Goodman单元的基础上将法向的弹簧换成了刚性的连杆，单元法向受压时，法向无相对位移，法向受拉时，刚性连杆断开，单元不贡献劲度。

考虑到在防渗墙的实际施工中需要用泥浆护壁，从而使得防渗墙与周围的坝体和坝基之间留有泥皮，在模拟时采用李守德和俞洪良提出的Goodman修正单元，结合实际工程防渗墙周围泥皮的物理试验结果，并参照已有的一些资料，取摩擦系数为0.2。除了在防渗墙上下游两侧采用Goodman修正单元之外，在防渗墙的底部也采用Goodman修正单元，相当于半固定半铰接的连接方式，较单纯固定或者单纯铰接更为合理。

2.3 计算工况

根据工程实际情况，防渗墙弹性模量取为2 100 MPa，计算了正常蓄水位 （25.0 m）工况和校核洪水位 （37.2 m）工况下防渗墙墙体的水平向 （上下游方向）位移和应力。

3 计算成果分析

3.1 正常蓄水位下防渗墙水平位移

图2 正常蓄水位下防渗墙水平位移值与实测值对比

正常蓄水位条件下，防渗墙水平位移计算值与实测值对比如图2所示。从图2可以看出，防渗墙水平位移数值计算结果与实测值吻合较好；最大值出现在21～22 m高程之间，最大值约为4.3 mm，最小值出现在墙底，几乎没有位移。

3.2 正常蓄水位下防渗墙墙体上下游表面的主应力

正常蓄水位下防渗墙墙体上下游表面主应力计算成果见图3。

图3 正常蓄水位下防渗墙上下游表面主应力

由图3可知，防渗墙上下游表面的主应力曲线走向一致；整个墙体只在底部有少量地方受拉 （正为压负为拉），且应力很小，不足0.03 MPa，其余大部分墙体均受压，上游的压应力最大值约为0.20 MPa，发生在1 m高程左右，下游最大值约为0.15 MPa，发生在3 m高程左右。

3.3 正常蓄水位与校核洪水位下防渗墙的位移与应力对比

正常蓄水位与校核洪水位下防渗墙水平位移值对比见图4。

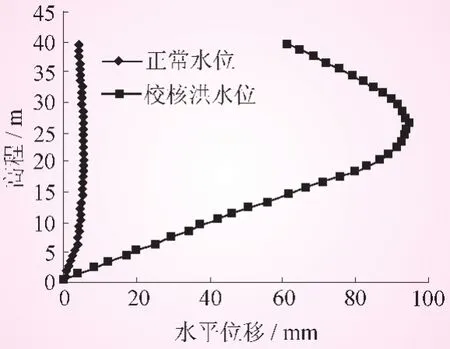
图4 正常蓄水位与校核洪水位下防渗墙水平位移值对比

由图4可以看出，校核洪水位下墙体的水平位移大幅度增加，最大值已接近100 mm，而在正常蓄水位下位移值则很小，这说明上游水位的变化对防渗墙墙体的水平位移影响很大，因此，在大坝日常运行过程中，应特别注意水位变化对防渗墙变形的影响。

正常蓄水位和校核洪水位下防渗墙上下游表面的第一主应力和第三主应力对比见图5。

图5 正常水位和校核洪水位上下游面主应力对比

从图5可以看出，由于水位的升高，防渗墙上下游表面的第一主应力和第三主应力均大幅度增大，并且有了明显的受拉区和受压区。另外，由于防渗墙相当于一根悬臂梁，受力弯曲时一侧受拉一侧受压，因此，无论是第一主应力还是第三主应力，防渗墙的上下游曲线基本呈现对称的特性。

4 结论

采用改进Goodman单元，通过建立二维有限元模型对采用低弹性模量混凝土防渗墙的某土石坝进行了数值模拟，分析了不同水位下墙体上下游的应力分布以及低弹性模量混凝土防渗墙和刚性混凝土防渗墙变形和应力的区别。通过本文数值计算分析，可得到如下的结论：

（1）防渗墙弹性模量取值为2 100 MPa时，正常蓄水位条件下防渗墙上下游表面的主应力曲线走向一致，整个墙体只在底部有少量地方受拉，且应力很小，不足0.03 MPa，其余大部分墙体受压，上游压应力最大值约为0.20 MPa。

（2）上游水位对防渗墙墙体的水平位移影响很大，水平位移值会因水位的升高而大幅度增加。同时，由于水位的升高，防渗墙上下游表面的第一主应力和第三主应力均大幅度增大，并且防渗墙出现了明显的受拉区和受压区。

（3）坝体中的防渗墙近似于一根悬臂梁，受力弯曲时一侧受拉一侧受压，故而防渗墙上下游应力曲线基本呈现对称的特性。

［1］ 蔚高洋.低弹模混凝土防渗墙在某土石坝加固中的应用［J］.浙江水利科技， 2006（2）:37－39.

［2］ Goodman R E,Taylor R L,Brekke T L.A model for the mechanics of jointed rock［J］.J.Soil Mech.and Found.,Engrg.Div,ASCE,1968,99（5）:637－660.

［3］ Desai,C.S.,Zaman,M.M.Thin Layer Element for Interface and Joints［J］.International Journal for Numerical and Analytical Methods in Geomechanics,1984,8（1）:19－43.

［4］ 沈新慧.防渗墙及其周围土体的应力探讨［J］.水利学报，1995（11）:39-45.

［5］ 朱国甫，袁建新，刘立胜.三峡工程二期围堰心墙高双墙方案有限元分析［J］.岩土力学， 1995， 16（2）:15-23.

［6］ 沈珠江，刘松涛.三峡二期高土石围堰应力应变分析研究［J］.人民长江， 1996， 27（10）:1-4.

［7］ 朱俊高，殷宗泽.高土石坝混凝土防渗墙弹塑性应力变形分析［J］.水利学报， 1997（7）:19-23.

［8］ 贾丽彬，王仲良，周悦波.土石坝防渗墙体与坝体间摩擦接触单元理论研究［J］.水利科技与经济， 2007， 13（3）:156－158.

［9］ 彭成山，张学菊.土坝防渗墙设置摩擦单元对墙体应力变形的影响［J］.华北水利水电学院学报， 2007， 28（4）:11－14.

［10］ 李守德，俞洪良.Goodman接触面单元的修正与探讨［J］.岩石力学与工程学报， 2004， 23（15）:2628－2631.