轨距不平顺激励下高速列车动力响应研究

张 新， 李向国， 王海云， 闫公甫

(石家庄铁道大学土木工程学院，河北 石家庄 050043)

0 引言

轨距是铁路线路基本参数之一，轨距的正确与否对机车车辆的安全运行、乘客的旅行舒适度、设备的使用寿命和养护费用起着决定性的作用。轨距不平顺是由于左右两股钢轨横向偏移而引起的轨距变化［1］。为研究轨距不平顺对列车运行的影响，通过建立不同工况的轨距不平顺，采用仿真软件，模拟车辆在有轨距不平顺的轨道上运行。通过对不同工况轨距不平顺下仿真计算结果的分析，深入了解轨距不平顺对列车运行的影响，为轨道维修管理人员提供了一定的参考依据。

1 机车车辆对轨道不平顺动力响应的仿真计算

1.1 车辆动力仿真模型

车辆模型是由车体、转向架构架、轮对，通过一系、二系悬挂元件联接所组成的机械模型［2］。根据分析目的和模拟重点的不同，车辆模型有单轮对简化模型、转向架半车模型和整车模型。由于前两种模型由于不能反映或者不能充分反映车辆各主要部分之间的相互耦合的影响叠加作用，因此本文采用整车模型。车辆系统中除弹性、阻尼元件外的各个部件，如车体、构架、轮对等都视为刚体。一个刚体有6个自由度，分别沿3个坐标轴的线位移和绕3个坐标轴的转动位移，分别对应伸缩、横移、沉浮、摇头、侧滚、点头等6种基本振动形式。

1.2 轨道模型

在轨道模型中，钢轨作为弹性连续梁处理，梁与下部基础在垂向上考虑为并联线性弹簧/阻尼联结，横向上考虑为串联线性弹簧/阻尼联结。采用的钢轨为中国60 kg/m标准断面新轨;轨道模型的动力学参数如图1所示。

1.3 轮轨接触模型

广义的轮轨关系包括轮轨接触几何关系和轮轨蠕滑关系［3］。求解轮轨接触几何关系是将轮轨型面进行数值化离散，根据轮轨的几何约束条件，采用最小距离法确定轮轨接触点，进而计算接触几何参数。求解轮轨相互作用力时，法向力由Hertz线性弹性接触理论确定;横向力先通过FASTSIM求解，然后再采用FASTSIM-A理论对蠕滑力作非线性修正。

图1 轨道动力学模型

1.4 轨距不平顺仿真计算

轨距不平顺有对称外凸、对称内凹、单边外凸和单边内凹四种基本形式，见图2。分别建立了以上4种轨距不平顺形式，线路条件分别为直线和曲线。曲线半径采用设计速度为250 km/h和350 km/h最不利的情况，其中速度250 km/h半径为2800 m，速度350 km/h半径为5500 m。工况中轨距不平顺递变率都为1‰，具体计算参数见表1。

图2 轨距不平顺形式

轨距不平顺激扰采用目前国际上铁路通用的余弦波［1］，其函数表达式为

式中，a为不平顺幅值;l为轨距不平顺基长。

表1 轨距不平顺动力仿真计算参数

2 仿真计算动力响应输出及计算结果

为分析轨距不平顺对车辆动力响应的影响，分别输出各工况下轮轨横向力、轮轨垂向力、脱轨系数和轮重减载率，并对结果进行对比分析。

2.1 直线上列车动力响应对比分析

图3，图4给出了直线上四种轨距不平顺下的动力响应时间历程，由图可知:

图3 直线上运行速度为250 km/h列车动力响应

(1)当列车以250 km/h的速度在直线有轨距不平顺的轨道上运行时，从最大值和突变值上看，单边外凸轨距不平顺的轮轨横向力、轮轨垂向力、脱轨系数和轮重减载率最大且衰减较慢，其次为单边内凹，对称外凸和对称内凹对列车动力响应影响较小。

图4 直线上运行速度为350 km/h列车动力响应

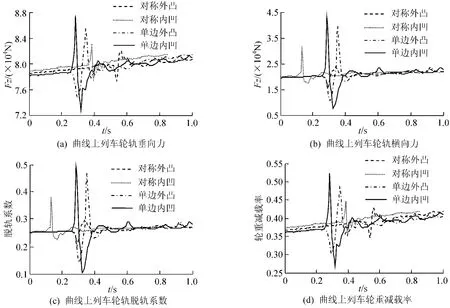
图5 曲线上运行速度为250 km/h列车动力响应

图6 曲线上运行速度为350 km/h列车动力响应

(2)当列车以350 km/h的速度在直线有轨距不平顺的轨道上运行时，从最大值和突变值上看，单边外凸轨距不平顺的轮轨横向力和脱轨系数最大且出现了二次峰值，其次为单边内凹;单边内凹的轮轨垂向力和轮重减载率最大，其次为单边外凸，对称外凸和对称内凹对列车动力响应影响较小。

2.2 曲线上列车动力响应对比分析

图5，图6给出了曲线上四种轨距不平顺下的动力响应时间历程，由图可知:

(1)当列车以250 km/h的速度在曲线有轨距不平顺的轨道上运行时，从最大值和突变值上看，单边内凹轨距不平顺的轮轨横向力、轮轨垂向力、脱轨系数和轮重减载率最大，其次为单边外凸，对称外凸和对称内凹对列车动力响应影响较小。

(2)当列车以350 km/h的速度在曲线有轨距不平顺的轨道上运行时，从最大值和突变值上看，单边内凹轨距不平顺的轮轨横向力、轮轨垂向力、脱轨系数和轮重减载率最大，其次为单边外凸，对称外凸和对称内凹对列车动力响应影响较小。

3 结论

(1)直线上列车以高中速在有轨距不平顺的轨道上运行时，单边轨距不平顺的轮轨横向力、轮轨垂向力、脱轨系数和轮重减载率影响较大，且突变也较大，对称轨距不平顺影响较小。其中，列车中速时，单边外凸的动力响应指标的最大值和突变值最大，列车高速时，单边外凸的轮轨横向力和脱轨系数的最大值和突变值最大，单边内凹的轮轨垂向力和轮重减载率的最大值和突变值最大。

(2)曲线上列车以高中速在有轨距不平顺的轨道上运行时，单边轨距不平顺的轮轨横向力、轮轨垂向力、脱轨系数和轮重减载率最大值较大，且突变值也较大，对称轨距不平顺影响较小。其中，单边内凹的动力响应指标的最大值和突变值最大。

因此，对轨道维修时应分别对直线和曲线上轨距不平顺最不利工况予以重视，以提高列车的行车安全性和舒适性。

［1］翟婉明.车辆-轨道耦合动力学［M］.北京:科学出版社，2007.

［2］王伟华.土路基双块式无砟轨道垂向动力特性分析［D］.成都:西南交通大学土木工程学院，2009.

［3］任尊松.车辆动力学基础［M］.北京:中国铁道出版社，2009.