千米级斜拉桥主梁挠度非线性随机静力分析

刘晓銮， 张杨永， 周云岗

(同济大学 桥梁工程系，上海 200092)

0 概述

随着苏通长江大桥和香港昂船洲大桥的建成通车，斜拉桥已进入千米级领域。随着斜拉桥跨径的增大，结构刚度急速下降，几何非线性效应更加突出。国内外已有学者对跨径600 m左右的斜拉桥静力可靠度做了研究［1-2］。目前对千米级斜拉桥的研究成果均是在确定性分析基础之上的［3-4］，尚未有学者对其做过考虑几何非线性的随机静力分析。

由于实际桥梁结构在材料性能、几何尺寸、作用荷载等方面存在大量不确定因素，必然导致其结构响应与确定性分析结果存在一定的差异［5］。蒙特卡罗法通过对随机变量的大量抽样和有限元分析计算结构失效概率，常用来检验其它方法的精确性。响应面法通过研究结构响应与结构各种随机因素之间的关系来构造结构响应面方程，运用响应面方程即可进一步研究千米级斜拉桥的结构随机特性。

1 响应面法

大型桥梁结构由于具有很强的非线性特征，不容易获得其极限状态方程的具体表达式，因而无法直接采用一次二阶矩法(FORM)计算其可靠指标。采用不含交叉项的二次多项式来表示响应面函数［6］

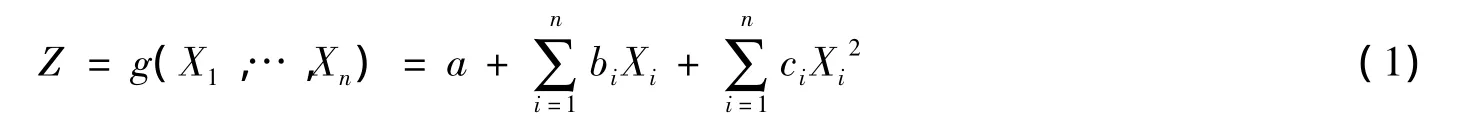
其待定系数为(2n+1)个，n为随机变量的个数。

采用以求得验算点为目的的迭代序列响应面方法，应用插值技术确定响应面待定系数，结合验算点法(JC)求解隐式极限状态方程的可靠指标。具体步骤如下:

(3)利用这2n+1个点估计值解出响应面待定因子a，bi，ci(i=1，2，…，n)，得到以二次多项式表达的近似功能函数，从而确定极限状态方程;

(4)用一次二阶矩法求解验算点XDk和可靠指标βk，其中上标k表示第k次迭代;

2 应用实例

2.1 实例简介

苏通长江大桥为带辅助墩的双塔双索面钢箱梁斜拉桥，主桥跨径布置为(100+100+300+1088+300+100+100=2088)m。桥塔为混凝土结构，由双塔柱组成倒Y形，塔高300 m。斜拉索呈扇形布置，每一扇面由34对斜拉索组成，标准索距16 m。主梁为带风嘴的闭口钢箱梁，梁高3.5 m，主梁总体宽度为35.4 m。该桥的总体布置如图1所示。

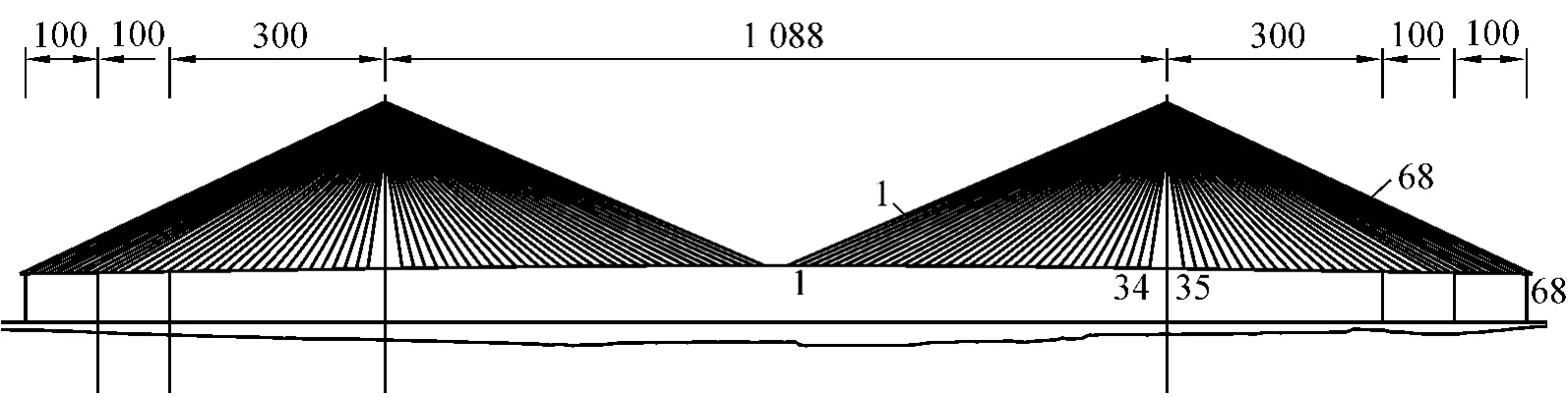
图1 苏通长江大桥总体布置图(单位:m)

2.2 有限元模型

利用ANSYS软件建立苏通长江大桥的有限元模型如图2所示。其中，主梁和桥塔采用空间梁单元，斜拉索采用空间杆单元，斜拉索和主梁通过刚臂单元连接。斜拉索垂度效应用10段杆单元模拟。

图2 苏通长江大桥空间有限元模型

2.3 主梁挠度可靠指标计算

由于目前已完成的“公路桥梁可靠度研究”课题［7］中，没有对斜拉桥梁、塔、索的材料、几何尺寸等做过专门的统计调查。参考以往学者对千米以下斜拉桥的随机静力分析成果［1-2］，假定苏通长江大桥的结构随机变量为斜拉索、桥塔和主梁的弹性模量Ei、材料密度γi和截面面积Ai，桥塔和主梁的截面惯性矩Ii和汽车活荷载q，其统计特征如表1所示。在正常使用极限状态下，根据《公路斜拉桥设计规范》(JTJ 027—96)，主梁在汽车荷载(不计冲击力)作用下允许的最大竖向挠度［u］=L/400=2.72 m(L为中跨跨径)，建立极限状态方程

式中，uv为主梁最大挠度，按照响应面法，可以表示为Ei、γi、Ai、Ii及q等随机变量的函数。

采用响应面法模拟公式(2)，求解主梁最大挠度可靠指标，并与蒙特卡罗法模拟结果对比，如表2所示。蒙特卡罗法模拟次数为1000次，相对误差计算公式为|(本文结果－蒙特卡罗法结果)/蒙特卡罗法结果|×100%。

从表2可以看出，响应面法可靠指标计算结果与蒙特卡罗法模拟结果吻合得很好。文献［7］认为正常使用极限状态的目标可靠指标βT宜限在0.675～1.645之间，由此可见，苏通长江大桥主梁最大挠度满足此目标可靠指标要求。

表1 苏通长江大桥随机输入变量的统计特征

表2 可靠指标计算结果对比

2.4 可靠指标敏感因素分析

可靠指标对随机变量平均值和标准差的敏感度，具体计算公式为［8］

式中，β是可靠指标，αi是第i个随机变量的方向余弦，μi和σi分别是第i个随机变量的平均值和标准差。

计算结果发现，主梁最大挠度可靠指标β对斜拉索弹性模量E1的平均值和标准差的敏感程度最高，分别为0.8926和 －0.8976，其次是主梁截面面积 A19(－0.3415和 －0.1314)和汽车活荷载 q(－0.1824和－0.0375)，对其它随机变量平均值和标准差的敏感程度很低。其中，截面面积为A19的主梁在中跨跨中段总长度为400 m。敏感度为正值表示可靠指标与随机变量的平均值或标准差成正比，敏感度为负值表示可靠指标与随机变量的平均值或标准差成反比。因此，苏通长江大桥主梁挠度可靠指标与斜拉索弹性模量E1的平均值成正比，与E1的标准差成反比，与主梁截面面积A19和汽车活荷载q的平均值和标准差成反比。

2.5 随机变量变异对主梁挠度的影响分析

利用响应面拟合方程对各随机变量变异时的主梁挠度响应进行分析，结果如图3所示。从图中可以看出，苏通长江大桥主梁挠度随斜拉索、主梁和桥塔弹性模量的增加而减小，斜拉索弹性模量的变化对主梁挠度的影响程度比主梁弹性模量的变化显著。桥塔弹性模量的变化对主梁挠度影响很小。斜拉桥主梁挠度随斜拉索截面面积(A1、A2、A3和A4)的增大而减小，这是因为当斜拉索截面面积增大时，结构刚度增大，主梁挠度随之减小。苏通长江大桥主梁挠度随汽车活荷载q的增大而增大。

图3 随机变量变异时主梁最大挠度的变化规律

主梁截面面积A19的变化对苏通长江大桥主梁挠度的影响较大，主梁挠度随主梁截面面积的增大而增大。文献［2］对南京长江二桥(主跨628 m)进行随机静力分析时，发现主梁挠度随主梁截面面积的增大先减小后增大，原因是主梁的自重和刚度对挠度都有影响，但是影响程度不同。当主梁截面面积较小的时候，主梁刚度对挠度的影响比自重显著，因此主梁挠度随主梁截面面积的增加而减小;当主梁面积增大到一定程度后，主梁自重对挠度的影响比刚度显著，因此主梁挠度随主梁截面面积的增加而增加。分析的苏通长江大桥主跨跨径为1088 m，主梁挠度随着主梁截面面积的增大而增大，没有出现下降段，说明主梁自重对挠度的影响始终比刚度显著，也从侧面说明了千米级斜拉桥的结构刚度下降，结构的柔性更大。

3 结论

采用不含交叉项的二次多项式的响应面法求解千米级斜拉桥的可靠指标与蒙特卡罗法模拟结果吻合得很好，可以用于千米级斜拉桥的非线性随机静力分析。

通过对苏通长江大桥的非线性随机静力分析可知:斜拉索弹性模量的变异对千米级斜拉桥主梁挠度的影响最为显著，斜拉索弹性模量的变异比主梁弹性模量的变异对主梁挠度的影响显著，桥塔弹性模量的变异对主梁挠度的影响很小。千米级斜拉桥主梁挠度随斜拉索截面面积的增大而减小，随主梁截面面积的增大而增大，主梁自重对挠度的影响始终比主梁刚度显著。

［1］程进，肖汝诚.斜拉桥结构静力可靠度分析［J］.同济大学学报:自然科学版，2004，32(12):1593-1598.

［2］陈铁冰，谭也平.基于神经网络的斜拉桥非线性随机静力分析［J］.重庆建筑大学学报，2006，28(4):42-46.

［3］张建民，肖汝诚.千米级斜拉桥施工过程中的索力优化与线形控制研究［J］.土木工程学报，2005，38(7):54-60.

［4］唐政，石雪飞，应天益.千米级斜拉桥汽车荷载作用下非线性静力响应研究［J］.石家庄铁道学院学报，2009，22(4):12-17.

［5］李生勇，张哲.自锚式悬索桥主梁挠度非线性随机静力分析［J］.武汉理工大学学报，2010，34(2):266-269.

［6］Bucher C G，Bourgund U.A fast and efficient response surface approach for structural reliability problems［J］.Structural Safety，1990，7(1):57-66.

［7］李扬海，鲍卫刚，郭修武，等.公路桥梁结构可靠度与概率极限状态设计［M］.北京:人民交通出版社，1997.

［8］Hohenbichler M，Rackwitz R.Sensitivity and importance measures in structural reliability［J］.Civil engineering systems，1986(3):203-210.