基于非线性最小二乘的坐标转换及精度分析
2011-04-27尹慧芳党亚民郑作亚
尹慧芳,党亚民,郑作亚,3
(1.中国测绘科学研究院大地测量与地球动力学研究所,北京100830;
2.山东科技大学测绘科学与工程学院,山东青岛266510;3.海岛(礁)测绘技术国家测绘局重点实验室,山东 青岛266510)
0 引 言
GPS测量所用的坐标系是WGS-84坐标系,实际应用中需要将WGS-84转换为国家大地坐标系坐标或地方坐标系坐标,这就要进行坐标系之间的转换。坐标系转换方法主要有数值变化方法、基于坐标平移量的转换方法以及基于数学模型的转换。目前常用的是基于数学模型的转换—七参数转换方法。七参数转换具有理论依据强、精度高且适用于大范围数据的坐标转换等优点。
三维坐标转换的七参数线性模型对于旋转角较小时,能满足一般的精度要求,且计算过程简单,但当旋转角较大时就会存在较大的模型误差,严重影响坐标转换结果的准确性,无法适用。对于大旋转角的坐标转换问题,文献[1]和文献[2]分别提出了三维直角坐标转换的非线性方法,有效减小模型误差对坐标转换结果的影响,但这些方法都是基于近似的正交性条件方程进行求解,结果不会很精确。基于非线性最小二乘平差原理[3]求解坐标转换参数,在最小二乘原理的前提下,寻求满足精确正交性条件方程的解,基本可以消除线性化模型误差的影响,获得坐标转换七参数的精确解。通过模拟算例可以看出非线性最小二乘方法在七参数的求解精度方面具有一定优势。
1 迭代求解
三维坐标转换七参数模型为



其中:

若已知三个公共点,即可按照最小二乘原则进行平差计算,求得七参数的值。计算时,将求得的转换参数作为初值重复进行线性化和最小二乘平差的过程,直至满足某一设定条件。
2 非线性最小二乘
设七参数模型误差方程式为[5]
如长江干流安徽无为大堤惠生堤段,堤基为沙基,地面覆盖土层薄,汛期高水位时容易形成渗透破坏。1998年、1999年长江大水,安徽长江同马大堤有的堤段堤后二三百米处都出现翻沙鼓水险情,为了保证堤防的安全,对很多堤段都采取加做黏土铺盖、堤脚填塘、堤后盖重、增做戗台等措施进行加固处理。如果在上述范围内种树,树根穿透覆盖层,汛期易形成管涌险情。

根据最小二乘原理,所求的最小二乘解应满足:
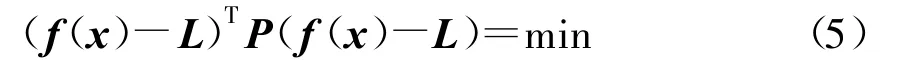
即满足非线性方程组[3]

满足式(6)的解即为式(4)的最小二乘解。将式(6)在近似值x0处泰勒级数展开,取至一次项得
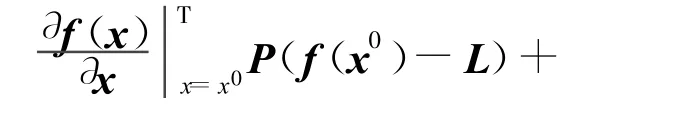

W为n×t×t的立体阵;n为观测方程个数;t为必要观测数。
则上式可表示为

上式中的[][]表示立体阵的方括号乘法。解式(8)可得:

则:

将˜x再作为初值x0进行迭代计算,直至δx的一范数值小于某一确定的阈值为止,即可得最小二乘法则下的最优解。
该算法是在最小二乘原则的前提下,寻求满足精确正交性条件方程的七参数解,而迭代的非线性参数平差方法只是满足近似的正交性条件方程。因此,本文的求解精度会有一定的提高。
3 模拟算例
借鉴文献[6]中的模拟数据产生方法,先将8个点的旧坐标数据(见表1)沿X、Y、Z各平移200 m,400 m、600 m,再分别绕坐标轴逆时针旋转10°、20°、30°,尺度参数假定为1,通过FORTRAN编程得到坐标转换后旧坐标数据在新坐标系下的坐标值(见表1)。

表1 模拟数据
根据文献[7]中对公共点选取的结论,采用分布均匀的1、3、8作为已知公共点求解七参数,求解时七参数初值设置如下:

分别采用第一部分介绍的迭代法和第二部分介绍的非线性最小二乘两种方法进行七参数的解算,通过FORT RAN语言编写程序求解7个转换参数,所得结果见表2。将非线性最小二乘求解的七参数结果带入式(1)进行旧坐标数据的坐标转换,所得的新坐标结果及其与模拟坐标真值的差值见表3。

表2 七参数计算结果

表3 非线性最小二乘求解的新坐标及与模拟真值的差值
由表2可见:非线性最小二乘方法通过求解精确的正交性条件方程得到的坐标转换参数值与真实值完全相符,与迭代求解方法相比精度有所提高(对于坐标平移参数精度约提高6×10-6m,旋转角的精度平均提高10-6°)。
算例中采用的迭代初值为
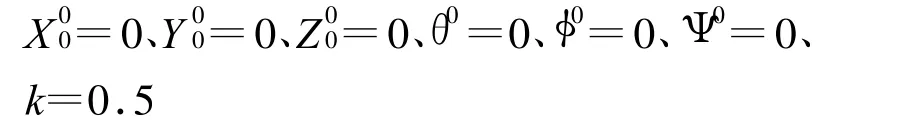
说明该方法对于初值依赖性比较小,即使初值与真值存在较大的偏差时该算法仍可以收敛到精确的最小二乘解。
由表3的坐标转换结果可见:该方法在进行大旋转角的三维直角坐标转换时,坐标转换结果与理论真实值完全相符,证明该方法求解结果精确可靠,对于解决大旋转角的坐标转换问题具有重要意义。
4 结 论
七参数线性模型仅适用于旋转角较小的空间坐标转换,当旋转角较大时无法适用。求解非线性方程组的经典方法是迭代解法,即首先将模型进行线性化,然后采用迭代法进行求解,由于该方法求解时只是寻求满足近似正交性方程的解,因此,只能满足一般精度要求的坐标转换问题。非线性最小二乘法是在最小二乘的前提下寻求满足精确正交性条件方程的七参数解,根据式(7)可以看出该方法顾及到了线性化过程中的二次项,因此,该方法理论上会比迭代法求解非线性问题具有更好的精度。通过模拟算例的分析结果可知:该算法对初值的依赖比较小;能够精确解决大旋转角的三维直角坐标转换问题,克服了传统七参数线性模型在解决大旋转角坐标转换问题中的缺陷;通过与迭代法进行对比,可以看出该算法求解坐标转换参数精度略有提高。
[1] 罗长林,张正录,邓 勇,等.基于改进的高斯-牛顿法的非线性三维直角坐标转换方法的研究[J].大地测量与地球动力学,2007,27(1):50-54.
[2] 曾文宪,陶本藻.三维坐标转换的非线性模型[J].武汉大学学报◦信息科学版,2003,28(5):566-568.
[3] 刘国林,姜 岩,陶华学.非线性最小二乘平差[J].测绘学报,1998,27(3):224-230.
[4] 党亚民,成英燕,薛树强.大地坐标系统及其应用[M].北京:测绘出版社,2010.
[5] 武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M].武汉:武汉大学出版社,2003.
[6] 陈 宇,白征东.基于非线性最小二乘算法的空间坐标转换[J].大地测量与地球动力学,2010,30(2):129-132.
[7] 王玉成,胡伍生.坐标转换中公共点选取对于转换精度的影响[J].现代测绘,2008,31(5):13-15.
