GNSS卫星三种站心极坐标的关系*
2011-04-27刘长建黄献波吴洪举
刘长建,黄献波,吴洪举
(1.信息工程大学测绘学院,河南 郑州450052;2.河南财经政法大学基建处,河南 郑州450052)
0 引 言
全球导航卫星系统(GNSS)的应用中,有一类坐标系常用于描述GNSS卫星与测站的相对位置关系,称为站心坐标系[1-2],有时也称为站心地平坐标系[3],可具体再分为站心直角坐标系和站心极坐标系,二者一一对应,很容易相互转换,但前者常被用作求取后者的过渡。
站心直角坐标系通常取左手坐标系。有三种常用的站心直角坐标系,根本区别在于z轴指向不同,分别为测站参考椭球面外法线方向、测站铅垂线上方向、测站地心向径方向(相应的站心极坐标系后文简称为站心极坐标系1、站心极坐标系2、站心极坐标系3)。鉴于三种站心直角坐标系关系简单,且实用中又经常使用站心极坐标系,故本文主要讨论三种站心极坐标系的关系。
传统大地测量中关于站心极坐标系1和站心极坐标系2的关系是在高度角很小的情况下给出的近似公式[4-5],不再适用于GNSS卫星,其关系式需要重新给出。此外,对于三种站心极坐标的误用或近似代替情况,其差别如何,也是一个值得探讨的问题。
1 站心极坐标系1(A1,z1,ρ1)
站心极坐标系一般都有相应的站心直角坐标系与之对应,为便于理解,可先从后者开始。如图1所示,原点位于测站i,z轴与测站椭球面法线重合,指向天顶方向,x轴位于测站大地子午面内,指向北极方向,y轴与x轴、z轴构成左手系。相应该直角坐标系的站心极坐标系可用(A1,z1,ρ1)表示,它们原点相同,其中,卫星j的方位角A1由 x轴正向顺时针量取,范围[0°~360°],天顶距由z轴正向向下量取,范围[0°~180°],极距ρ1为测站i至卫星j的距离。
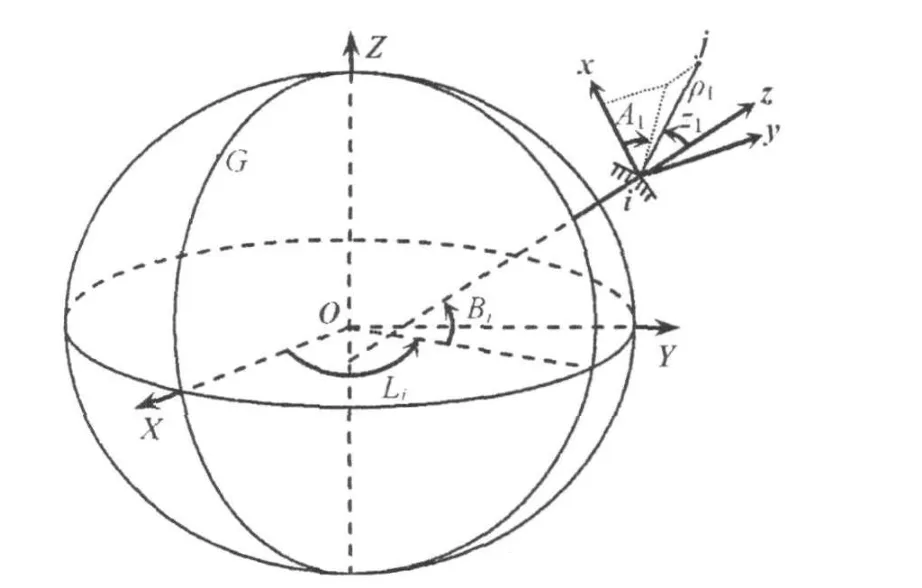
图1 站心极坐标系
很多文献中已给出卫星j在i-xyz坐标系的直角坐标,即

或

卫星j的站心极坐标(A1,z1,ρ1)为

2 站心极坐标系2(A2,z2,ρ2)
如果将图1中的z轴取为测站铅垂线上方向,x轴位于测站天文子午面内,y轴仍与x轴、z轴构成左手系,则可得到站心直角坐标系2。这种坐标系具有明显的实际意义,因为仪器垂直轴一般都要求与测站铅垂线重合。相应的站心极坐标系可用(A2,z2,ρ2)表示,其量取方法和范围同站心极坐标系1。
可仿照文献中的推导,卫星在站心直角坐标系2中的坐标为
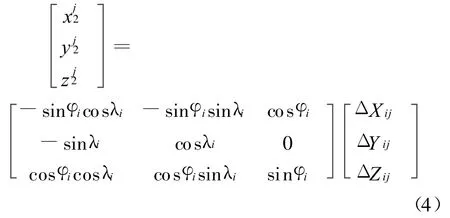
或

式(4)、(5)中:φi、λi为测站的天文纬度和经度;为卫星在站心直角坐标系 2下的坐标向量;ΔXij仍为地心直角坐标系O-XYZ下测站至卫星的向量;M2为正交变换矩阵。
卫星j的站心极坐标(A2,z2,ρ2)为
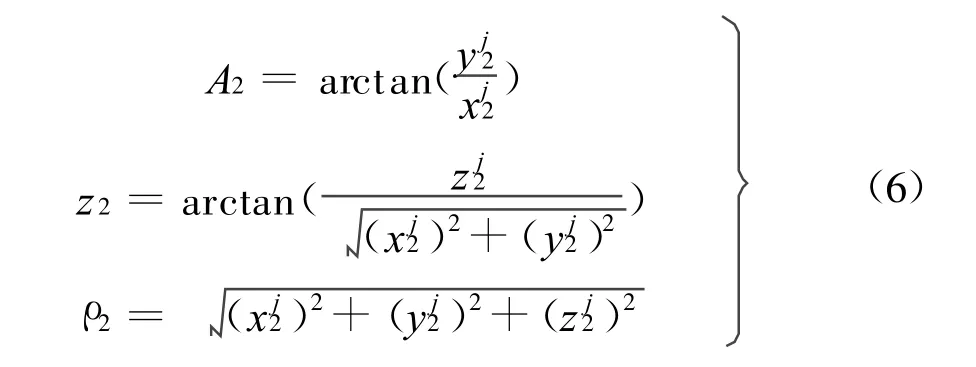
3 站心极坐标系3(A3,z3,ρ3)
如果将图1中的z轴取为地心至测站的向径方向,x轴位于测站大地子午面内,y轴与x轴、z轴构成左手系,则可得到站心直角坐标系3。相应的站心极坐标系3可用(A3,z3,ρ3)表示,它常用于求取单层电离层穿刺点的坐标,量取方法和范围也同站心极坐标系1。
类似地,卫星在站心直角坐标系3中的坐标为

或

式(7)、(8)中:φi、Li为测站的球心纬度和大地经度为卫星在站心直角坐标系3下的坐标向量;ΔXij仍为地心直角坐标系O-XYZ下测站至卫星的向量;M3为正交变换矩阵。
卫星j的站心极坐标(A3,z3,ρ3)为

4 GNSS卫星三种站心极坐标的关系
由于M1、M2、M3为正交矩阵,对(2)、(5)、(8)三式分别取模,易得 ρ1=ρ2=ρ3;Ai(i=1,2,3)之间的关系及zi(i=1,2,3)之间的关系可由图2推出。图2为站心单位球示意图:J点为卫星j的球面投影;Z1、Z2、Z3分别为测站椭球面外法线方向、铅垂线上方向、地心向径方向与球面的交点;P为平移后的地轴北极方向与球面的交点;大圆弧PG为平移后的起始大地子午面或起始天文子午面与球面的交线;u为测站几何垂线偏差,一般约十几秒[5],θ为其方向;u1为大地纬度与地心纬度之差,最大约11.8′[4]。下面以 A1、z1为参考,先讨论A2、z2与它们的关系,然后再讨论A3、z3与它们的关系。
当观测目标的高度角很小时,如小于5°,传统大地测量中通过一些近似,显式地给出了 A1、A2和z1、z2的差值公式,但对于空间卫星,这一前提显然失效,因此,只能隐式地给出这一差值或通过分析给出差值的变化范围。根据球面三角形有关公式,由图2可得
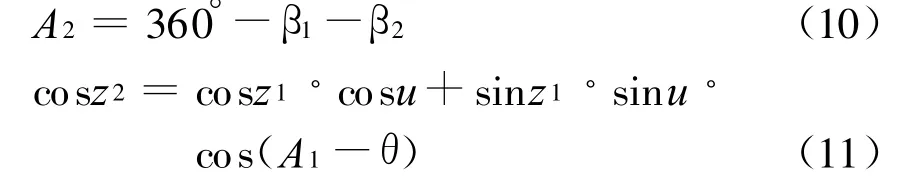
其中:

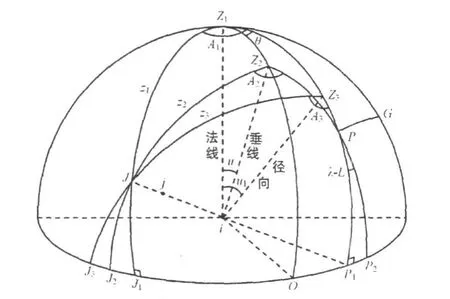
图2 站心单位球
β1为球面角Z1Z2P,对具体的测站为固定值,β2为球面角Z1Z2J,随 A1、z1变化而变化,故一般情况下,A2为 A1、z1的非线性函数,z2同理。结合以上诸式及图2,可分析一些特殊情况下它们差值的规律:
1)对于A1、A2,卫星位于Z1、Z2时,A1、A2无意义;当A1为 θ或 θ+180°时,β2为0°或180°,A2、A1之差为常数;当z1、z2相等时,A2、A1之差为A1的线性函数;当卫星位于极点(北极或南极)时,二者相等,为0°或180°;当卫星由Z1Z2P区域趋于北极P时,A2、A1之差趋于360°;当卫星由P1P2P区域趋于北极P时,A2、A1之差趋于-360°。
2)对于z1、z2,利用球面三角形大角对大边、大边对大角的性质,可以证明二者之差的绝对值在[0,u]内;当A1为θ或θ+180°时且卫星不在弧段z1z2内及其球对称的弧段内时(不含端点),二者之差的绝对值为u;当z1、z2相等时,即卫星位于过弧段z1z2中点且与该圆弧正交的大圆弧上时,二者之差的绝对值为0。
以上是A2、z2与A1、z1的关系分析,将θ取为0,u取为u1,φ取为 φ时,类似地可以得出 A3、z3与A1、z1的关系;此外,A2、z2与 A3、z3的关系也可由上述讨论类似得出。
表1给出了由导航星历算出的北半球某中纬度站全天所有GPS卫星极坐标2与极坐标1的差值统计情况,表2为极坐标3与极坐标1的差值统计情况,计算中,假定该站的u=15",θ=20°,算出的B-φ=11′20.0559″。

表1 极坐标2与极坐标1差值统计情况
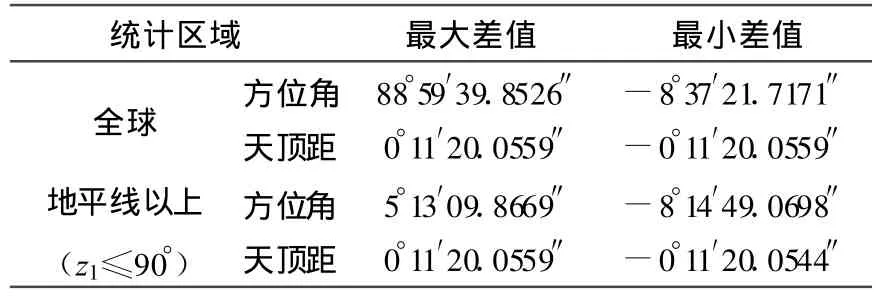
表2 极坐标3与极坐标1差值统计情况
需说明的是,由于GPS星座及按30″采样间隔进行统计的原因,表1、表2并没有反映所有可能的差值情况,但可以看出,方位角有时相差很大,最大达到了几十度。可以将A1、z1作为自变量,进一步细分间隔,按式(10)、(11)进行模拟计算统计,由于其规律和上述分析一致,这里不再列出。
5 结 论
GNSS卫星三种站心极坐标的关系中,它们的极距均相等;极坐标2的天顶距与极坐标1的天顶距之差最大不超过测站的几何垂线偏差,极坐标3的天顶距与极坐标1的天顶距之差最大不超过测站的大地纬度与球心纬度之差;它们的方位角之差变化比较复杂,最大差值接近±360°。在使用GNSS卫星不同站心极坐标时,或做某些近似时,尤其应注意方位角的差异。
[1] 周忠谟,易杰军,周 琪.GPS卫星测量原理与应用[M].北京:测绘出版社,2004.
[2] 李征航,黄劲松.GPS测量与数据处理[M].湖北:武汉大学出版社,2005.
[3] Xu Guo-chang.GPS theory,algorithms and applications[M].Springer,2007.
[4] 熊 介.椭球大地测量学[M].北京:解放军出版社,1988.
[5] 吕志平,张建军,乔书波.大地测量学基础[M].北京:解放军出版社,2005.
