基于电压灵敏度的模拟电路节点选择策略

周龙甫， 师奕兵， 赵福胜， 赵 光， 唐 红

（1.解放军第452医院，四川 成都 610061；2.电子科技大学自动化学院，四川 成都 611731）

0 引 言

随着电子产业的飞速发展，模拟电路故障诊断日益重要。在业界，电路故障诊断上的花费已经达到总成本的30%以上，而且其中对模拟电路故障进行诊断的费用占到总费用的95%。因此，对模拟电路故障诊断的研究也已经成为世界范围内的热点。经过长期的努力，在该领域已取得了一系列成果[1-11]。在工程实践中，总希望从所得到的电路信息中获取电路的内部信息。电路中的测试节点就是电路测试人员获取电路信息的入口。因此，如何合理选取电路测试节点是模拟电路故障诊断工作中非常重要的环节，同时也是模拟电路故障诊断研究领域的热点问题之一。文献[3]提出了很多查找最优测点集的算法；文献[4]中用连续二次方程的方法来产生测点集；文献[5]将模糊集概念引入到模拟电路故障诊断工作中；文献[6]采用故障隔离度和条件隔离度来描述节点的故障区分能力，并且按照每个节点的区分能力强弱来进行节点选择；文献[7]提出了一种启发式图搜索的最小测点集选择方法，将测点选择过程转化为图节点扩展过程。

该文从节点电压灵敏度定义入手，借鉴模糊组划分理论，提出故障诊断能力指标的概念，在此基础上给出一种简洁、方便可行的测试节点优选方法。

1 节点选择策略

1.1 节点电压灵敏度定义

电路节点电压灵敏度是指电路元件参数偏离其标称值时，引起的电路上测试节点电压等电路参数的变化情况，是衡量电路性能的重要参数之一。在模拟电路故障领域，基于电路灵敏度分析进行故障诊断已经是重要分支之一。

节点电压灵敏度定义[8]：当第i个元件参数Yi只有一个较小的偏移量，即Yi→0时，节点j的节点电压ej对元件参数Yi的偏导数，记为

1.2 测试节点选择的基本准则

对于一个待诊断的模拟电路而言，电路中会有多个节点。但是，并不是每一个节点上的电压值都可以方便地测量出。而且对于电路故障诊断而言，电路中出现的某些故障可能在某2个或2个以上的测试节点上体现出相同的电压信息，也就是说电路中的可测节点中会有一部分点属于冗余点。在模拟电路故障诊断中，无论以何种故障特征为依据进行故障诊断，非冗余测点的数量越多，诊断的结果就越准确；然而，测点的增加，意味着测量成本的增加和计算量的增大。因此，在模拟电路的所有可测节点中合理选择测点是模拟电路故障中的一个重要问题。

在节点选择过程中，必须遵循两项重要的法则[9]：（1）选到的测试节点个数必须满足故障诊断的需求；（2）在选择的测试节点集中尽量没有冗余节点。

1.3 测试节点上电路故障集模糊子集划分

对于n个器件，m个可测节点的模拟电路，按照式（1）定义的电压节点灵敏度计算公式可以得到每个可测节点对于每个电路器件的灵敏度指标。所有测试节点对每个电路元器件的灵敏度值可以一起构成一个 m×n维的灵敏度矩阵 Am×n。

对某个节点而言，如果电路中两个元件对该测试节点的灵敏度值差别很大（例如，两者之间相差一个数量级），那么，显然当这两个元件参数的漂移量相当时，在该可测节点上带来的电压漂移值也会有很大差别。但是，如果电路中两个元件对该测试节点的灵敏度值差别很小，这两个元件上相近的参数漂移量在该可测节点上带来的电压漂移值差别也很小，有时两者之间的差别小到无法分辨。对于后者而言，显然在该测试节点上，这两个元件上的故障是无法判别的。

文中首先按照可测节点对电路元件的灵敏度值的大小划分电路故障集模糊子集[12]。例如，对可测节点j，如果电路中元件i和元件k对节点j的电压灵敏度值在同一个数量级上，在这两个电路元件上的故障Fi和Fk就被定义为在同一个模糊子集中。与此同时，在矩阵Am×n中列向量线性相关的元件也必须定义为在同一个模糊子集中。那么对待诊断的电路而言，故障集中必然会有多个模糊子集，每个待诊断故障必然会被划分到其中一个模糊子集中；因此，模糊子集的划分是唯一的。相应地，电路的可测性与电路故障集中的模糊子集的个数成正比，即故障集中模糊子集个数越多，每个模糊子集中包含的故障越少，电路中的故障越容易相互隔离，电路的可测性越好，反之亦然。

1.4 可测节点的“选入”准则及步骤

在上述模糊子集划分的基础上，进一步寻找最佳节点集。首先介绍两个定义[9]：

NAj为某个可测节点对应的模糊子集数量；

Max（NFj）为一个模糊子集中包含的故障个数。

在测试节点选择过程中，如果一个节点具有较好的诊断能力，那么它必然应该首先被选入进测试节点集。这样一个选择过程就构成了一个可测节点的“选入”过程。对于每个可测节点，电路故障集模糊子集包含了电路故障诊断中诸多信息，就可以从这些信息中得到每个可测节点的故障诊断能力。在此，在电路的每个可测节点上定义一个新参数：故障诊断能力指标IsF（isolation of faults），计算方法如式（2）所示

显然，式（2）表明，对于某个可测节点，当没有模糊子集存在时，该节点具有最大的IsF值，等于电路中故障个数；当电路中所有故障在一个模糊子集中时，该节点的IsF值最小，等于电路中故障个数总数的倒数。

从上述模糊集划分及可测节点的选入准则，从电路所有节点中选择出可以反映电路内部信息，且最大限度地减少冗余节点的节点选择步骤可分为如下4步：

（1）对于每一个可测节点j，计算NAj和Max（NFj）；

（2）计算每一个可测节点的故障诊断能力指标IsF；

（3）选择具有最大IsF值的可测节点k。当出现多个可测节点具有相同IsF值时，在这些可测节点中任意选择其一。然后，将所有这些具有相同IsF值的可测节点全部排除出备选可测节点集合；

（4）检查所选出的可测节点是否能够有效隔离电路中所有故障，如果可以，测试节点选择过程结束；否则，跳往（3）。

2 非线性直流电路单软故障诊断实例

诊断电路为图1所示的非线性直流电路[10]。电路中各元器件的标称值为：R1=100 kΩ，R2=27 kΩ，R3=100 Ω，R4=680 Ω，R5=10 kΩ，R6=22 kΩ，R7=10 kΩ，R8=4.8kΩ，R9=1kΩ，R10=10Ω。假设容差范围为10%。

图1 非线性直流电路

2.1 测试节点选择

该电路的节点 1，2，5，6，8～10 均为可测节点，而且在以往文献中也都选择上述节点作为电路的测试节点。这种经验性的选择往往缺乏理论依据，而且使用了电路中所有的可测节点，存在着测试节点过多的问题。图2给出了按照灵敏度分析结果得到的各可测节点上故障模糊子集示意图。表1给出了图1所示电路上各可测节点IsF值。

图2 图1电路中各可测节点上故障模糊子集示意图

表1 图1所示电路上各测节点IsF值

按照节点选择步骤，由于节点2和节点6拥有最大的IsF值，首先选出节点2。节点2上还有2个模糊子集（F1，F2）和（F3，F5）。接下来必须选择可以将这 2 个模糊子集中的故障类型进行隔离的节点。按照测试节点选择策略，节点5和节点3依次被选出。这3个节点上的故障交集为

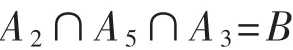
式中B表示电路的故障集，而且在B所代表的故障集中每个故障子集中仅有一个电路的故障状态。因此，可以由测试节点集{节点2，节点5，节点3}来诊断电路中所有单故障状态。

2.2 故障状态设置

给图1所示电路设置了3种故障状态，然后使用文献[12]中介绍的数学规划方法建立诊断方程来对设置的各种故障状态进行诊断。

故障状态1（容差下无故障）：电路中各元件参数取值为 R1=101 kΩ，R2=27.5 kΩ，R3=100 Ω，R4=690 Ω，R5=9.9kΩ，R6=21.8kΩ，R7=10.1kΩ，R8=4.75kΩ，R9=1kΩ，所有电路元件参数均在容差范围内。

故障状态2（无容差下单故障）：电路中R4发生故障（R4=810Ω），其余各元件参数取其标称值。

故障状态3（容差下单故障）：电路中R5发生故障（R5=11.5 kΩ），其余各元件参数均在容差范围内取值R1=100.1kΩ，R2=27.5kΩ，R3=100Ω，R4=690Ω，R6=21.8kΩ，R7=10.1kΩ，R8=4.75kΩ，R9=1kΩ。

表2给出了上述3种情况中设定的各电路元件参数的偏移量。每个元件标称值的10%（容差范围）设定为故障判断的阈值。表2中加粗的数值表示电路故障状态中故障元件相应的参数偏移量。

2.3 测试节点选择策略验证

表2 阈值及设定的电路元件参数偏移量

对于图1所示的非线性直流电路，以往的文献报道[9]中使用节点 1，2，5，6，8～10 作为测试节点对电路进行诊断的。在该文中，通过给出的选择策略，选定节点

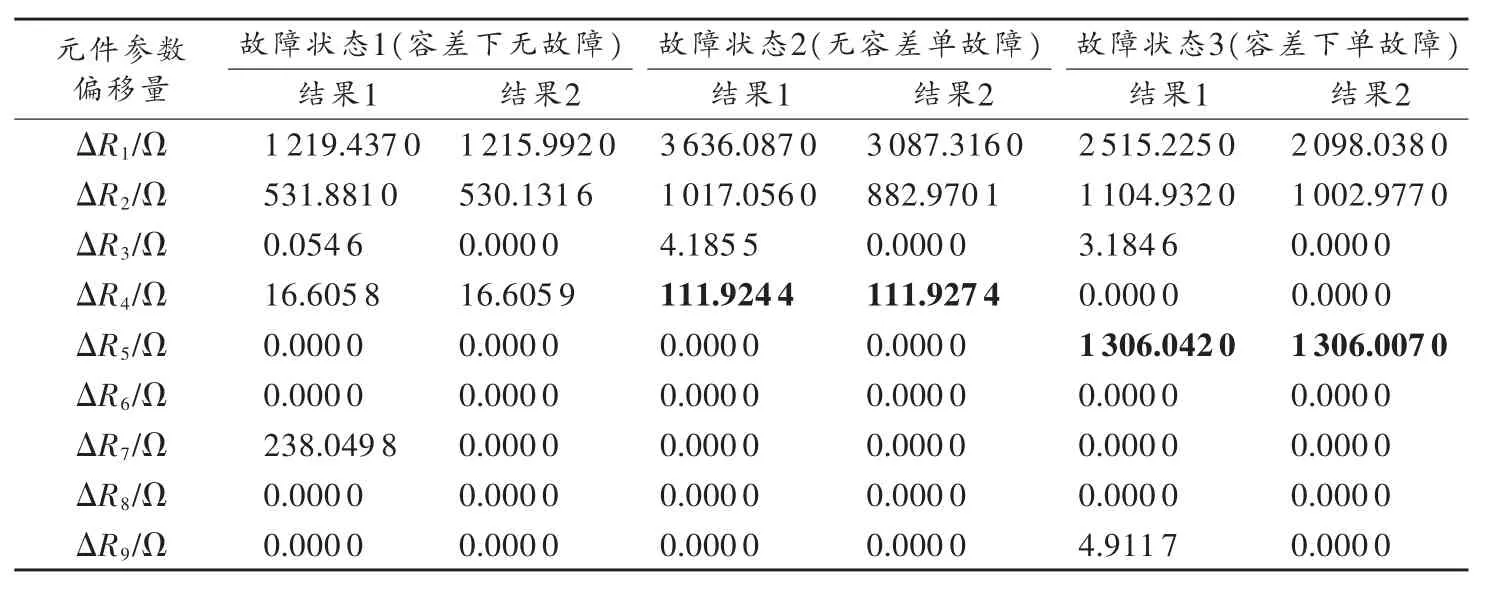
表3 使用不同测试节点对图1所示电路上3种状态诊断结果1）

2，3，5作为测试节点。为了验证测试节点数目的减少对诊断结果影响，运用MOP方法分别对不同测试节点下该电路上所设定的3种故障状态进行了诊断。诊断结果如表3所示。

需说明的是，为了给出更加详细的对比，表3中各个元件参数的单位全部选择为Ω。从表3中的诊断数值来看，不同节点选择策略所得到的诊断结果数值差别不大，尚不足以引起诊断结果的显著差别。该节中所给出的测试节点选择策略减少了测试节点的数目，使得需要建立的诊断方程减少，诊断过程得以简化。

3 结束语

该文针对模拟电路故障字典法中的测试节点选择问题进行了研究。以节点电压灵敏度为基础定义模糊组划分原则，采用所定义的故障诊断能力指标描述节点的故障区分能力，在此基础上提出了新的测试节点优选数学模型和优选算法。分析实验表明，该文提出的方法能有效地选择出可以代表电路内部信息的节点，可以有效地对电路中的故障进行诊断。

[1] Bandler J W，Salama A E.Fault diagnosis of analog circuits[J].Proceedings of the IEEE，1985，73（8）：1279-1325.

[2] Liu R W.Testing and diagnosis of analog circuits and systems[M].New York：Van Nostrand Reinhold，1991.

[3] Lin P M，Elcherif Y S.Analogue circuits fault dictionarynew approaches and imp lementation[J].Circuit Theory Appl，1985（13）：149-172.

[4]Abderrahman A，Cerny E，Kaminska B.Optimizationbased multifrequency test generati on for analog circuits[J].Journal of Electronic Testing：Theory and Applications，1996（9）：59-73.

[5] Zhou L，Shi Y，Tang J，et al.Soft fault diagnosis in analog circuit based on fuzzy and direction vector[J].Metrol Meas Syst，2009（1）：61-75.

[6] 汪鹏，杨士元.模拟电路故障诊断测试节点优选新算法[J].计算机学报，2006，29（10）：1780-1785.

[7]杨成林，田书林，龙兵，等.基于启发式图搜索的最小测点集优选新算法[J].仪器仪表学报，2008，29（12）：2497-2503.

[8] Li F，Woo P Y.The invariance of node-voltage sensitivity sequence and its application in a unified fault detection dictionary method[J].IEEE Trans，1999，46（10）：1222-1227.

[9] Prasad V C.Selection of test nodes for analog fault diagnosis in dictionary approach[J].IEEE Transaction on Instrumentation and Measurement，2000，49（6）：1289-1297.

[10]Tadeusiewicz M，Korzybski M.A method for fault diagnosis in linear electronic circuits[J].International Journal of Circuit Theory and Application，2000（28）：245-262.

[11]周龙甫，师奕兵，赵光，等.容差条件下模拟电路软故障的数学规划诊断方法[J].电子测量与仪器学报，2010，24（3）：237-243.

[12]彭祖赠，孙韫玉.模糊（Fuzzy）数学及其应用[M].2版.武汉：武汉大学出版社，2007.