基于CORDIC算法的直角坐标与球面坐标变换电路的FPGA实现

2011-04-26陈彦来

舰船电子对抗 2011年1期

陈彦来

（船舶重工集团公司723所,扬州 225001）

0 引言

在雷达数据处理信号模拟器中,目标的初始位置、速度、加速度等信息通常是以球面坐标形式给出的,而目标位置的外推需要在直角坐标系中进行,因此需要将目标初始位置、速度、加速度等信息从球面坐标系变换到直角坐标系,也就是将初始位置、速度、加速度矢量在直角坐标系中进行分解,得到其在X轴、Y轴、Z轴上的坐标,然后按照经典运动学公式进行外推；在得到目标下一时刻X、Y、Z坐标后,通常还要将其转换成相应的距离、方位角、俯仰角信息,也就是进行直角坐标系到球面坐标系的变换。现场可编程门阵列（FPGA）以其高速性和灵活性在现今的雷达数据处理领域已经得到了广泛的应用,但如果处理算法中需要计算超越函数,例如 sinθ,cosθ,arcsinx,arccosx,xn等,通常采用查表法和泰勒级数展开法。使用有限的FPGA面积设计高精度的数据表格,特别是在需要多张数据表格的情况下,其设计有一定难度。泰勒级数展开法可以将复杂的函数分解为一系列的乘方和加减法运算,解决计算精度的问题,但乘方运算需要消耗过多的FPGA硬件资源；另外还有些超越函数的泰勒级数展开式本身就不存在（例如反三角函数等）,因此泰勒级数展开法在坐标转换电路中也存在一定的局限性。有碍于FPGA器件面积消耗和计算精度、速度之间的矛盾,直角坐标与球面坐标变换电路不得不考虑其他实现方法。CORDIC算法能够方便地计算正余弦、反正余弦、乘方、开方等运算,并且在实现过程中仅用到加法器和移位器,与FPGA的特点完全吻合,能够完成直角坐标与球面坐标变换电路设计。

1 利用CORDIC算法进行坐标变换的算法原理

1.1 CORDIC算法的基本原理

CORDIC算法最初由Volder于1959年提出,其基本数学思想是通过一系列固定的、与运算基数相关的角度的不断旋转、累加而逼近所要旋转的角度。如图1所示,向量OA绕原点O逆时针旋转θ角度后到达向量OB位置,假设A点坐标为（xi,yi）,B点坐标为（xj,yj）,则:

图1 矢量旋转模型

假设向量OA逆时针旋转θ角度是由N次微旋转所构成的,由式（1）可知:向量OA的第n+1次微旋转可表示为:

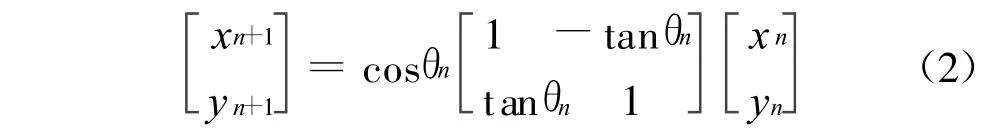
式中:n=0,1,…,N-1。

由式（1）、（2）,可得:

针对FPGA的结构特点,选取θn=arctan（1/2n）,即 tanθn=1/2n。对式（3）前面的系数K取极限得:

如果忽略常系数K,式（2）可表示为:

式中:Si={1,-1},Si=1表示第n+1微旋转方向为逆时针,Si=-1表示微旋转方向为顺时针。

根据每次微旋转方向的判定准则,CORDIC算法有旋转模式和矢量模式2种。旋转模式是以角度误差的符号作为每次微旋转方向的判断依据,最终使角度误差等于零或趋近于零,可用于求正余弦值,适用于球面坐标系到直角坐标系变换；矢量模式是以每次微旋转后旋转矢量Y轴坐标的符号作为下次微旋转方向的判断依据,最终使旋转矢量与X轴重合或趋近重合,可用于求极径和极角,适用于直角坐标系到球面坐标系变换。

1.2 CORDIC算法旋转模式计算正余弦值

假定起始向量为OA,其中A点坐标为（1,0）,经过N次微旋转后到达终止向量OB的位置,B点坐标为（x,y）。从起始向量到终止向量旋转的角度为θ,则B点坐标为（cosθ,sinθ）,也就说通过矢量旋转得到了θ角度的正余弦值。为了通过若干次的微旋转等于或逼近旋转角度θ,则需要按照式（6）的规则进行每次微旋转旋转方向的判断。式（6）中θerr_n=θ-θn。

由矢量旋转的几何关系可知:N次微旋转后的B点横坐标即为 cosθ,纵坐标即为 sinθ,也即利用CORDIC算法巧妙地解决了球面坐标系到直角坐标系变换过程中正余弦值的计算问题。

1.3 CORDIC算法矢量模式计算极径和极角

假设起始向量为OA,点A坐标为（xi,yi）,旋转终止向量为OB,点B坐标为（xj,0）。从OA到OB的旋转过程可以通过N次微旋转完成,其每次微旋转方向由式（8）、（9）决定。

若yn＞0,则:

由矢量旋转的几何关系可知:B点横坐标xj为向量OA的极径,旋转的角度θ为向量OA的极角。由于arctan（2-n）为一系列常数值,可以离线计算,因此平面直角坐标系到球面坐标系变换过程中复杂的平方、开方、反三角函数计算可以通过CORDIC算法简化为简单的移位和加减运算。

1.4 CORDIC算法实现直角坐标与球面坐标变换

如图2所示,假设任一点A的直角坐标为（x,y,z）,球面坐标为（R,α,β）,根据几何关系可知:x=Rcosβcosα,y=Rcosβsinα,z=Rsinβ；依据式（6）原则,按照CORDIC算法的旋转模式进行迭代运算 ,可以计算出 cosβ,sinα,sinβ,再进行乘法运算即可完成球面坐标到直角坐标的变换；而直角坐标到球面坐标变换分为2步进行:首先利用CORDIC算法,在XOY平面内,依据式（7）、（8）计算出OB和α；然后再次利用CORDIC算法,在ZOB平面内,依据式（7）、（8）计算出OA和β,至此完成直角坐标到球面坐标的变换。

2 基于CORDIC算法的直角坐标与球面坐标变换电路的FPGA实现

直角坐标与球面坐标变换分为直角坐标到球面坐标变换和球面坐标到直角坐标变换2种,下面以直角坐标到球面坐标变换为例来说明直角坐标与球面坐标变换电路的FPGA实现。

图2 直角坐标和球面坐标变换

2.1 CORDIC算法的级联实现

由式（8）、（9）可知,CORDIC算法的绝大部分计算为迭代运算,在FPGA中有2种实现方案。其一为设计一个有限状态机,然后利用其状态变化控制每次的迭代运算,直至完成一次坐标变换；其二为流水方式,构造若干个不同的迭代结构,对其进行流水线操作,直至计算出结果。前者需要的FPGA资源少,但进行一次变换所需时间长,并且不能进行流水线处理,不利于系统的实时算法实现；后者对FPGA的资源要求高,但平均计算时间短,在流水的情况下,可以达到系统频率,有利于系统的实时处理。在本文中采用流水线的处理方式,其单次迭代结构如图3所示。

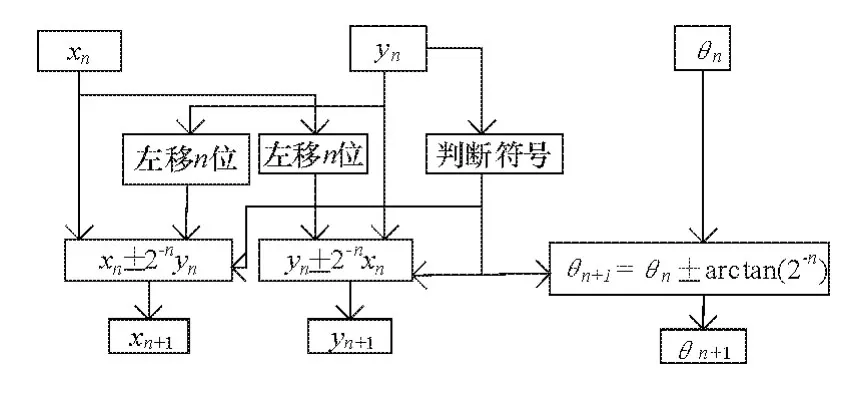
图3 CORDIC算法流水线处理单次迭代结构

2.2 CORDIC算法的预处理模块

在CORDIC算法迭代处理过程中,假设每次微旋转均为逆时针方向,且微旋转次数为无穷大,最大可旋转角度为 θmax,则 θmax≈1.743 3。为了使微旋转后的矢量落在X正半轴（或趋于X正半轴）,则被旋转的矢量极角θ应满足-θmax≤θ≤θmax；同时通过大量仿真实验发现,当被旋转矢量靠近Y轴时,极角θ的计算误差较大。

在本文中,为了使旋转矢量极角达到2π,同时减少角度计算误差,加入了CORDIC算法的预处理模块,处理原则为:

（1）如果被旋转矢量在第二象限,则通过Y轴对称将其变换到第一象限；如果被旋转矢量在第三象限,则通过原点对称将其变换到第一象限；如果被旋转矢量在第四象限,则通过X轴对称将其变换到第一象限。

（2）如果被旋转矢量变换后θ＞0.25π,则把变换后旋转矢量关于Y=X的对称矢量作为最终的旋转矢量。由于在对被旋转矢量进行微旋转前进行了对称变换,必然会影响到极角的计算结果,在CORDIC流水计算完成后需要对极角的计算结果进行修正；而对于极径而言,不会随对称变换而发生变化,因而CORDIC算法计算出的值即为其真实值。考虑原则（1）、（2）以及极角计算结果的修正,CORDIC算法预处理模块计算规则和后处理极角修正规则如表1所示。

2.3 CORDIC算法的后处理模块

利用CORDIC算法实现直角坐标到球面坐标变换的后处理模块主要是实现极角修正和极径缩放（乘以式（3）中的常数K）。其中极角的修正规律见表1的最后一列；极径缩放通过乘以一个固定的因子来实现,可以利用FPGA的DSP IP核来实现,在此不再论述。

2.4 直角坐标到球面坐标变换电路的FPGA实现

根据前面所述,直角坐标到球面坐标变换分为两部分:其一为在XOY平面利用CORDIC算法计算OB和 α；其二为在ZOB平面内,再次利用CORDIC算法计算OA和β,其FPGA电路模块划分如图4所示。

图4 直角坐标到球面坐标变换电路的FPGA实现模块划分

其中x0、y0为原始矢量的直角坐标,x1、y1为进行坐标对称变换后的直角坐标,θ17为CORDIC算法计算出的极角,θ为其修正值。

在图4中,clk为时钟信号,xyz_inen为输入使能信号,qiumianzuobiao_outen为输出使能信号,xin、yin、zin 为直角坐标输入 ,jijing、fangweijiao、yangjiao为球面坐标输出。inst1完成直角坐标输入信号的锁存,inst2完成在XOY平面的变换,inst6完成ZOB平面的变换；inst4形成输出使能信号,inst3,inst5完成数据同步。

3 试验结果

本文利用Altera公司的QuartusⅡ7.2软件,采用VHDL硬件描述语言对直角坐标到球面坐标变换电路模块进行了功能描述和时序仿真,待仿真结果正确后综合出电路网表,最后下载到Altera公司生产的StratixⅡ器件EP2S90F1020I4中进行了试验验证。图5为时序仿真波形,其中系统时钟clk为40 MHz；xin为xin_0=-500,每个时钟周期增加100的等差数列；yin为yin_0=200,每个时钟周期递减50的等差数列；zin为zin_0=50,每个时钟周期增加10的等差数列。