农业科学研究中正交试验选优分析的新方法

徐向宏

(甘肃农业大学生命科学技术学院,甘肃 兰州 730070)

正交试验是使用正交表来安排多因素多水平试验的一种试验方法。由于正交表能够保证因素各水平条件均衡，进而可比较各水平的试验指标的差异选优[1-6]，大量地节省试验次数。但在多因素、多水平的正交试验中，如果因素间有交互作用，正交试验设计中未知参数的个数(m)将呈指数增长，试验次数将大量增加(n>m)。例如，5个因素，每个因素有5个水平的正交设计有182未知参数[7]。鉴于此，正交试验设计特别强调使用2水平或3水平的正交表，但2水平或水平数少的设计不能全面给出正确的或充分的信息[7]，会影响统计结论的准确性。

提高正交试验统计结论的准确性是农业科学统计研究的重要内容，增加试验次数既增加试验成本，又增加能耗，在实际研究案例中应用相对有限。因而，原正交试验选优分析方法存在的缺陷仍然成为影响统计结论正确性的关键因素：首先，在正交试验设计中，因素的水平被设定，因而对其试验结果的优选分析被限制；其次，在各因素间交互作用存在的情况下，正交试验设计的选优分析有可能出现较大偏差。因此，如何既不增加试验次数、减少未知参数数目，又能从混杂现象中揭示出响应与因素间的关系，提高正交试验设计优选方法的正确性，对农业科学研究中精确统计分析具有重要意义。

本研究以非数量与数量混杂的多因素、多水平正交试验为例，采用高次多项式回归模型对重复正交试验进行优选分析，以期解决因素间可能存在的交互作用及固定水平限制可能对选优的干扰。

1 研究方法

1.1数据来源 数据来源于文献[4]，其研究内容为各种药剂种类、浓度和剂量及其不同水平对花生(Arachishypogaea)锈病防治效果的影响。为探讨花生锈病药剂防治效果的好坏，进行了药剂种类(A)、浓度(B)、剂量(C)3因素试验，各有3个水平，选用正交表L9(34)进行随机区组试验设计，2次重复，小区面积133.3 m2，设计与试验结果见表1。

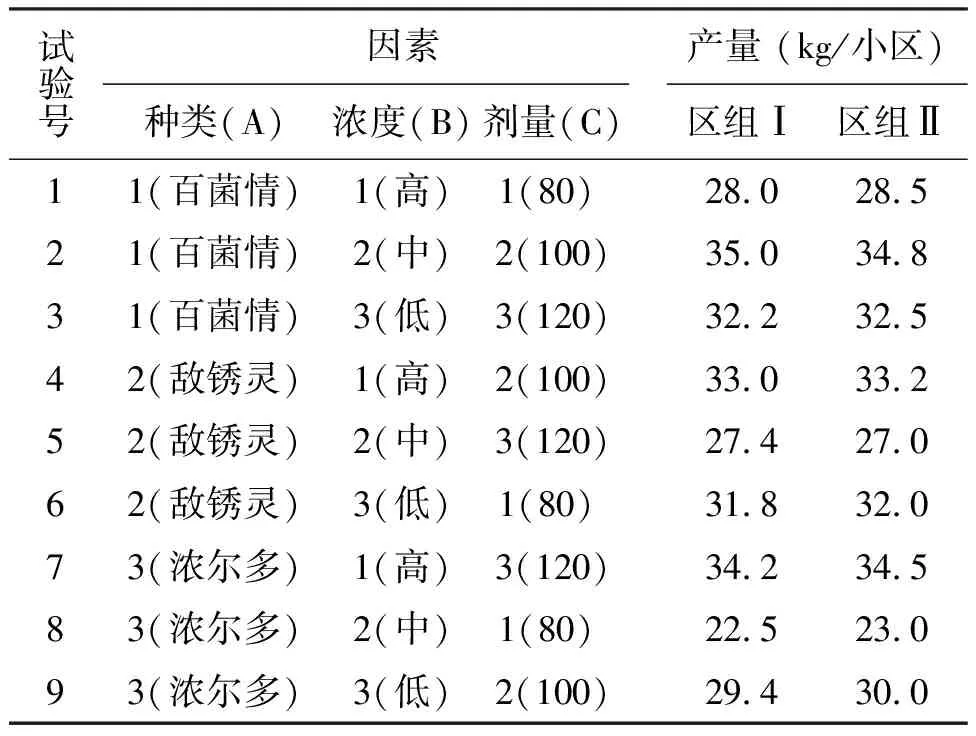
表1 防治花生锈病药剂种类、浓度、剂量正交试验方案及试验数据表[4]

1.2分析方法 通过对比分析常规正交试验分析结果，找到常规正交试验分析方法中存在的问题，针对常规分析法中的问题，采用高次多项回归模型分析同组数据，改进正交试验优选分析结果。

2 结果与分析

2.1常规正交试验设计在选优方面存在问题 在因素间没有交互作用的条件下，其各因素最大平均数对应的水平搭配应为最优组合。采用正交常规试验分析方法分析结果表明(表2)，上述试验中最优搭配为A1B1C2。但方差分析表明三因素间存在极显著的交互作用(表3)，这说明在实际情况中A1B1C2不一定为最优搭配，但最优搭配只能是在已做的9个搭配试验中选取，9个搭配试验中平均数最大的是A1B2C2搭配，因此A1B2C2应为最佳搭配。上述案例表明，在判断出存在交互作用的情况下，从已做的试验中选优是局部和有限的。

在农业科学实际生产中，各个因素间往往可能存在互作效应，因此正交试验常规分析方法确定的最佳搭配并非最佳，对因素与试验指标关系的诠释是局部的。

表2 防治花生锈病药剂种类、浓度、剂量试验数据统计

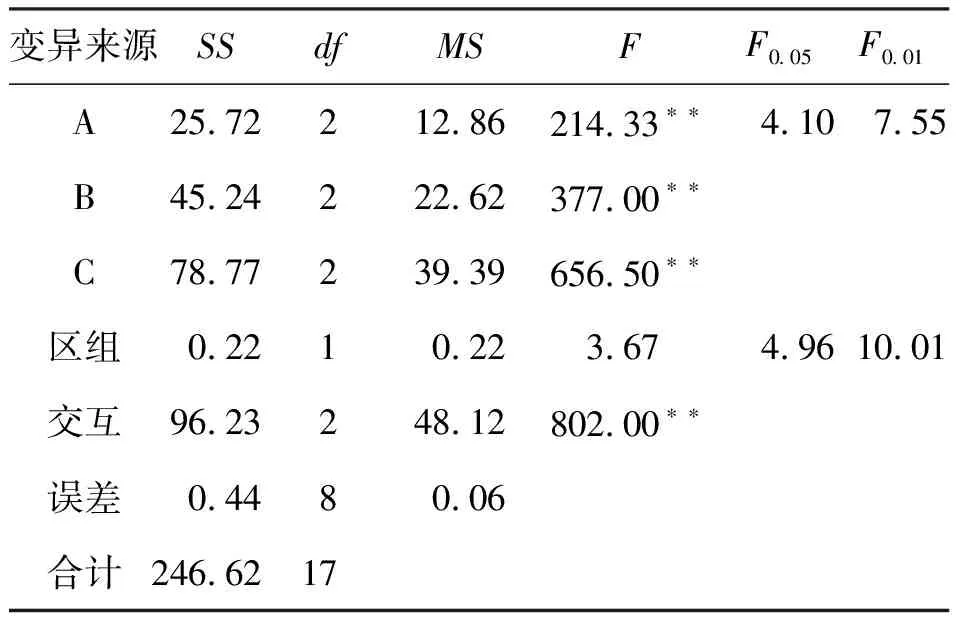
表3 重复观测值正交试验结果方差分析

2.2高次多项式回归模型对正交试验数据的优选分析 充分考虑因素间的互作效应，用部分试验估计因素与试验指标的关系，从中找出最佳搭配的思想，采用高次多项式回归模型对试验数据进行补充分析，方程中各项的选取(包括次数)采用逐步回归方法，使用Design-Expert 7.0的Response Surface进行统计运算，得到优化回归方程如下：

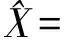
然后对回归方程进行检验(表4)。检验结果表明，回归方程中表示因素的A、B、C与试验指标X的关系是极显著的，失拟项(Lack of Fit)小，说明模型无遗漏重要项。用该回归方程模型计算的理论产量与实际产量相比，误差小(表5)，这说明回归方程与实际试验的拟合程度高。

表4 回归方程检验结果分析

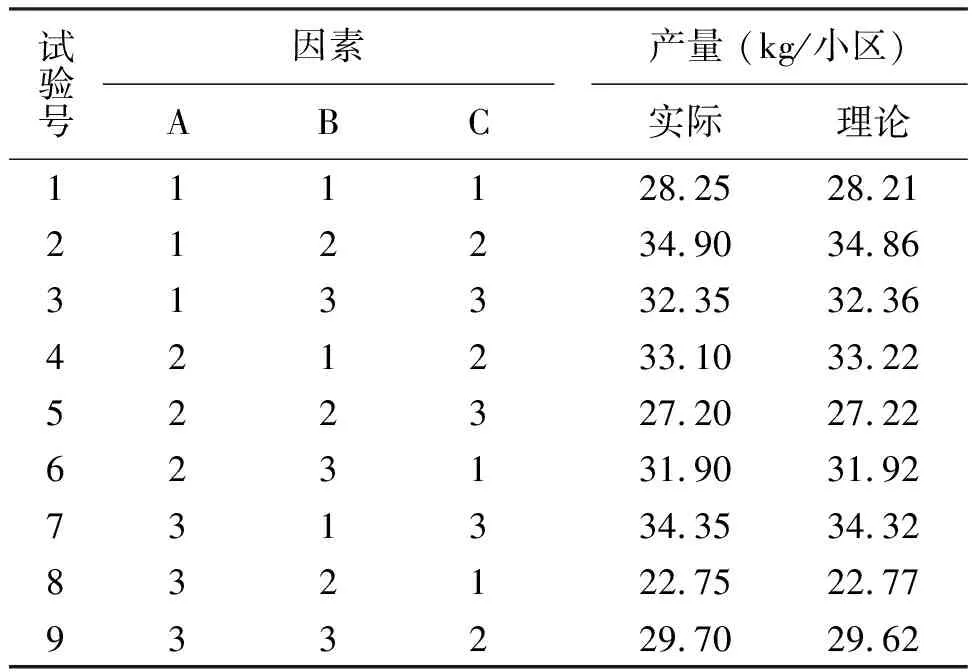
表5 防治花生锈病药剂种类、浓度、剂量的实际产量与理论产量对比

当药剂种类A=1、2、3时，从多元分析3D图形(图1)可直观地看到,药剂剂量(C)比药剂浓度(B)对产量(X)的影响大，药剂浓度B的不同对产量(X)影响小。利用回归方程可求得最大值点是(1.00,1.00,2.51)，最大值是37.937 4。因为剂量(C)是连续性的，所以优化搭配是：百菌情、高浓度、117的剂量，最后将此搭配与试验指标大的2号试验比较，进行验证性试验。

图1 不同药剂种类、剂量对花生产量的影响

以上分析表明，采用高次多项式回归模型对重复正交试验进行分析，不仅提高了理论产量和实际产量的拟合度，而且试验误差可估、可进行分析，因此更能够可靠地估计最佳搭配。

3 结论

针对常规正交试验设计选优分析方法的缺点，利用高次多项式回归模型对重复正交试验进行分析，改进了正交试验设计选优的方法，改进后的方法可以在原试验次数不变的条件下，全面诠释因素和试验指标的关系，既有效地解决因素间可能存在的交互作用造成的偏差，又有效地解决受固定水平限制的局部优化的问题，更可以利用其回归方程能够对相关问题进行全面、深入研究。因此，利用高次多项式回归分析是提高农业科学研究统计精度的方法之一。

[1] 赵选民.试验设计方法[M].北京:科学出版社,2002:64-118.

[2] 袁志发,周静芋.试验设计与分析[M].北京:高等教育出版社,2000:209-303.

[3] 明道绪.田间试验设计与统计分析[M].第二版.北京:科学出版社,2008:241-257.

[4] 彭海滨.正交试验设计与数据分析方法[J].计量与测试技术,2009,36(12):39-42.

[5] 苑玉凤.正交试验结果的分析[J].统计与决策,2006(3):138-139.

[6] 赵仁宏,贺圣文,王守训,等.多指标的正交设计及分析方法的合理应用[J].数理医药学杂志,2003,16(5):423-425.

[7] 方开泰,马长兴,李长坤.正交设计的最新发展和应用[J].数理统计与管理,1999，18(2)：44-49.