纵向配筋率对 RC矩形梁挠度及裂缝宽度的影响

2011-04-19陈惠满

山西建筑 2011年1期

陈惠满

钢筋混凝土受弯构件在工程中应用广泛，影响受弯构件正截面承载力的因素包括纵向钢筋配筋率、混凝土的强度等级、截面形式及尺寸，其中以纵向配筋率对构件抗弯承载力的影响最为明显。为了探讨纵向配筋率的变化对钢筋混凝土矩形截面梁的挠度及裂缝宽度的影响，本文根据GB 50010-2002混凝土结构设计规范[1](简称《规范》)提供的相关计算公式，分析了满足正截面抗弯承载力要求的配筋率变化对挠度及最大裂缝宽度的影响。

1 纵向配筋率 ρ对挠度的影响

根据文献[2]的推导，对于不同钢筋及混凝土强度等级的组合情况，当配筋率 ρ=As/bh0∈[0.6%，1.5%]时，其短期刚度系数 βs的表达式为:

1)梁的纵筋采用 HRB335级钢筋时:

2)梁的纵筋采用 HRB400级钢筋时:

代入 Bs=βsEcI中求得 Bs，其中，Ec为混凝土的弹性模量;I=bh3/12。对于单筋矩形截面梁的长期刚度可按式(3)计算，并根据式(4)进行挠度验算:

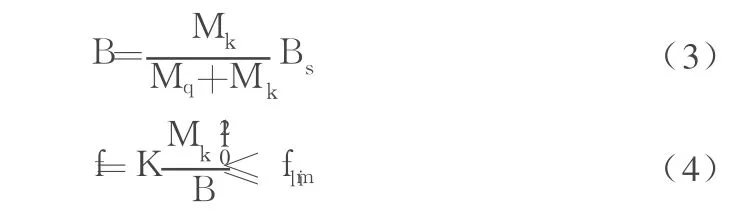
其中，Mk为按荷载效应标准组合计算的弯矩;Mq为按荷载效应的准永久组合计算的弯矩;flim为构件挠度限值;为构件计算跨度;K对于承受均布荷载的简支梁和两端固支梁分别取 5/48和1/16。

某简支矩形截面梁的截面尺寸 b×h=250 mm×500mm，计算跨度为=6 m，钢筋采用 HRB335，混凝土保护层厚度c=25mm，在均布荷载作用下，当荷载变化时要求 ρ相应变化，使得正截面抗弯承载力 Mu满足要求。试分析该梁采用混凝土强度等级分别为 C20，C 25，C30时，挠度随配筋率 ρ的变化情况。

假定 Mu=1.25Mk，Mk/(Mq+Mk)=0.8，在梁截面尺寸、材料强度等级不变的情况下，当荷载保持不变时，由式(1)，式(2)及Bs=βsEcI可知，短期刚度Bs随配筋率的增加而增大。根据长期刚度 B的计算式(3)及挠度 f的验算式(4)，可分析得，跨中挠度 f的数值逐渐减小。当荷载增大时，为了保证满足正截面抗弯承载力要求，需增大钢筋混凝土梁纵向配筋率，由于此时按荷载效应标准组合计算的弯矩值 Mk较长期刚度 B的增加幅度要大，因此跨中挠度f的数值逐渐增大，如图 1所示。可看出提高混凝土强度等级对减小梁的挠度的作用不显著。

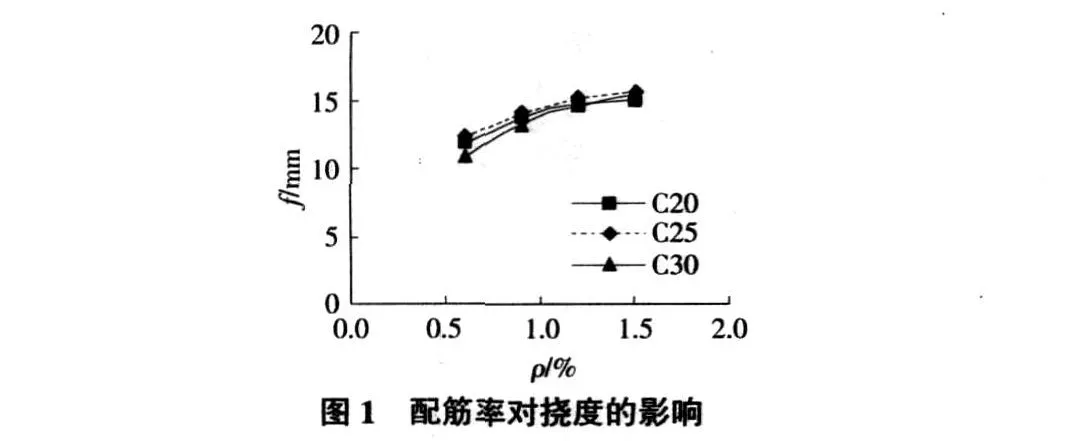
2 配筋率 ρ对最大裂缝宽度的影响

《规范》给出了矩形截面受弯构件按荷载效应标准组合并考虑长期作用影响的最大裂缝宽度验算公式:

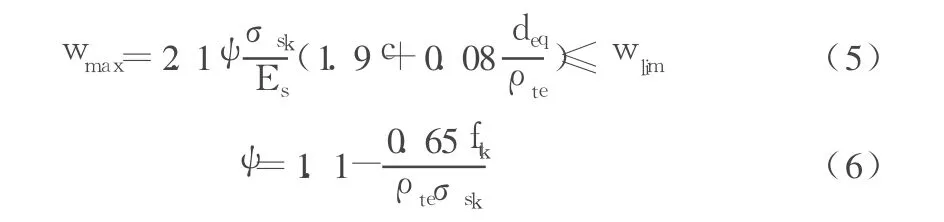
其中，各符号含义见《规范》。为了避免过高估计混凝土协助钢筋抗拉的作用，当裂缝间纵向受拉钢筋应变不均匀系数ψ＜0.2时，取 ψ=0.2;当 ψ＞1.0时，取 ψ=1.0，按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率 ρte=As/0.5bh＜0.01时，取 ρte=0.01。一般情况下，=0.93h，则当配筋率 ρ=As/bh0∈[0.6%，1.6%]时，ρte=1.86ρ＞0.01。因此在混凝土抗拉强度标准值 ftk、计算截面高度h及标准组合弯矩值 Mk已知的前提下，将 σsk=Mk/(0.87Ash0)，ρte=As/(0.5bh)代入式 (6)中得:ψ=1.1-0.283ftkbhh0/Mk。

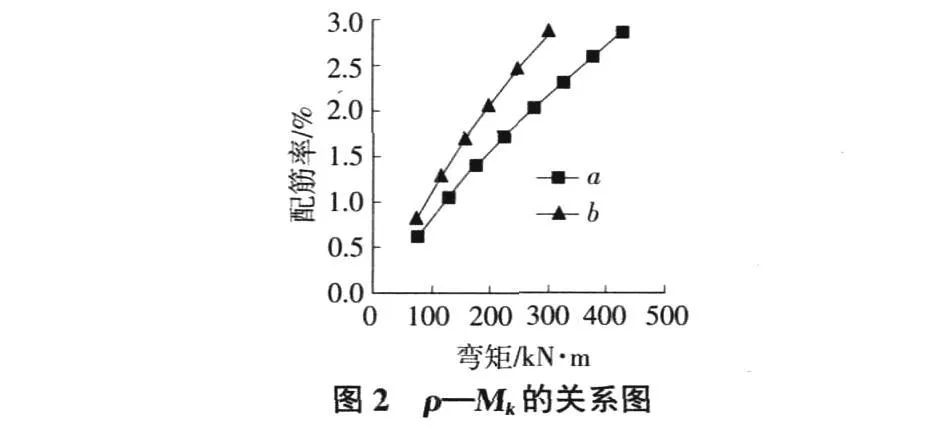
本文取梁截面尺寸 b×h=250 mm×500mm，混凝土强度等级采用 C45，钢筋采用 HRB 400，直径 d=22mm，混凝土保护层厚度 c=30mm，钢筋弹性模量 Es=2.0×105N/mm2。配筋率 ρ对Mk的影响如图 2所示。其中，a，b分别代表 wmax=0.3mm，wmax=0.2mm时对应的情况。

当最大裂缝宽度限值 wlim取不同值时，对应的配筋率 ρ的取值也将随之变化，下面分别取 wlim=0.3 mm及 wlim=0.2mm，可得出 ρ—Mk的变化趋势如图 2所示。

根据图 2可知，如果将纵向配筋率 ρ减少 21%～25%，最大裂缝宽度限值 wlim将由0.2mm增大到0.3mm。因此，在能满足《规范》要求的前提下，尽量不要故意提高相关指标值，以免造成不必要的浪费。