遗传算法在泊松曲线沉降预测模型中的应用

郑鹏

(湖北省地质勘察基础工程公司，湖北宜昌 443002)

遗传算法在泊松曲线沉降预测模型中的应用

郑鹏∗

(湖北省地质勘察基础工程公司，湖北宜昌 443002)

以某基础沉降监测数据为基础，通过遗传算法拟合泊松曲线中的参数，得到该基础沉降预测的泊松曲线模型。结果表明，所建模型与实测数据吻合较好，本文所提方法简单易行。该模型可对今后基础的沉降进行预测，也为监测设计及施工提供基础。

沉降预测；泊松曲线；遗传算法

1 概 述

地基的沉降预测问题一直受到国内外许多学者的广泛关注，是岩土工程预测热点研究问题之一。目前已提出的很多有关沉降预测的方法，主要分为两类[1～3]:第一类为数值计算方法，即将土的固结理论与本构模型结合，计算最终沉降量，如有限元法、有限差分法。第二类为通过现场实测资料(前期沉降量实测资料)进行数理分析来建立沉降量与时间关系的数学模型，从而得到相应的沉降预测模型。

数值计算方法由于其实现的复杂性，及对工程人员要求较高，掌握难度较大，不利于实际应用。第二类方法有双曲线法、指数曲线法、泊松曲线法、浅岗法、星野法、三点法、沉降速率法等[4～6]。这些方法有理论基础且简单易行，结果往往令人满意，因此，得到了较广泛的应用。但是，这些预测模型都具有非线性，对其参数的拟合具有一定的困难。

模型参数拟合问题归根到底是一个优化问题，即拟合所得参数应使预测模型与实测数据误差最小。本文以某基础沉降监测数据为基础，通过遗传算法拟合泊松曲线，得到该基础沉降预测模型，为以后的沉降预测、监测提供基础。

2 工程概况

某框架结构商住楼位于湖北省宜昌市平云二路和夷陵大道交汇处。该商住楼地下2层，地上17层，基础类型为桩基。根据规范要求和施工需要，需进行沉降监测。根据规范要求，沉降观测宜采用三等变形测量，按三等变形测量技术要求进行，沉降观测采用几何水准测量的方法。

沉降监测需布置基准点和变形观测点。基准点和工作基点布设在平云二路和夷陵大道旁。变形监测点布设在高层建筑拐角处的承重柱及中间承重柱上，共计15个沉降监测点。全部布设在承重构造柱上，±0以上40 cm～80 cm处。

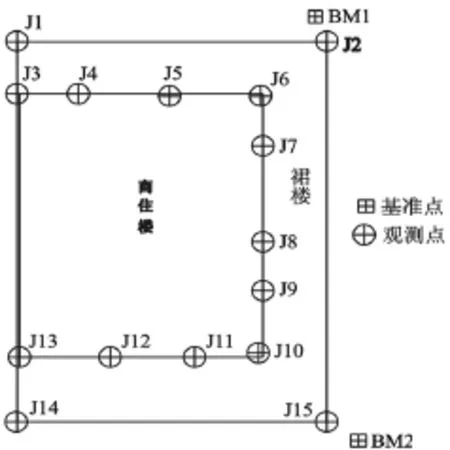
图1 沉降监测点布置平面图

对15个监测点共进行了11次监测，由监测数据知点J1的沉降量最大(限于篇幅，不列出所有监测点沉降监测数据)。故选取点J1作为典型监测点，对所测沉降数据St如表1所示。

点J1沉降量监测数据表 表1

3 泊松曲线模型

地基沉降的泊松曲线预测模型函数表达式为:

式中，Ft为t时刻对应的预测沉降值，单位为mm；t为时间，单位为d；A，B和K为待定参数且为正值。由式(1)可知，模型共有3个未知参数，可由观测数据{(ti，Sti)}来确定。一旦参数确定，即可建立泊松曲线方程，进而可以对以后的沉降进行预测。

4 遗传算法确定泊松曲线模型

遗传算法是在20世纪60年代末期到70年代初期，由美国Michigan大学John H.Holland教授与其同事、学生们研究形成了一个较完整的理论相方法，它是从解释自然系统中生物的复杂适应过程入手，模拟生物进化的机制来构造人工系统的模型[7]。遗传算法的基本过程见图2。

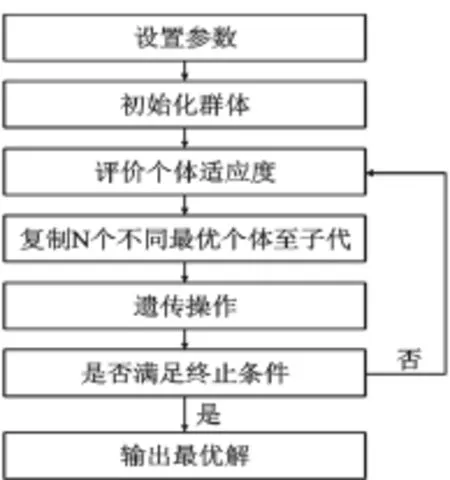
图2 遗传算法流程图

应用遗传算法对式(1)中参数A，B和K进行优化，使所得预测模型与实测误差最小。本文中设定个体为向量(A，B，K)，每个向量对应一个泊松曲线模型。设定A∈[14，16]，B∈[0，0.1]，K∈[1.0，2.0]。

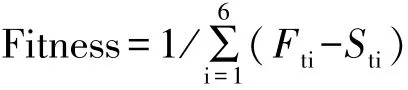
式中，Fitness为个体适应度；Fti为个体所对应泊松曲线模型的预测值；Sti为实测值。

遗传算子包括选择、复制、交叉、变异。对于选择算子用轮盘选择法。对于选定的个体，复制算子为将父代直接移至子代；本文未设置变异算子；对于交叉算子则按式(4)计算:

式中:v1′，v2′为子代个体，即执行交叉运算后的个体；v1，v2为随机选择的两个父代个体；α为[0，1]之间的随机数。

本文设定群体规模为50，个体随机产生。复制算子概率为0.75，交叉算子概率为0.25，不设置变异操作。最大遗传代数为5 000。最终所得最优个体为(10.00，0.034 1，1.410)，即对应的泊松曲线模型为:

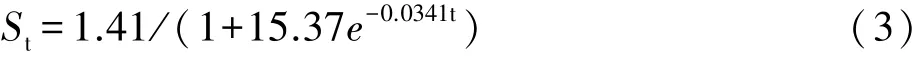
为检验预测模型的正确性，将实测数据与预测数据列于表2。

由表2可知，本文所建立的沉降预测模型在拟合沉降监测实测数据时，初期误差较大，如T＝0 d时刻；中期误差较小；中后期误差有一定增大；最终沉降量是一致的。

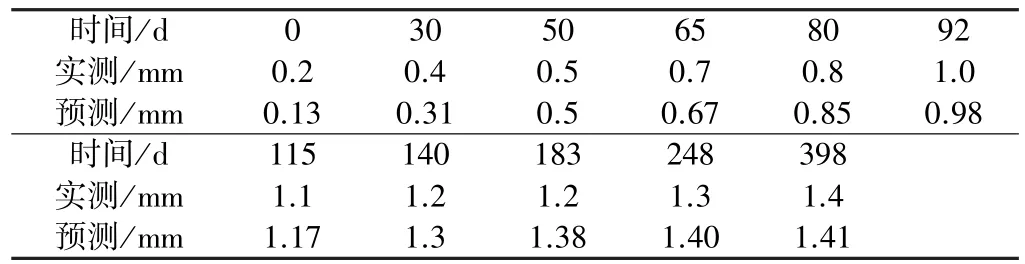
点J1沉降量实测与预测对比表 表2

5 结 论

本文以某基础沉降监测数据为基础，通过遗传算法优化泊松曲线中的参数，得到该基础沉降预测模型。结果表明本文所提方法可靠，简单易行。本文为该项目以后的沉降预测、监测提供基础，并对该地区类似工程具有一定的参考借鉴意义。

[1] 金开正，袁俊.地基沉降预测模型的探讨[J].中国市政工程，2006，1:76～77

[2] 李刚，王福胜，何晓霞.公路软基路堤实测沉降资料的分析方法[J].路基工程，2006，2:71～73

[3] 张振武，徐晓宇，王桂尧.基于实测沉降资料的路基沉降预测模型比较研究[J].中外公路，2005，25(4):26～29

[4] 贾丽杰.双曲线预测复合地基沉降量的合理性研究[J].交通标准化，2005，154:l～3

[5] 辜清华，何良德.预测路基沉降的一种新模型[J].石家庄铁道学院学报，2006，19(2):64～76

[6] 宰金眠，梅国雄.全过程的沉降量预测方法研究[J].岩土力学，2000，21(4):322～325

[7] 许小健.遗传算法在岩土工程学科非线性优化中的应用[D].合肥:合肥工业大学，2007.11

The Application of GA in Parameter Fitness of Poisson’s Prediction Model for Settlement

Zheng Peng
(Geological Investigation＆Foundation engineering Company，Yichang 443002，China)

Based on the monitoring data of one foundation，the parameters of Poisson’s prediction model for settlement are fitted by GA.Calculations show that the model agree well with monitoring data and the method proposed in this paper is feasible and simple.This model could provide basic data for monitoring design and prediction of foundation settlement.The paper has a certain reference value for similar work.

settlement prediction；Poisson’s curve；GA

1672－8262(2011)01－172－02

P209

B

2010—04—28

郑鹏(1967—)，男，工程师，主要从事岩土工程监测应用与研究工作。