一种简单可靠的昆虫扑翼运动图像序列自动分析方法

魏 榛,杨基明,C.P.Ellington

(1.中国科学技术大学,安徽合肥 230027;2.剑桥大学,英国 CB2 3EJ)

0 引 言

昆虫飞行的运动学描述一直是扑翼飞行空气动力学研究所需的重要信息。高速摄影则是获得昆虫扑翼运动细节的绝佳工具。如今,昆虫观测中高速相机拍摄速度已达到1000fps以上,一次可存储上千帧昆虫运动的数字图像。此时采用人工逐帧提取图像中昆虫形态学特征的方法[1]来分析数据显然不可取,开发一种能够自动分析海量昆虫扑翼运动图像的方法十分必要。

然而,昆虫运动图像的复杂性和经典运动图像识别技术的局限性,使得实现这样的自动分析非常不容易。首先,昆虫图像轮廓十分复杂：真实昆虫翼面不仅具有挥拍角、迎角和偏斜角的变化还具有扭转和弯曲变形[2-3],而且昆虫身体还有其自身的运动姿态。其次,扑翼运动的某些时刻翼面图像和昆虫身体图像间会发生部分遮挡。再次,昆虫翼面本身的透明性使得翼面图像和背景十分接近。再则,每帧图像都需要同时提取多个形态学特征：左右翼面各自的翼尖、翼根点,前、后缘轮廓,身体的头部和腹部端点等。最后,经典的运动图像识别方法直接处理昆虫图像问题大都有局限：如基于背景提取的模板匹配方法[4-5]虽然可以适应遮挡、透明和噪声等问题,但较难适应昆虫图像轮廓的柔性大变形;而光流法[7]可以克服柔性大变形影响,却无法较好处理遮挡、透明和噪声等问题。

为了构建一种切实可用的,无需人工干预,不针对特定昆虫,运算量也较小的昆虫扑翼图像自动分析方法,经过对昆虫扑翼运动图像的内在特点的分析,独辟蹊径地提出了一种完全不同于经典运动图像识别方法的新方法,并尝试了使用程序合成的虚拟昆虫运动图像和真实昆虫的运动图像测试该方法。

1 基本假设和图像处理流程

昆虫图像的形态学特征提取是获得昆虫飞行的运动学描述十分基本而关键的步骤：单相机观测系统得到昆虫形态学特征后即可使用对称假设[1,8]等求出运动学描述;多相机系统得到每个相机视角的昆虫形态学特征后,即可通过对应特征的空间匹配[5-6,9-10]求出运动学描述。因此,这里不讨论具体的观测系统,而是解决单个视角昆虫图像上的自动昆虫形态学特征提取这一基本而关键的难题。为了实现所提出的处理方法,对于选取的昆虫图像需要满足一些简单的假设。

首先,图像序列中昆虫的身体和翼面间的遮挡不能太严重。严重遮挡的时候,不便于同时提取两翼面的形态学特征。其次,相邻两帧图像间的翼面位置变化要大于昆虫身体的位置变化。再次,图像中翼面前缘轮廓线与翼面后缘轮廓线只在翼尖点和翼根点相交,即不考虑翼面严重扭转的情形。最后,假设昆虫身体部分只发生刚性运动,且昆虫头部端点到翼根点的距离要小于昆虫腹部端点到翼根点的距离。

选取合适的相机角度和拍摄速度,上述假设对于果蝇,黄蜂,鹰蛾等昆虫都较容易满足。得到图像序列之后,首先需要获得每帧图像中昆虫部分的二值图,然后再根据得到的二值图计算昆虫的形态学特征。与经典运动图像处理方法截然不同：这里采用了相邻三帧图像的巧妙运算来实现昆虫翼面和身体的二值图提取,借助了昆虫内在特征和上述假设,实现从二值图逐一自动分析所需的多个昆虫形态学特征。

2 昆虫翼面和身体二值图的提取

为得到昆虫翼面和身体的二值图,利用了相邻三帧图像的差别。此方法既克服了经典运动图像识别中直接二值图提取时无法应对昆虫翼面图像与背景反差太小的问题,又克服了背景静止图像对二值图提取时的干扰。其独到过程如下图1所示。

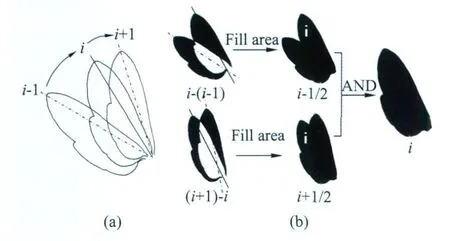
图1 翼面二值图提取原理Fig.1 Principle of wing binary image extraction

翼面二值图提取的操作原理如图 1所示：图1(a)表示从i-1到i+1时刻连续的三帧昆虫翼面轮廓关系;图 1(b)中,把第i-1与i帧的灰度图像相减并二值化得到的图像标号记作i-(i-1),其中白色部分为相邻两帧间翼面因重叠被减去的部分。然后使用图像形态学算法可以填充这个白色区域部分,得到的图像标号记作i-1/2;标号i+1/2的图像提取的方法完全类似。最后,对标号i-1/2和i+1/2的翼面二值图进行“与”操作,即得到i时刻昆虫翼面部分的二值图。

此方法巧妙地使用了两次相邻帧的相减图像的二值化操作来提取中间帧的二值图。因为是从相减图像中恢复原图像信息,所以不需要使用背景图像的灰度估计等,也就避免了翼面与背景反差太小时经典运动图像处理方法的直接二值化困难。同时,经典的图像处理方法只使用一次相邻帧的相减图像的二值化操作来估计运动目标的大体位置,这实质上并没有充分地利用帧间相减图像的二值图所包含的全部信息。使用两次相邻帧的相减图像的二值化操作,则充分利用了相减图像的二值图信息,可以直接还原出中间帧的二值图,因而与图像中翼面如何变形无关,这也避免了经典图像处理方法中模板匹配时不适合柔性大变形的难处。当然,图1是在理想情况下的操作过程,实际使用中还必须考虑真实图像二值化的方法和图像形态学处理的技巧。

相邻两帧图像相减时,所得灰度图像反映了相减图像间的灰度变化;对于昆虫运动图像而言,相邻两帧间的最大差别来自于翼面运动所带来的灰度变化。由于相邻两帧图像中翼面变化并不大,翼面灰度与背景灰度差别也不大,所以相减所得的图像的灰度动态范围较小,因此先要增强相减图像上翼面运动区域所代表的灰度特征。设相减图像中一共有k阶灰度,第i阶灰度值为gi,具gi灰度值的像素个数为Ni,增强之后的加权灰度值Gi由下式计算

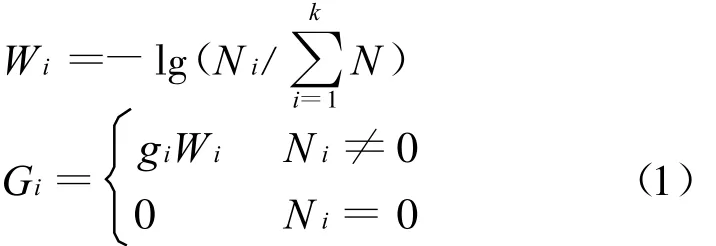
公式(1)所构造的灰度值权重函数W是一个与像素个数比的对数成反比的函数,即相减图像上具有某个灰度值的像素个数占图像总像素个数的比例越高,就越不可能是翼面运动有关的部分所在的像素,而相减图像上那些灰度值较大且像素个数较少的像素则最有可能反映翼面的运动区域,在公式(1)中也取得了较大的灰度权重而被图像增强。显然这与相减图像的物理直观一致,比经典图像处理方法中的简单二值化方法更能强化图像中所包含的运动和轮廓信息。

增强处理之后,相减图像能够充分地反映翼面运动区域的灰度特征,再取阈值进行相减图像的二值化,就可得到较完整的相减图像的二值图,即图1中的标号为i-(i-1)的图像或标号(i+1)-i的图像。

以标号i-(i-1)的图像为例,分析得到标号i-1/2的图像的形态学处理技巧。真实图像由于翅脉的灰度反差与翼面部分十分不一致或相减图像的二值化阈值选取偏差,所得到的标号i-(i-1)的图像一般会出现连通区域破碎。这时图像形态学处理进行适当修补,处理过程如图2所示。

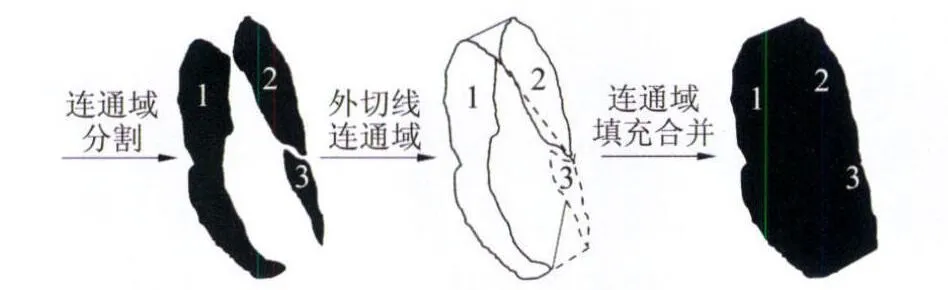
图2 中间过程二值图的形态学操作Fig.2 Morphological operation of the binary image in process

首先通过连通域分割得到二值图的分块结果如图2按面积由大到小编号为1,2,3…;然后,借助轮廓操作对每个分块区域求取与编号1区域的外切线连通域;最后填充生成的连通域,再“并”操作即得到标号i-1/2的图像。经典的运动图像处理方法中,对于标号i-(i-1)的图像一般不会采取如图2的深入处理,因为经典的运动图像处理方法并非基于相邻三帧图像的两次图像相减的,而在独辟蹊径的巧妙方法中,图2的图像形态学操作使得最终标号i-1/2的图像与标号i+1/2的图像的“与”操作成为可能。

经过“与”操作之后,第i帧图像中的昆虫翼面二值图已经成功提取出来。不难发现,本方法巧妙地回避了正面解决昆虫图像轮廓柔性大变形和昆虫图像质量不佳等问题,独辟蹊径把轮廓提取问题简化成两次相邻帧的相减图像的二值化操作为核心的简单处理过程,因而能够处理经典运动图像处理方法所不适合的难题。

由于昆虫身体不透明,因而与图像背景反差鲜明;所以得到第i帧的昆虫翼面二值图之后,直接在第i帧原图像中扣除翼面二值图部分,再对原图像中翼面二值图所在的局部区域进行二值化即可得到昆虫身体部分的二值图。第i帧的昆虫翼面二值图已经获得,所以不仅昆虫所在区域已经确定,而且扣掉翼面原图部分之后,昆虫身体的二值图提取就不再有来自翼面灰度的干扰,所以难度大大降低。

3 昆虫形态学特征提取

得到各帧的昆虫翼面和身体二值图后,即可提取昆虫形态学特征。经典图像处理方法中,基于背景提取的模板匹配方法如果已经完成匹配,那么就可以从用于匹配的参照模板图像上直接获得昆虫的形态学特征。然而模板匹配方法首先面对此难题就很难实现图像匹配;就算得到匹配图像,也是基于特定昆虫的匹配,无法适应非特定昆虫的识别要求。而另一类经典运动图像处理方法如光流法,且不计较难以处理具有遮挡、透明和噪声等问题的昆虫图像,即使得到轮廓结果,仍然也需要设计方法来进行昆虫形态学特征的分析,并无捷径可走,因此与本方法相比并无优势。根据所述方法已经分离出第i帧的翼面二值图和昆虫身体二值图,因此,昆虫形态学特征的提取成为可能。昆虫形态学特征提取过程如图3所示。

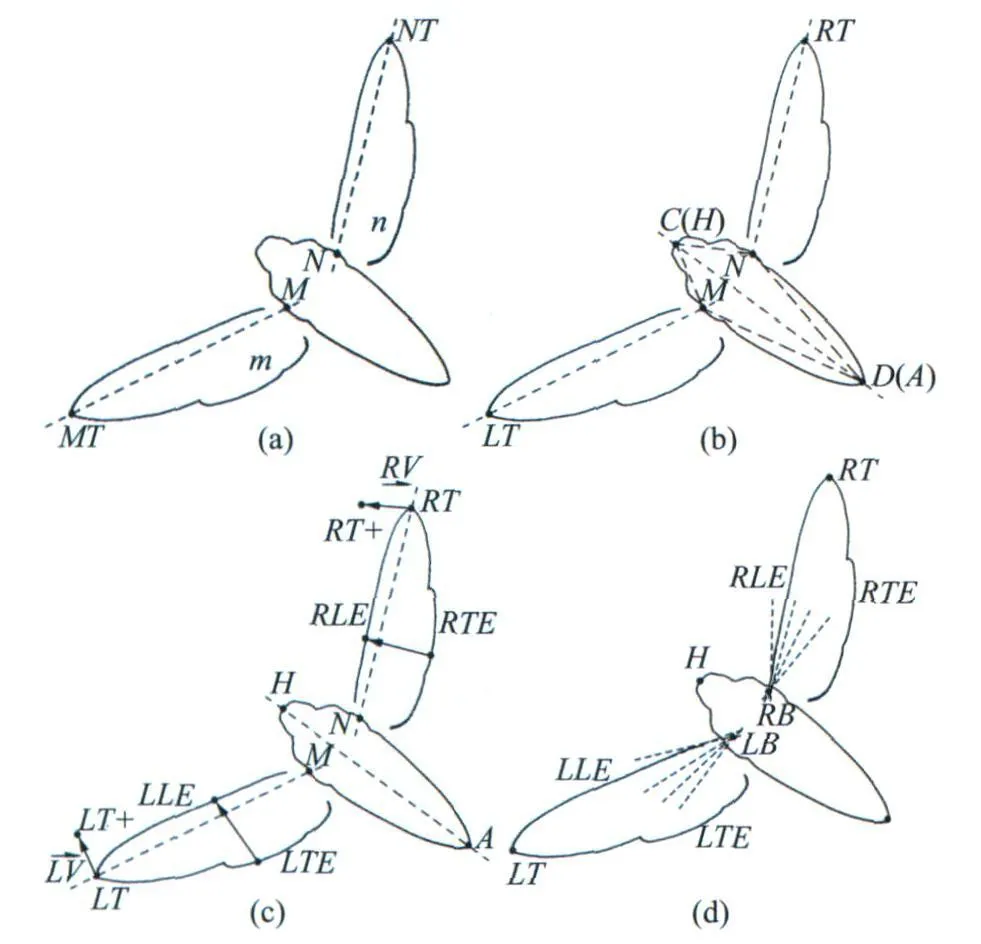
图3 昆虫形态学特征提取步骤Fig.3 Step of insect morphology feature extraction

由于使用了常见昆虫的内在特征作为形态学特征提取的依据,因此对于满足这些特征的昆虫,这种形态学提取方法都是可靠的。也正因为此,所以所提供的形态学特征提取方法是不针对特定昆虫的,也是无需人工干预的,这大大优于经典的匹配的方法。

4 测试结果

采用了由程序合成的虚拟昆虫运动图像和真实的昆虫运动图像来完成测试上述的方法。程序合成的虚拟昆虫运动图像用于验证结果的正确性,真实的昆虫运动图像用于验证该方法的实用性。

程序合成的虚拟昆虫图像使用了MATLAB生成,基于理想相机模型的投影关系,模拟了俯视相机角度的悬停飞行的鹰蛾多个挥拍周期的运动。虚拟图像如图4所示。

由于图像序列为程序合成,所以预先知道虚拟昆虫的形态学特征,因此能够对比本方法自动处理得到的形态学特征。形态学特征点的比较结果以X,Y方向的误差像素大小来衡量,形态学特征轮廓的比较结果以轮廓的平均误差像素来衡量。此处合成了600×800分辨率,90帧,共3个扑翼周期的灰度图像用于测试,最后的误差结果如图5所示。

图4 程序合成的虚拟昆虫运动图像截图Fig.4 Motion video clip of the virtual insect generated by program

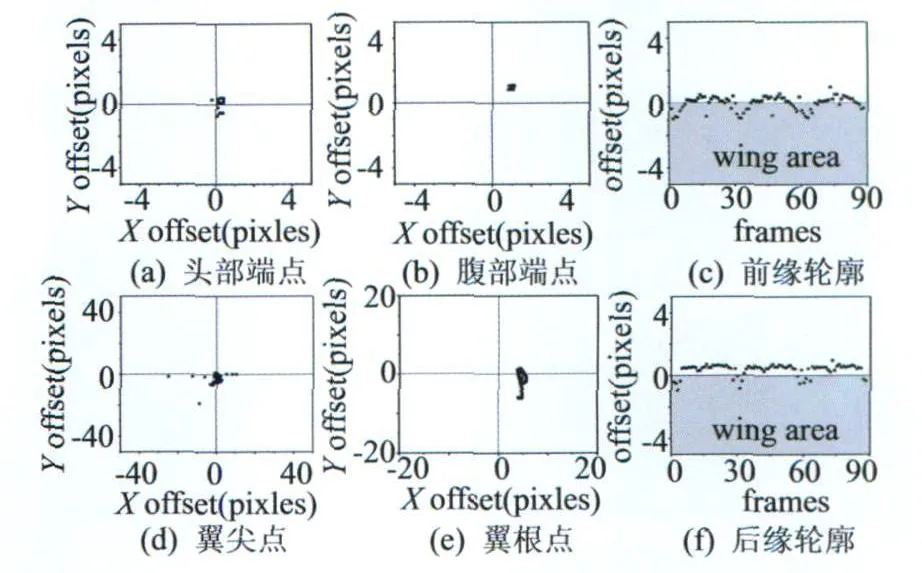
图5 虚拟昆虫处理结果的误差分布Fig.5 Error distribution of virtual insect result

图5只列出左翼的误差结果,右翼结果类似。虚拟图像中昆虫身体长度约为174个像素,挥拍幅度150°左右,上图可见,虚拟昆虫头部和腹部端点识别结果平均误差在0.6%的昆虫身体像素左右;翼尖识别结果除去少数几帧因为翼尖位置太靠近身体部分而在X方向上识别误差较大外,平均误差在4.2%的昆虫身体像素左右;翼根点识别使用了拟合方法,因此误差呈现较规律的分布,平均误差约在2.9%的昆虫身体像素左右;翼面前缘和后缘轮廓平均误差都控制在较小范围,大约在0.4%的昆虫身体像素左右。综上可知,在虚拟昆虫图像上本方法能够给出较好的识别结果。因为虚拟昆虫图像不能很好地模拟真实高速摄影图像效果中的背景噪声,图像轮廓模糊等情况,因此需要真实昆虫图像作为进一步的测试。

测试所使用的真实昆虫运动图像是在进行偏航角调整的机动飞行过程中的长尾管蚜蝇(Eristalis tenax)俯视图像,一共150帧,600×800分辨率,拍摄速度为4700f/s。图6为真实昆虫运动图像部分帧的截图。

使用本处理方法进行自动分析,即可得到昆虫的形态学特征。处理程序运行于MAT LAB V7.5,一共处理得到148帧图像中的运动特征,平均每帧画面运算耗时8.45s,图7列出了图6中的图像帧的处理结果。

从图6的图像可见,昆虫左右翼的运动非常的不对称;除前缘之外的昆虫翼面灰度都十分接近背景灰度;帧编号fn=100的图中右翼面较为靠近昆虫身体。而图7所得提取结果在这些情况下都能较为准确地判别昆虫的特征点和翼面轮廓。由此可知,独辟蹊径所采用的二值图和形态学特征提取方法对于真实昆虫图像能够自动分析给出较好的结果,这已经克服了经典运动图像处理方法在昆虫运动图像处理上的难度,具有实用价值。由各帧所得的形态学特征数据进一步可以绘制出图像坐标系下昆虫身体头尾连线角度和两翼面与身体夹角的变化曲线,如图8所示。

图6 真实昆虫运动图像截图(fn,fn为帧编号)Fig.6 Motion video clip of real insect

图7 真实昆虫图像的形态学特征提取结果Fig.7 Morphology feature extraction result of real insect

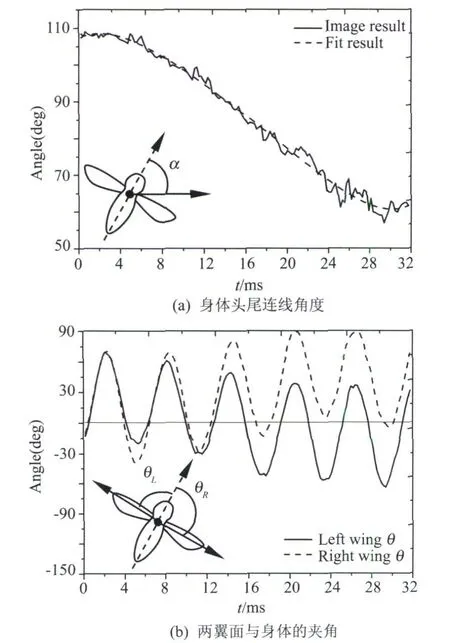
图8 真实昆虫形态学特征角度变化Fig.8 Morphological feature angle curve of real insect

图8中的 α,θL,θR并非严格意义下的昆虫身体空间姿态角和翼面挥拍角,但却能够充分反映图像上昆虫姿态的变化。图8可知,一方面在接近30ms的时间内昆虫翼面完成了5个周期的挥拍运动,且左右翼面极不对称的运动使得昆虫身体获得了约50°的偏航角调整;另一方面图8曲线是直接使用图像提取的形态学特征进行绘图的结果,未经过后期滤波等处理,可知根据形态学特征来计算的角度变化较为平滑,能够充分地反映图像中的昆虫的运动过程,再次证明了所提供的方法能够自动提取较为准确可靠的形态学特征。

5 结 论

程序合成的虚拟昆虫运动图像和真实昆虫的运动图像的测试结果表明：该方法简单可靠,无需人工干预,不针对特定昆虫,运算量也较小,并能够提供较好的识别结果。这给昆虫图像的形态学特征自动识别难题提供了一个切实可行的解决方法,极大地节省了昆虫扑翼运动图像的分析时间。

该方法独辟蹊径,采用了相邻三帧图像的巧妙运算来实现昆虫翼面和身体的二值图提取,借助了昆虫内在特征和简单假设,实现从二值图逐一自动分析所需的多个昆虫形态学特征,完全不同于模板匹配或光流法等经典的运动图像分析方法。事实证明该方法能够较好地适应于昆虫这种复杂变形体运动,并能够在翼面透明,昆虫身体有遮挡,高速摄影本底噪声大的环境中,顺利地自动提取二值图并分析形态学特征。采用本文所提供的方法可以更加高效便捷地分析昆虫飞行的运动学特征,这对于昆虫飞行的空气动力学研究将很有帮助。

[1] ELLINGTON C P.The aerodynamics of hovering insect flight[J].III.Kinematics Philosophical Transactions of the Royal Society of London Series B-Biological Sciences,1984,(305)：41-46.

[2] CHENG P,HU J,ZHANG G F,et al.Deformation measurements of dragonfly's wings in free flight by using windowed fourier transform[J].Optics and Lasers in Engineering,2008,(46)：157-161.

[3] WALKER S M,WALKER S M,THOMAS L R,et al.Deformable wing kinematics in free-flying hoverflies[J].Journal of the Royal Society Interface,2010,(7)：131-142.

[4] HENIKOFF J,SHAPIRO L G.Representative pat-terns for model-based matching[J].Pattern Recognition,1993,(26)：1087-1098.

[5] FONTAINE E I,ZABALA F,DICKINSON M H,et al.Wing and body motion during flight initiation in Drosophila revealed by automated visual tracking[J].JEB,2009,(212)：1307-1323.

[6] 赵创新,徐进良,张永立,等.基于单摄像机的昆虫自由飞行参量三维重构[J].光学学报,2006,(26)：61-66.

[7] BARRON J L,FLEE D J,BEAUCHEMIN S S,et al.Performance of optical-flow techniques[J].International Journal of Computer Vision,1994,(12)：43-77.

[8] WILLMOTT A P,ELLINGTON C P.Measuring the angle of attack of beating insect wings：Robust three dimensional reconstruction from two dimensional images[J].JEB,1997,(200)：2693-2704.

[9] WALLACE I D,LAWSON N J,HARVEY A R,et al.High-speed photogrammetry system for measuring the kinematics of insect wings[J].Applied Optics,2006,(45)：4165-4173.

[10]FRY S N,DICKINSON M H.Kinematics and aerodynamics of free flight maneuvers in Drosophila[J].A-merican Zoologist,2001,(41)：1447-1447.