非凸边界上自然单元法形函数计算方法研究

张 欣

0 引言

有限单元法在计算力学及其相关工程领域得到了广泛的应用，但由于其结点之间必须连接成相关的单元，因此在处理诸如裂纹扩展、大变形等问题时因网格的变形和扭曲而影响解的精度甚至造成求解困难。近年来兴起的无网格方法的主要优点是不必将所研究的区域划分为网格，但由于很多无网格方法的近似函数不具备插值性质，因而有准确施加本质边界条件的困难。

较晚出现的自然单元法(NEM)[1]，在凸区域的边界上其形函数可以满足 δ函数性质并具有线性插值性，在非凸边界上则需要采用α-shape方法[2]或约束自然单元法(C-NEM)[3]来计算形函数，但这两种方法在实施时存在诸多限制和不便之处。

本文就非凸边界上自然单元法形函数插值性能及其计算方法进行了研究和探讨，在揭示了造成非凸边界上形函数不在边界结点间线性变化的原因及其本质的基础上，提出了一种新的非凸边界上自然单元法形函数计算方法，实现了形函数在边界结点间的线性变化，对结点布置和区域边界的凹凸程度并无限制，对各种形式的凸或非凸边界计算方法是统一的。

1 自然单元法与自然邻点插值

自然单元法是以自然邻点插值作为试函数的求解偏微分方程的数值方法，Sukumar等在文献[4]中将自然单元法应用于二维弹性力学问题的研究。

Sibson[5]利用Voronoi图和二阶Voronoi单胞的概念定义了点x的自然邻点坐标。对图1的二维情形，点x对于结点I的形函数为:

其中，AI为计算点x与其自然邻点I对应的二阶Voronoi单胞的面积。如图1所示，点x与其自然邻点4对应的二阶Voronoi单胞是四边形abfe所围成的区域。

Non-Sibson[6]插值是较晚提出的一种基于Voronoi图的插值方法，对于图1的情形，点x对于结点I的non-Sibson插值形函数定义为:

其中，sJ(x)为计算点x与结点J相关的Voronoi边的边长; hJ(x)为计算点x到结点J的距离的一半;n为点x的自然邻点个数。

在凸区域的边界上，由于计算点与边界结点相应的二阶Voronoi单胞的面积趋于无穷，因此在凸区域的边界上计算点x的形函数仅当其自然邻点为边界结点时才不为 0，且为计算点坐标的线形函数。但是在非凸区域的边界上，由于边界结点的Voronoi单胞面积(三维时为体积)不再是无限的，因而插值函数在边界节点间不再是线形变化的。

Cueto E等[2]使用建立点集α-shape的方法来构建非凸区域的模型，以实现在非凸区域边界上位移场是线性变化的，并称这种方法为α-NEM。在计算力学中往往需要在场变量变化剧烈的地方加大布点密度，这种情况下点集的α-shape不一定能重构区域的真实形状，如此又引出了随密度变化的α-shape，即α值随局部的点的分布密度而变化。因此布点密度的变化不仅是计算精度的需要，也是模拟计算区域几何模型的需要。

Yvonnet J等[3]通过引入可见性准则来建立点集的约束Voronoi图，并以此作为形函数计算的依据，实现了近似函数在非凸边界上的线性插值，这种方法特别适用于具有裂纹边界的非凸区域，称为约束自然单元法(C-NEM)。

非凸边界上自然单元法形函数计算的α-shape方法和C-NEM方法各有其优点和不足。α-shape方法需要对结点布置加以控制，且对高度非凸边界如裂纹尖端等情形是不适用的。C-NEM方法通过定义点集的约束Voronoi图来限制相应的邻点关系，比较适合于具有裂纹或材料边界的情形，但对于复杂边界其计算复杂性和计算量都较大。本文提出一种计算非凸边界上自然单元法形函数的统一方法，在明确定义边界结点的基础上，通过简单的局部判定来限制相关的邻点关系，从而实现在非凸边界上形函数的线性变化和近似函数在边界上的线性插值。相对于 α-NEM和C-NEM，将本文方法称为边界结点法(B-NEM)。

2 非凸边界上自然单元法形函数计算的边界结点法

影响形函数计算的因素是计算点的自然邻点和相关结点的自然邻点。为了使形函数在边界结点间是线性变化的，边界上的计算点x的Voronoi单胞在边界线的外侧应该是无限的。由于非凸边界上的计算点实际上是位于原点集凸壳的内部，因而其Voronoi单胞总是有限的，而从另一个角度来看，引起这一现象的根本原因是非凸边界上的计算点一定有位于其所在边界线段外侧的自然邻点。

边界结点法的基本思想是通过边界结点确定边界线段，且边界线段是有向的，任一点x位于边界线段ij的内侧是指按照i，j，x的循环次序所定义的三角形的有向面积为正值。通过限制位于边界线段外侧的结点成为计算点的自然邻点，可以实现边界上计算点的Voronoi单胞在边界线段的外侧是无限的，事实上通过局部边界线段来限制相关点对的邻点关系可以满足可见性准则的要求。

如图 2所示，需要限制边界线段 12外侧的结点 3和结点4成为计算点x的邻点，为了保证形函数计算的连续性，结点 3，4也不应成为位于△125外接圆内且位于边界线段 12内侧的计算点的邻点。注意到结点 3，4位于边界线段 12的外侧与计算点x位于边界线段 31的外侧是等效的，因此可以通过判断计算点x位于边界线段 31的内侧还是外侧来决定结点 3，4能否成为其邻点，换句话说边界线段 12外侧的结点 3，4不能以越过边界的方式影响计算点x的形函数计算。

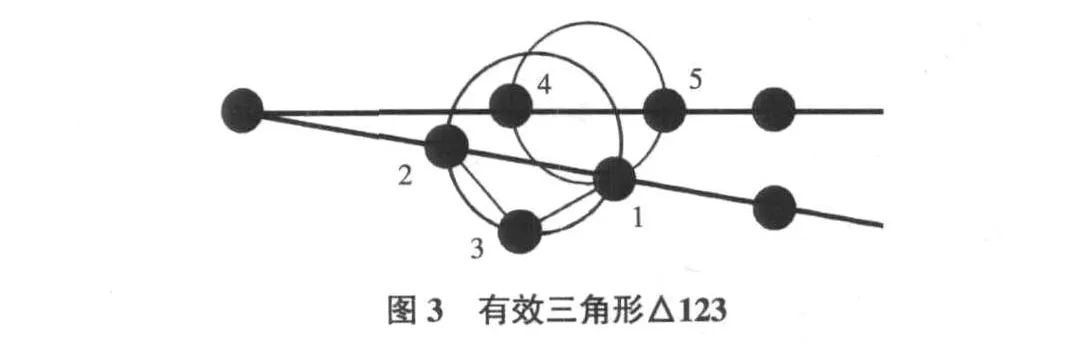
另一个需要处理的问题是计算区域的三角化应该能准确反映区域的边界形状，这可以通过允许空外接圆包含相应边界线段外侧的结点来实现。图 3中△123的外接圆包含位于边界线段外侧的结点 4，因此△123是有效的，但是应该禁止△541成为有效的三角形，因为结点 1位于边界线段 45的外侧。

3 算例

考虑图 4情形，区域包括了两类非凸边界情形，一类是在裂纹分析中可能出现的高度非凸的边界，另一类是一般的非凸区域，为了使边界显示的更加清楚，在裂纹边界处有意地使裂纹两侧的边界进行了一定程度的分离，事实上裂纹两侧的边界结点位置也可以是重合的，但需要进行不同的结点编号。两个不同结点1，13的形函数计算结果见图 5，限于篇幅未示出形函数的导数的计算结果。

4 结语

为实现非凸边界上自然单元法形函数在边界结点间的线性变化，本文提出通过边界结点确定相应边界线段的内外侧，以简单的局部判断避免在三角化时出现跨越边界的三角形，在形函数计算时避免结点以跨越边界的方式影响形函数的计算，实现了形函数在边界结点间的线性变化。通过对多种形式的边界进行实际计算，结果显示无论对凸边界、一般非凸边界、裂纹边界、材料边界以及内部结点比较接近于边界时的情形，计算所得形函数在边界线段上是线性变化的，且采用的方法或判断准则是一致的。因此本文方法具有方便实用、适用面广和计算方法统一等特点，为自然单元法的进一步应用奠定了坚实的基础。

[1] Braun J，Sambridge M.A Numerical Method for Solving Partial Differential Equations on Highly Irregular Evolving Grids[J]. Nature，1995(376):655-660.

[2] Cueto E，DoblaréM，Gracia L.Im posing essential boundary conditions in the natural neighbour Galerkin method by means of density-scaledα-shapes[J].International Journal for Numerical Methods in Engineering，2000(49):519-546.

[3] Yvonnet J，Ryckelynck D，Lorong P，et al..A new extension of the natural element method for non-convex and discontinuous problems:the constrained natural element method(C-NEM) [J].International Journal for Numerical Methods in Engineering，2004(60):1451-1474.

[4] Sukumar N，Moran B，Belytschko T.The Natural Elements Method in Solid Mechanics[J].International Journal for Numerical Methods in Engineering，1998(43):839-887.

[5] Sibson R.A Vector Identity for the Dirichlet Tesselation[J]. Mathematical Proceedings of the Cambridge Philosophical Society，1980(87):151-155.

[6] Belikov V V，Ivanov V D，Kontorovich V K，et al..The non-Sibsonian interpolation.A newmethod of interpolation of the values ofa function on an arbitrary set of points[J].Computational Mathematics and Mathematical Physics，1997(37):9-15.