基于HHT方法的微差爆破延期时间识别与应用

刘金川 方 向 冯伟涛

0 引言

微差干扰降震法良好的降震效果使其成为降低爆破震动强度的最主要手段，已广泛应用于矿山爆破施工中。实现微差爆破的关键在于选取合理的微差延期时间，本文结合江苏连云港核电5号，6号核岛负挖爆破工程实例，采用 HHT方法，对实测微差爆破震动信号进行EMD分解，获得了体现现场实际情况的地震波IMF分量，从而确定微差延期时间，为今后类似工程中雷管段别选取和控制爆破震动的危害效应提供了参考。

H ilbert-Huang Transform(简称HHT)是一种由Norden E Huang等人提出的处理非线性、非平稳信号的被验证有效的最新时频方法，是近年来以Fourier变换为基础的线性和稳态谱分析的一个重大突破。HHT方法已在地震学领域及地震工程领域取得了一些重要成果，并在爆破震动信号的处理方面得到了初步应用。

微差爆破是爆破工程技术中最主要的控制爆炸输出能量的手段。在微差爆破中，每一个段别的雷管起爆相应的就有一次能量的突然加载，同时引起测点的爆破震动信号在时程曲线上的一次突变。本文先对爆破信号进行 EMD分解，获得反映信号信息主要成分的IMF分量，再利用IMF分量的Hilbert变换构造信号，最后画出构造信号的包络幅值曲线，识别、分析出实际微差延期时间。

1 HHT方法

HHT方法分为两个部分即经验模态分解EMD(Empricial Mode Decomposition)和Hilbert谱分析。HHT对于非平稳的信号处处理分为两个部分:首先将任意给定的非平稳信号通过EMD成为一组固有模态函数(Intrinsic Mode Function，IMF)，然后分别对每一个IMF分量进行Hilbert变换得到H ilbert谱，即将该IMF表示在联合的时频域上。最后汇总所有IMF的Hilbert谱，从而得到原始非平稳信号的Hilbert谱，该Hilbert谱是原始非平稳信号能量随时频的分布表示。

1.1 EMD方法得到IMF分量

任何复杂信号都由一些互不相同的、简单的、非正弦函数的IMF分量组成，IMF须满足两个条件:

1)整个数据序列中，极值点的数量与过零点的数量相等或至多相差1;

2)信号上任意一点，由局部极大值点确定的包络线和由局部极小值点确定的包络线的均值均为 0，即信号关于时间轴距对称。

IMF分量可以是线性或非线性;任何时候，一个信号都可以包含多个IMF;如果模态之间有相互重叠，便形成复合信号。Huang等人基于此提出EMD方法，即Huang变换。EMD法是HHT关键，该分解算法也称为筛选过程(the sifing processing)，它具有除去叠加波和使波形更加对称。通过 EMD方法可以将原始信号x(t)分解，依次得到IMF分量c1，c2，…，cn及残差余量rn。

那么原始信号x(t)就可以表示为n个IMF分量及rn的和:

1.2 Hilbert变换提取包络

应用EMD方法可得到多个IMF组合，对IMF分量c(t)进行Hilbert变换:

其中，PV代表柯西主值(Cauchy Principal Value)，因此构造信号z(t):

其中，a(t)为z(t)的幅值，也称为信号x(t)的包络，或调制信号，幅值函数表达式为:

1.3 微差延时识别

通过爆破时域波形的EMD分解，得到多个IMF分量。分析所得分量的时程曲线图，将振速较大、振幅变化明显的IMF确定为爆破震动信号的主成分分量。

对确定的IMF分量作为Hilbert变换，并根据式(4)提取其包络曲线图，明显的包络峰值(包络极值点)即微差爆破各段雷管的起爆时刻，进而得到爆破段数。由于微差爆破中延期时间是前后两段爆破间的时间差，因此选取哪一点作为起始点并不影响微差延期时间的计算，如果将第一个突峰位置作为最低段次雷管的起爆时刻，则可以得到实际微差延期的时间，再将实际的段间延时与设计的延时时间进行比较，即可以较好的识别各段雷管的误差精度，从而真正地把握实际微差延时。

2 工程背景

江苏连云港核电 5号，6号核岛扩建工程采用深孔台阶爆破方法，为保护临近建筑物，特别是减小主控室(21UCB)的精密仪器设备的爆破震动影响，爆破设计采用多段孔内、孔外联合微差延时爆破，共计 8个段别。图1为第 0638次爆破实测信号的垂直(V向)振动时程曲线，爆破条件及爆破参数如表 1所示。

3 基于HHT的微差延时间分析

在Matlab7.1语言的平台上编程，对测试的振动数据进行处理，由上述HHT方法求出原始振动波形的IMF分量、IMF包络幅值，再进行分析处理，得到相应的结果。一般情况下，振动垂直分量较能代表信号的特点，本文选取垂直分量的爆破震动信号为分析对象。

表1 微差爆破的参数

对图1中的爆破震动信号进行EMD分解，得到8个IMF分量(c1～c7)和一个残差余量c8的振速—时间图，由于篇幅有限只画出IMF分量(c1～c4)，如图2所示。

从IMF分量可以看出，第三个IMF分量c3是震动信号的主成分分量，按照式(2)对其进行H ilbert变换，构造解析信号并根据式(4)提取其包络曲线图，如图3所示。

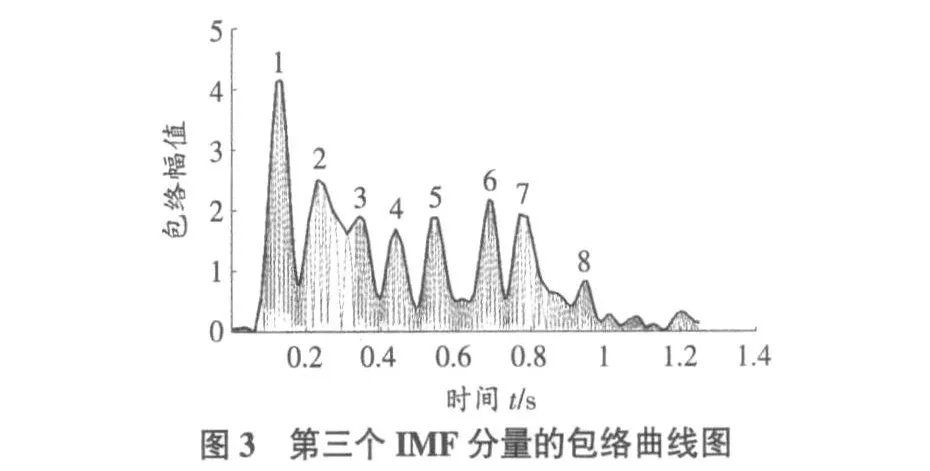
图3中明显的包络峰值即为包络极值点，可以读出图中有 8个突峰及微差爆破各段雷管的起爆时刻，它们分别为 0.129 3 s，0.232 6 s，0.346 1 s，0.442 8 s，0.545 3 s，0.691 6 s，0.772 0 s，0.943 4 s，这表明该爆破震动信号是由 8段微差爆破震动波叠加而成。选取第一个突峰位置作为最低段次雷管的起爆时刻，则实际的微差延期时刻分别为 0 s，0.103 3 s，0.216 8 s，0.313 5 s，0.416 0 s，0.562 3 s，0.642 7 s，0.814 1 s，进而可得段间微差延期时间分别为103ms，113ms，96.7ms，102.5ms，146.3ms，80.4ms，171ms，与实际微差爆破设计延时进行比较，即可较好的识别各段雷管的误差精度，把握微差爆破延时时间，达到更好的削弱爆破输出能量的目的。

4 结语

1)微差爆破延期时间的选取，既可能削弱爆破震动效应，也可能使爆破震动效应加强。因此，合理地选择微差时间可以使地震波的能量在时间和空间上恰好相互错开，避免能量集中，从而有效降低爆破地震强度。

2)利用HHT方法中的EMD能高效分解和细化微差爆破震动信号，能得到各段雷管起爆时刻，计算延时时间，为微差爆破方案设计提供了一定的参考。

[1] 吴腾芳，王 凯.微差爆破技术研究现状[J].爆破，1997，14 (1):53-57.

[2] 张义平，李夕兵，左宇军.爆破振动信号的HHT分析与应用[M].北京:冶金工业出版社，2008:78-80.

[3] Huang N E，Shen Z，Long SR，et al.The empiricalmode decomposition and the H ilbert spectrum fornonlinear and non-stationary time series analysis[J].Pro.Roy.Soc.，1998(454): 903-995.

[4] 胡昌华，李国华，刘 涛，等.基于MATLAB6.X的系统分析与设计——小波分析[M].西安:西安电子科技大学出版社，2000.

[5] 张义平，李夕兵，赵国彦，等.基于HHT方法的硐室大爆破震动分析[J].岩石力学与工程学报，2005，24(1):4784-4789.