基于块矩阵的快速图像分割

谷 莉

同济大学软件学院，上海 201804

1 概述

图像分割在计算机视觉领域中的一个经典问题，图像分割的方法也多种多样。近年来基于图论的分割方法逐渐成为研究热点[1]。基于图论的图像分割方法的基本原理是首先对输入的图像建立一个带权的无向图，其中图的一个顶点代表图像中的一个像素，边上的权表示边上两个顶点之间的相关性，然后定义一个目标函数并对其优化求解，目标函数的最优解对应一种图像分割。

对不同的目标函数会有不同的求解方法。谱分析是一种常用的求解方法。这里的谱分析是指用拉普拉斯矩阵的特征向量分析问题。然而，求矩阵特征向量的过程是非常耗时的，也对计算机内存要求很高，这就在很大程度上限制了这类方法的应用。本文提出了一种基于块矩阵的方法能有效地解决这个问题，它不仅可以加速分割过程，同时还可以处理较大的图像。

2 谱聚类与图像分割

由于聚类问题和图像分割本质上是相同的，所以许多用作谱聚类的标准和方法也可以用来实现图像分割。

2.1 图像分割的度量标准

通常，把图像中的每个像素看作一个节点，可以构造一个带权的无向图T=（V, E, W）。V是所有节点的集合；E是图中所有边的集合；W是权矩阵，矩阵元素w（i, j）表示顶点i和j之间的相关性。将图像一分为二实际上就是将顶点集合V分成两个不相交的子集A和B ：且。那么衡量图像分割结果好坏的标准可以用下面的等式来定义：

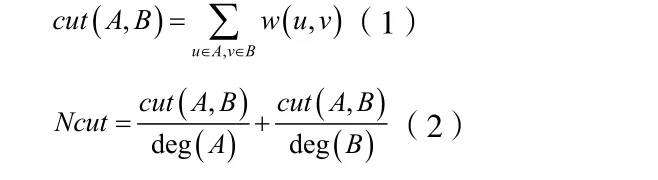
2.2 求解目标函数的谱方法

事实上，这个最小化问题可以转化为广义特征值问题[1]：

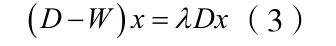
权矩阵W 中元素w（i,j）表示顶点i和j之间的相关性；权w（i,j）越大表示顶点i和j之间的相关性越强，分在同一个子集中的可能性越大。由于图像一般只是局部相关的，可以将顶点距离大于r（r远小于像素个数）的那些顶点之间的权w（i,j）赋值为0，这样对计算得到的Fiedler向量的分量排序没有太大影响，同时由于权矩阵W变成了稀疏对称矩阵还可以加快计算速度。

3 基于块矩阵的图像分割

然而求解特征值方程（3）的全部特征向量是既耗时又耗费内存的工作，它的运算数量级是O（n3）。在处理大图像时,这是很不实际的。但是用Fiedler向量分割图像具有下列特性：

1）图像在多数情况下仅仅是局部相关的，所以最后得到的权矩阵W是稀疏矩阵；

2）对Fiedler向量的精确度要求不高，图像分割中实际使用的是其分量的排列顺序。

针对这些特性，我们提出块矩阵方法来快速求解近似的Fiedler向量。可以从图像分块的角度来理解矩阵分块的思想。首先将一幅图像m分成4块（也可以更多）mi，i=1...4。对每个块图像分别求其权矩阵Wi,i=1...4，他们正好对应主对角线上的块矩阵。由于图像分块产生的边界打断了原图像m的连续性，所以需要在局部区域附加一些约束以保持其原有的连续性。这里我们是在块与块之间的边界周围扩展了部分区域形成一些小的块图像，n12…n5就是由边界扩展生成的块图像。这些扩展块的大小通常可以规定为边界两边各2r个像素的范围内。在扩展块图像中边界线两侧像素之间的相关性形成的权矩阵正好对应非对角线上的块矩阵。

3.1 算法步骤

综上所述，基于块矩阵的分割方法可以通过如下步骤实现：

1）将图像分成几大块，分别计算其Fiedler向量并形成块图像的（局部）分割，然后将这些局部分割综合起来形成整幅图像的初始分割；

2）在边界周围扩展生成块图像，分别计算其Fiedler向量并形成局部分割，用这些局部分割结果来优化初始分割中边界附近的分割。

4 实验结果分析

用本文提出的基于块矩阵的方法分割场景图像好处是：1）对同样大小的图像，我们可以得到与Ncut方法[1]相似的分割结果（图1），同时还能大大提高分割速度；2）由于Ncut方法计算过程占用大量的计算机内存,对一些较大的图像用它根本无法分割，而用本文提出的方法可以很容易地完成分割并得到理想的结果。

图1

图1一幅160X160的婴儿图像。a∶Ncut方法的分割结果，整个过程花费了35.16秒；b：用本文提出的方法分割得到的结果，整个过程只需要20.79秒。

5 结论

本文提出一种新的快速图像分割方法，和其它谱聚类方法相比，本文提出的基于块矩阵的方法在得到很好的分割结果的同时还能大大提高分割速度。

[1]J.Shi and J.Malik.Normalized cuts and image segmentation [J].IEEE Trans. on Pattern Anal.and Machine Intell.2000，22(8)：888-905.