基于ANP方法的公交车实时调度策略选择研究*
2011-04-10孙传姣
孙传姣 王 磊 刘 飞
(交通运输部公路科学研究院 北京 100088)
公交实时调度策略就是利用先进的技术手段,动态地获取实时交通信息,实现对车辆的实时监控和调度,使其能够科学合理地运行,从而改善公交服务水平,提高乘客乘车的舒适度[1].实时调度策略的方法有很多种,本文重点考虑滞站调度、跳站调度、短掉头和发车调度4种调度策略[2-5].
为了正确评价在公交实时调度策略选择中的因素,需要确定影响策略选择的因素,确定的指标从乘客和公交公司两方面考虑.在影响乘客的出行方面,有出行的时间、出行的费用、出行的方便性、舒适性等;影响公交公司的因素,主要包括实时调度策略的实时是否会影响运行的时间和效益,是否需要对司售人员进行培训,在实施方案的时候是否需要投入大量的成本,配置有关的配套设施,以及方案实施的难易程度[6-8].
1 ANP的建模方法
采用网络分析法(ANP)分析问题的步骤主要包含.
步骤1 问题描述,依据目标、准则构建网络
首先对决策问题进行详细的描述,包括该决策问题的目标、准则以及子目标.基于目标、网络构建ANP网络.典型ANP网络如图1所示,它由两部分构成:一部分是控制层或者称为目标、准则层;另一部分是网络层,网络层是依据控制层的准则而建立的,并且反映了在相应目标、准则下网内的元素或元素组是如何相互影响的.这体现ANP与AHP在结构形式上的差异.此外,ANP可以依据各个准则,分别构建子网,每个子网由反映相应控制准则的元素组构成.
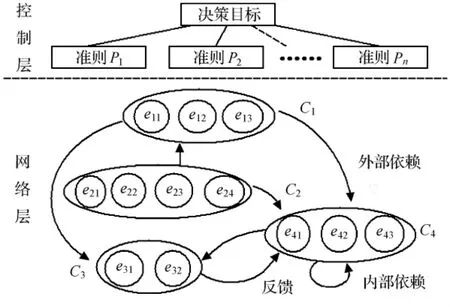
图1 ANP网络
步骤2 确定两两比较方法,构建无权重超矩阵 构建无权重超矩阵Ws,即应用两种比较方法对元素进行两两比较.在构建的过程中,首先以该网络中某一元素组Cj中的元素ejl(l=1,2,…,nj)作为准则,按照元素ejl对元素组Ci中各元素的影响程度或按照元素组Ci中各元素对元素ejl的影响程度构造判断矩阵.
依次将Cj中的各元素作为准则,将元素组Ci与元素组Cj中的元素两两比较,构造各自的判断矩阵,最后将各判断矩阵的归一化特征向量汇总到一个矩阵Wij中,最终可获得无权重超矩阵Ws,该矩阵表示元素组Ci中的元素与元素组Cj中的元素之间的影响关系.
步骤3 构建权重超矩阵,求得极限超矩阵
依据给定准则对元素组进行成对比较,可获得在某一准则下反映元素组间关系的权重矩阵As,有了该权重矩阵,就可以获得权重超矩阵,即以权重矩阵As乘以无权重超矩阵Ws得到权重超矩阵Wws.对权重超矩阵进行归一化处理,得到极限超矩阵Wls.由于元素间存在依存与反馈关系,因而归一化的过程是一个反复迭代、趋稳的过程.
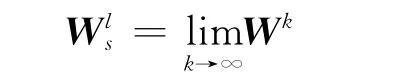
步骤4 极限相对优先权的综合,可选方案排序
对每一控制准则的极限向量按照各准则权重加总,主要是对各可选方案的权重加总.依据各可选方案的权重值排序.
2 基于ANP的方法调度策略选择
某城市欲在公交走廊上实施实时调度策略,其具体情况如下:走廊内最大高峰小时客流量为12 128人次,平均10 162人次,客流巨大,特别在早晚高峰的时候需要有针对性进行实时调度,此公交线路共设置站点20个,线路共有配车40辆.根据走廊的情况,高峰小时给出了具体的4种不同的调度策略,见表1.

表1 调度策略实施方案的比较
为了合理评价出合理的调度策略,采用ANP建模分析的方法对其进行分析.主要步骤如下.
1)描述目标,建立网络,如图2.此图为在ANP方法的软件Super Decision中建立的公交系统的网络图,其中的双箭头表示两组之间有联系,而圆弧表示在同组的元素之间有联系.

图2 公交实时调度策略评价的ANP网图
2)确定两两比较方法,构建无权重超矩阵.所有有相互关系的元素需要进行两两比较,原则是相对于准则两者的重要程度,用1~9之间的数字表示出来.表2给出方案一在族“经济因素”之间的重要程度比较.

表2 元素之间的关系表
表2第二行第四个单元格的数值1/5表示:对动态跳站调度策略而言,影响乘客的因素方面出行时间比出行习惯的改变重要,说明这种策略更关注的出行时间的节省.按照上面的方法,依次可以构造多个判断矩阵.将判断矩阵进行组合组成无权重超矩阵如表3所列.
3)构建权重超矩阵,求得极限超矩阵 在获得无权重超矩阵后对各元素组进行组间比较,对元素组进行两两比较.考虑到线路的实际情况,以及公交提供的服务重点是对于乘客的影响因素,因此在进行元素比较的时候,乘客的因素更为重要,表3显示对于方案选择而言,各组因素间的比较,得到一个判断矩阵如表4所列.

表3 无权重超矩阵

表4 组之间的关系表
如此,依各准则进行元素组之间的比较,并将获得的各判断矩阵归一化,然后合并,再与无权重矩阵相乘,即可获得权重超矩阵,对权重超矩阵进行归一化最终获得如表5的极限超矩阵.
4)极限相对优先权的综合,可选方案排序对得到的优先权重值进行归一化处理,得到图3的决策优先权.
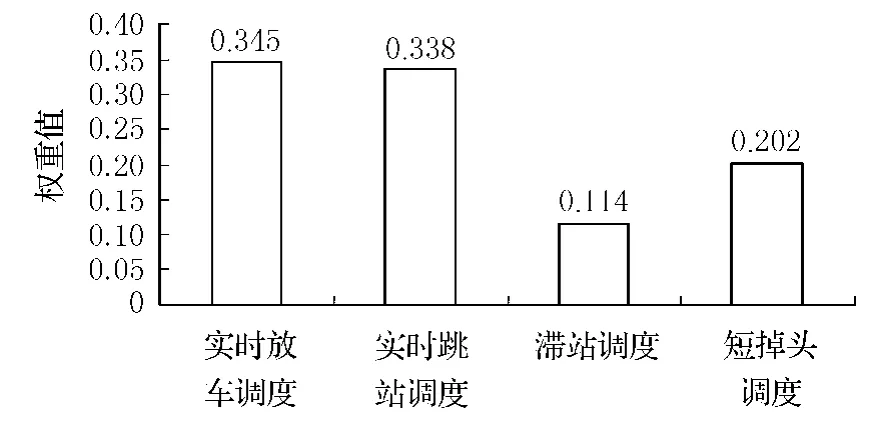
图3 优先权重值
通过ANP方法将调度方案选择问题描述为一个具有依存、反馈关系的网络,该方法与AHP方法相比更接近现实情况,能提高可选方案优先权的精确度,减少因AHP局限性带来的排序误差大、甚至排序颠倒的现象,最终使得调度方案的选择更为科学.由图3可以看出,在给定的情形下,四种策略中的实时放车调度和跳站调度的优先权重值比较高,是需要优先考虑的调度方式.短掉头调度其次,滞站调度的效果不够明显.
3 结束语
本文利用ANP方法对公交实时调度策略选择进行了评价,给出了四种不同的实时调度策略,分别为滞站调度、跳站调度、短掉头和发车调度,为了评价四种策略的适应性,本文引入ANP方法对策略进行评价,选择了影响乘客因素和影响公交公司的12个方面的相互影响因素,基于网络分析法进行了方案的优化选择.在给定的情形下,四种策略中的实时放车调度和跳站调度的优先权重值比较高,是需要优先考虑的调度方式.短掉头调度其次,滞站调度的效果不够明显.

表5 极限超矩阵
[1]于 滨.城市公交系统模型与算法研究[D].大连:大连理工大学交通学院,2006.
[2]牛学勤,陈 茜,王 炜.城市交通线路调度发车频率优化模型[J].交通运输工程学报,2003,3(4):68-72.
[3]陈云新,谭汉松.公交车线路运营调度及评估系统的研究与实现[J].武汉理工大学学报.2005,27(9):97-100.
[4]宋 瑞,赵 航.基于机会约束的公交调度研究[J].数学的实践与认识.2005,35(1):89-95.
[5]戴连贵,刘正东.公交调度发车间隔多目标组合优化模型[J].交通运输系统工程与信息.2007,7(4):43-46.
[6]邹 迎.公交区域调度行车计划编制方法.交通运输系统工程与信息[J].2007,7(3):78-82.
[7]耿金花,高圣齐.序贯均匀设计在公交优化调度问题中的应用[J].青岛科技大学学报,2007,28(3):263-266.
[8]周雪梅,杨晓光.基于ITS的公共交通换乘等待时间最短调度问题研究[J].中国公路学报,2004,17(2):82-84.
