卡尔多炉弹性元件动力学仿真

张廷波

ZHANG Ting-bo

（甘肃省机械科学研究院，兰州 730030）

0 引言

卡尔多炉（kaldo），又称氧气斜吹转炉，1956年由卡林(B.Kalling)试验成功，并在多姆纳维特厂(Domnavet)投产，是一个衬有耐火砖的钢制容器，由炉身、弹性元件、摩擦圈、支撑轮、底座等零部件构成。工作时，炉身呈倾斜状置于摩擦圈上，在电机的驱动下，以15 r/min左右的速度绕与水平成28o夹角的旋转轴旋转。炉身和物料重量通过预紧弹性元件传递到摩擦圈上，再传递到底座。卡尔多炉作为世界上最先进的冶炼设备之一，具有原料适应性强、综合回收率高，炉内温度易控制，能耗低、生产效率高等优点，在冶炼行业得到广泛应用。

目前，国内对卡尔多炉的研究仅限于工艺和控制领域，对其结构和力学性能的研究分析很少，但动力学分析对卡尔多至关重要，通过动力学分析可以了解各个零部件在工作状况下的受力情况。本文主要研究弹性元件的力学特性及其在卡尔多炉工作状态下的受力情况，并讨论其强度问题。弹性元件作为卡尔多炉的关键零件，承受着整个炉身和物料的重量，了解其受力情况及其重要，直接关系到卡尔多炉能否正常工作。

1 弹性元件力学特性

卡尔多炉弹性元件分为径向弹性元件和轴向弹性元件。纵向和横向弹性元件分别由108根和60根φ70的60Si2MnA弹簧钢丝及其附件构成。钢丝在加工过程中存在加工误差，误差在(-0.5，0.5)mm之间。加工误差使得每根钢丝长度不一致，造成钢丝受力不均匀，从而使得在材料线弹性范围内，弹性元件的力学性能表现出非线性。

假设弹性元件钢丝长度x服从正态分布，则x的概率密度函数为

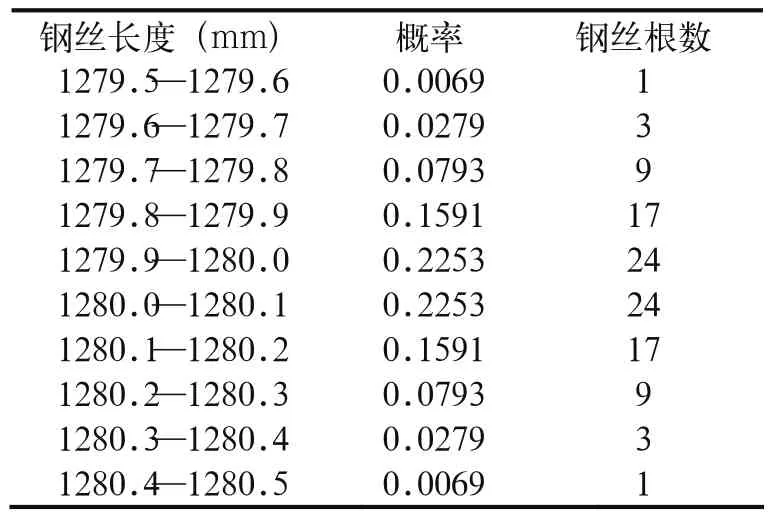
表1 径向弹性元件钢丝长度概率分布

根据已知钢丝长度分布，应用有限元软件ANSYS模拟弹性元件受力过程。将弹性元件一端固定，另一端施加拉力，从而得到弹性元件受力与钢丝位移的关系如图1、图2所示，其中弹簧钢60Si2MnA的力学性能如表2所示。

表2 60Si2MnA弹簧钢力学性能

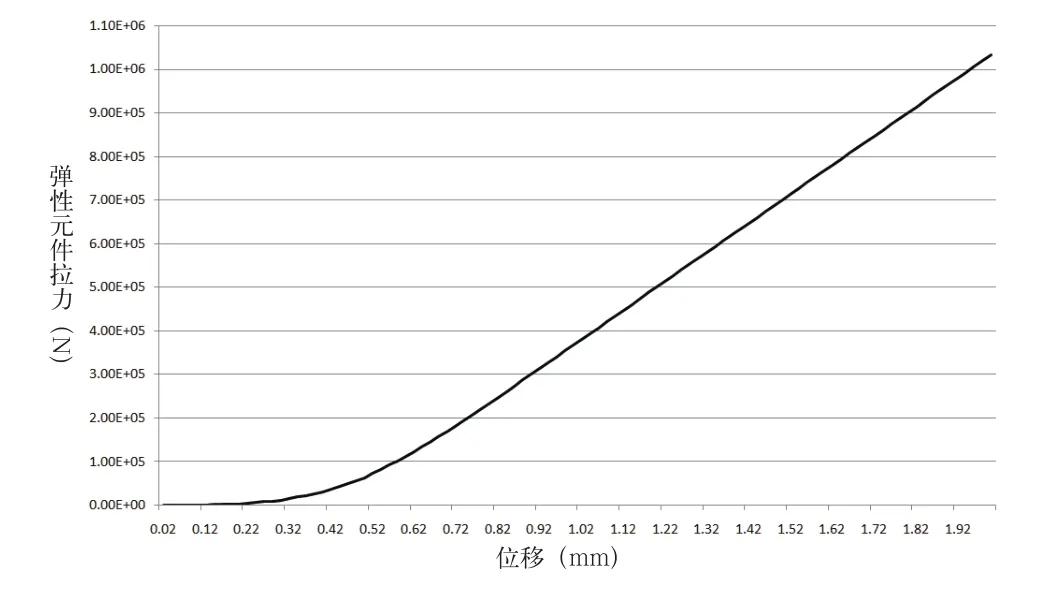
图1 径向弹性元件受力与位移关系

图2 轴向弹性元件受力与位移关系

由图1、图2可见，当弹性元件受力小于100KN时，弹性元件部分钢丝受力，力与位移非线性关系明显；当弹性元件受力大于100KN后，非线性效果较小，工程中可作为线性来处理；随着弹性元件受力增大，所有钢丝开始受力，此时弹性元件完全处于线性状态下。在卡尔多炉工作状态下，径向和轴向弹性元件的预紧力分别为560KN和320KN，由图1、图2可见，此时弹性元件力学性能在线性区内。因此，钢丝加工误差对弹性元件正常工作的影响很小，可忽略不计。

2 工作状态下弹性元件受力分析

卡尔多炉工作时，炉身呈倾斜状置于摩擦圈上，在电机的驱动下绕与水平成28o夹角的旋转轴旋转。炉身分别通过16个纵向和轴向预紧弹性元件将重力传递到摩擦圈上。弹性元件在实际工作中只受拉力且纵横比大，弹簧钢丝间没有相互作用，故可把108根和60根弹簧钢丝等效成等截面面积圆柱来模拟弹性元件，其预紧力大小如表3所示。

表3 弹性元件上施加的预紧力值

弹性元件在卡尔多炉旋转过程中拉力不断变化，要了解其受力情况，需进行动力学分析。下面通过有限元软件ANSYS中的Workbench平台对卡尔多炉进行瞬态动力学仿真。瞬态动力学分析能够得出任何结构关于时间载荷的响应，动力学运动方程：

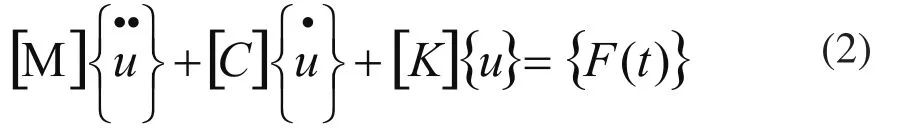
其中，[M]为质量矩阵，[C]为阻尼矩阵，[K]为刚度矩阵，F(t)为力载荷向量。

Ansys Workbench瞬态动力学分析提供了三种求解方法：完全法、缩减法和模态叠加法。完全法使用了完全的系统矩阵来计算系统响应，而没有简化矩阵；模态叠加法是确定结构的固有频率和模态，乘以正则化坐标，然后加起来计算节点的位移解；缩减法是通过采用计算主自由度和简化矩阵来压缩问题。由于仿真中涉及到接触问题，因此本文采用完全法。

Ansys Workbench中的瞬态动力学模型既可以是刚体，也可以是柔体。在动力学分析中，时间步长是一个很重要的概念，它决定了求解精度。在本次仿真中采用自动时间步长，当输入程序将依据自动时间步长算法而决定最优的值。

卡尔多炉实际结构复杂，根据分析目的对模型进行简化，仅保留摩擦圈、弹性元件和炉身，物料重量通过施加力的方式添加。因主要分析弹性元件受力情况，故将摩擦圈与炉身设为刚体，仅对弹性元件进行六面体网格划分，仿真模型如图3所示。

图3 卡尔多炉动力学仿真模型

在仿真分析中，弹性元件和炉身之间及弹性元件和摩擦圈之间建立绑定接触；在卡尔多炉仿真模型上建立局部圆柱坐标系，坐标系Z轴与卡尔多炉旋转轴重合。在局部圆柱坐标系中，约束摩擦圈轴向自由度，使得摩擦圈只能绕旋转轴旋转，考虑重力影响，其中炉身与物料总重量为300t。在炉身上施加如图4所示的旋转角速度，其中在0～1s内，先对弹性元件施加预紧力；再在1～2s内施加炉身与物料总重量；2s后炉身开始旋转。

图4 炉身上施加的旋转角速度随时间变化关系

在仿真过程中，选取如图5所示的上、下径向和轴向4个弹性元件，监测随炉身旋转弹性元件拉力变化情况；选取炉身顶部旋转轴上一点，监测随炉身旋转该点的位移变化情况，图6、图7分别为弹性元件拉力随时间变化关系曲线和监测点竖向位移随时间变化关系曲线。

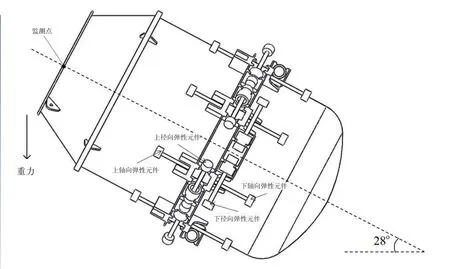
图5 卡尔多炉示意图

图6 弹性元件预紧力随时间变化关系

图7 监测点竖向位移随时间变化关系

由图6可见，在初始阶段，弹性元件拉力保持预紧力大小，随着炉身与物料重量的施加，上径向弹性元件和上轴向弹性元件拉力增大，下径向弹性元件和下轴向弹性元件拉力减小，并伴有微小振荡。当2s后炉身开始旋转，弹性元件拉力呈正弦变化，其中上径向弹性元件的受力范围为250—910KN；下径向弹性元件的受力范围为210—920KN；上轴向弹性元件的受力范围为360—620KN；下轴向弹性元件的受力范围为200—420KN。对于纵向弹性元件，当其轴线与竖直平面平行时受力最大；对于下横向弹性元件，旋转到炉顶时受力最小，旋转到炉底时受力最大；对于上横向弹性元件，旋转到炉顶时受力最大，旋转到炉底时受力最小。

图7表明，在弹性元件预紧阶段，炉身基本保持静止，没有位移运动；随着炉身与物料重量的施加，炉身顶部开始沿竖直向下方向运动，并伴有微小振荡。炉身开始旋转后，监测点竖向位移随时间呈正弦变化，变化范围为（-0.7—0.6）mm，此变化范围符合设计要求。

根据监测得到的弹性元件拉力值，可以求得其上最大轴向应力如表4所示，可见应力值小于材料屈服强度，不会发生强度破坏。

表4 弹性元件最大轴向应力值

3 结论

本文通过仿真分析研究了钢丝加工误差对弹性元件力学性能的影响，结果表明在弹性元件初始受力阶段力与位移为非线性关系，但弹性元件工作拉力在线性段，故加工误差对弹性元件正常工作影响很小；在卡尔多正常运行过程中，预紧弹性元件受力大小随炉身旋转位置不同而呈周期性变化，弹性元件应力值小于材料屈服强度，不会发生强度破坏。本文得到的仿真结果对卡尔多炉的设计具有参考价值和指导意义。

[1] 段志良,马英奕.卡尔多炉PCS7过程控制系统合并优化[J].铜业工程,2011-05(2)：45-51.

[2] 欧阳晖,汪荣彪.卡尔多炉处理废杂铜技术[J].铜业工程,2009(3)：37-39.

[3] 刘金庭.卡尔多炉炼铅主体设备的转化设计[J].有色设备,2007(1)：23-26.

[4] 李志刚,何醒民.卡尔多炉炼铅工艺在我国的首次引进应用[J].工程设计与研究,2006,12.(121)：14-16.

[5] 有色冶金炉设计手册编委会.有色冶金炉设计手册[M].冶金工业出版社,2000.

[6] 庄茁(译).连续体和结构的非线性有限元[M].清华大学出版社,2003.

[7] 浦广益.ANSYS Workbench 12基础教程与实例详解[M].中国水利水电出版社.2010.

[8] 成大先.机械设计手册第四版第一卷[M].化学工业出版社.2003.

[9] 张策.机械动力学[M].高等教育出版社,2008.

[10]Manuel Perez-Tello,Víctor M.Sanchez-Corrales,Moises R.Prieto-Sanchez,et al.A kinetic.model for the oxidation of selenium and tellurium in an industrial kaldo furnace[J].JOM Journal of the MineralsMetals and Materials Society,2004,Volume 56,Number 12,Pages 52-54.