一类含立方项非线性振动微分方程的解析解

何松林

(昆明学院物理科学与技术系，云南昆明650214)

0 前言

含立方项的非线性振动是物理学及工程应用中出现较多的一类非线性振动［1－2］。立方项系数远小于线性项系数的杜芬方程，作为弱非线性的典型代表，得到了非常广泛的应用［3］。近年来，有关含立方项的强非线性实际振动系统的研究越来越多，如双弹簧振子的横向振动［4］、新材料中的纳米机械共振子的振动［5］及悬索的振动［6］等。描述这些振动系统的微分方程中，线性项常常小于立方项，甚至仅存在立方项。为了解决强非线性振动在工程设计中的实际应用，出现了诸如能量法、广义谐波函数平均法、范式理论方法、同伦摄动法及迭代摄动法等多种强非线性振动系统周期解的近似求解方法［7－12］。这些方法原则上都可以用来求解强立方非线性振动方程周期解，但只能得到近似结果。本文将依据弹性力作用下系统机械能守恒的原理，求解出一类含有线性项和立方项的非线性微分方程的精确解析解。

1 含立方项非线性方程的椭圆函数解

常见的含立方项非线性自由振动微分方程可表示为:

式中，k1≥0，k2≥0是由振动系统性质决定的非负常数。为了方便，设初始条件为:

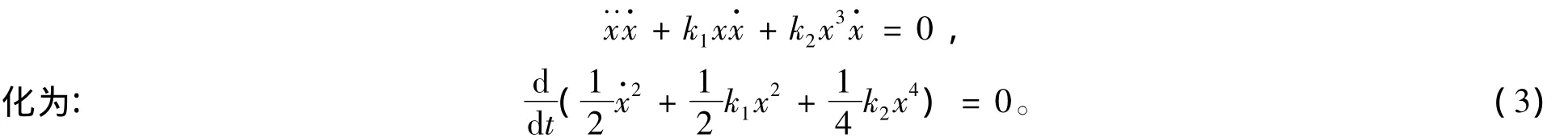
式(3)表明:方程(1)表示的系统在振动过程中总机械能守恒。设总机械能为E，则在式(2)表示的初始条件下E=k1A2+k2A4，从而:

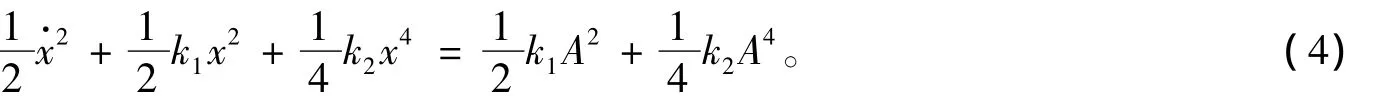
式(4)表明:系统的相图为闭合凸曲线，则式(1)的解可设为［9］:

将式(5)求导得:

将式(5)、式(6)代入式(3)得:

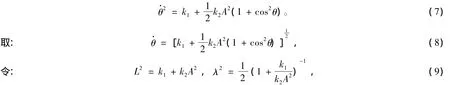
则式(8)化为:

式(10)两端积分得:

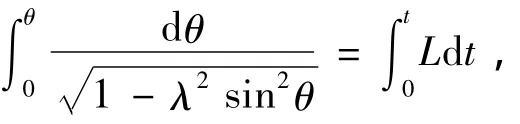
即:

其中，F(θ，λ)是模为λ，参数为θ的勒让德第一类椭圆积分［13］，其反函数为:

将式(12)代入式(5)得:

相应地:

式(13)、式(14)中sn、cn和dn是雅可比椭圆函数。椭圆函数是双周期的亚纯函数，椭圆余弦函数cn的一个实周期为4K(λ)=4F(，λ)，其中，K(λ)是模为λ的第一类完全椭圆积分。因此，由LT= 4K(λ)可以得到式(1)表示的振动系统的周期为:

2 具体算例

为了考察方程(1)的解析解式(13)的合理性，具体分析几个算例。

2.1 线性谐振子

当k2=0时，式(1)化为:

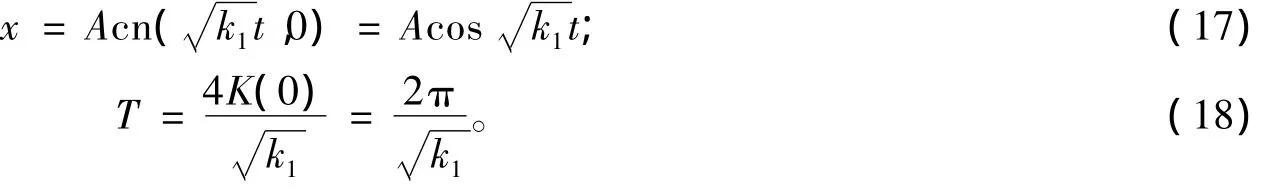
式(17)和式(18)与众所周知的结果完全相同。

2.2 立方非线性振动

当k1=0时，式(1)化为:

式(21)表明立方振子的周期与振幅成反比，比例系数由k2确定。这与已有的报道［14］完全相同。

2.3 杜芬系统的自由振动

当k1=ω;k2=εω，其中0≤ε＜＜1，方程(1)化为:

式(22)是杜芬系统自由振动微分方程，可采用多种近似方法进行求解［3］。

由式(9)得:

将L和λ的结果代入式(13)即可得到式(22)的解。

由于0≤ε＜＜1，而A有限，因而一般有0＜εA2＜1。第一类完全椭圆积分的级数展开式为:

将其代入式(15)，并忽略ε2以上的高阶小量，得:

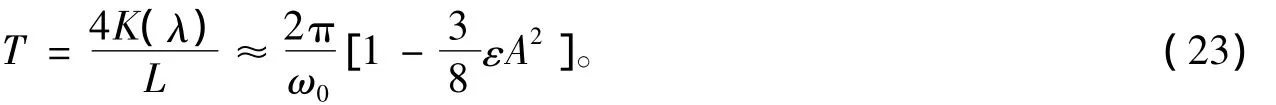
式(23)与采用多种近似计算得到的结果一致［3］。从以上3个算例可以看出:解析解和周期表达式(13)和式(15)是合理的。

3 解析解与数值解结果的比较

将方程(1)采用MATLAB［15］的ode45函数进行四阶龙格－库塔数值求解，将得到的振动曲线与由式(12)计算得到的振动曲线在同一图中进行比较;同时，将数值解得到的相图与由式(12)、式(13)得到的相图在同一图中进行比较。

3.1 程序设计

用fun31.m文件定义待求函数。

在ww1.m文件中实现解析解和数值解结果的比较。

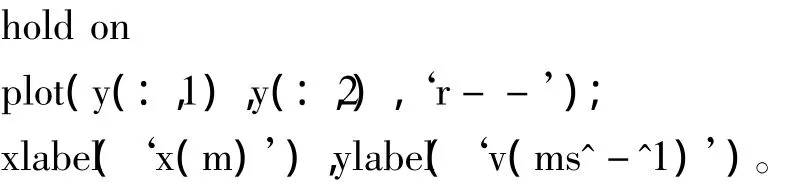
3.2 数值实验结果

采用以上程序进行数值实验发现:无论k1、k2和A如何取值，由式(13)和式(14)得到的振动曲线和相图与数值解得到的振动曲线和相图完全重合。

图1是k1=1 s－2，k2=1 m－2s－2，A=1 m时方程(1)的数值解(虚线)与解析解(实线)结果的比较。图1a是振动曲线的比较，t是时间，x是位移。图1b是相图的比较，其中，x表示位移，v表示速度。由图1可见:无论是振动曲线还是相图，解析解与数值解的曲线完全重合。这充分说明椭圆函数型解式(13)和式(14)式确实有效。

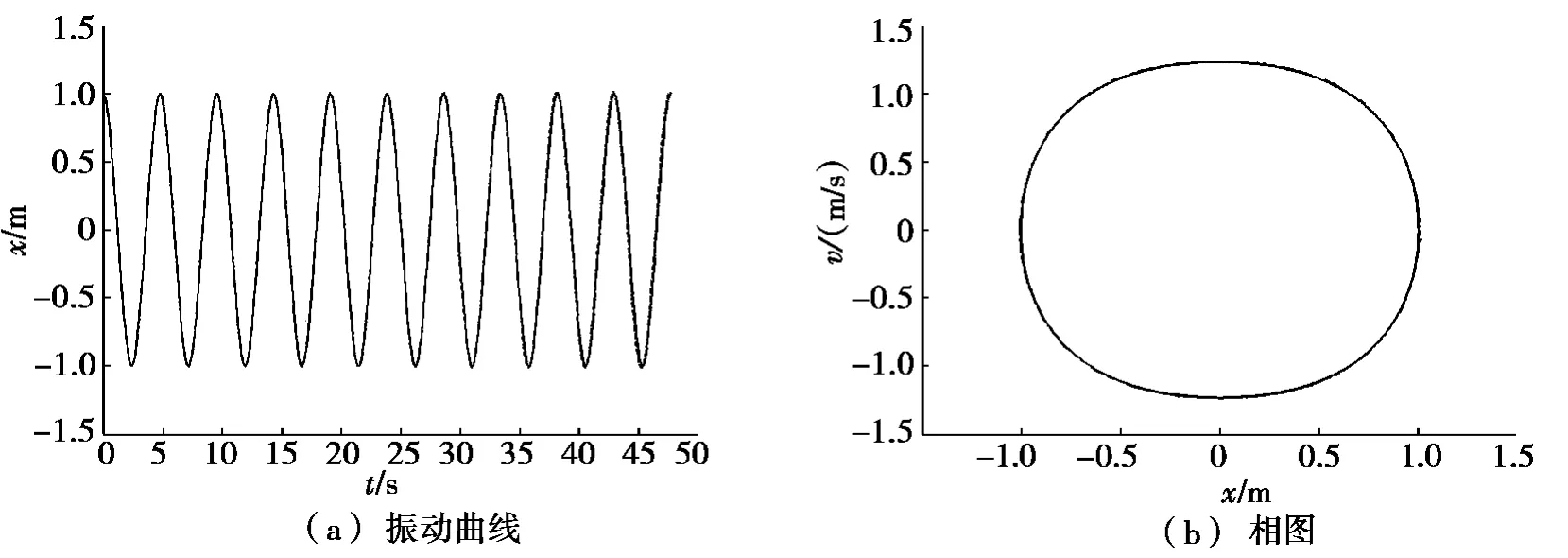
图1 解析解结果(实线)与数值解结果(虚线)比较

综上所述，本文利用仅受弹性力作用的系统，其机械能守恒的原理，精确求解了一类含线性项和立方项的非线性振动微分方程，并通过与常见的算例及一般情况下的数值解结果进行对比，说明解析解是有效的，丰富了含立方项非线性振动的研究。

［1］ 席德勋，席沁.非线性物理学［M］.南京:南京大学出版社，2007:65－74.

［2］ Tomasz K.面向工程的混沌学［M］.施引，译.北京:国防工业出版社，2008:1－5.

［3］ 刘延柱，陈立群.非线性振动［M］.北京:高等教育出版社，2001:8－109.

［4］ 何松林，黄焱，戴祖诚.对称双弹簧振子横向振动的复杂性研究［J］.昆明学院学报，2010，32(3):86－88.

［5］ Karabalin R B，Cross M C，Roukes M L.Nonlinear Dynamics and Chaos in Two Coupled Nanomechanical Resonators［J］.Physical Review B，2008，79(16):1－5.

［6］ Chen Shengming，Chen Zili，Luo Yingshe.Non-Linear Dynamics Analysis of in-plane Motion for Suspended Cable Under Concentrated Load［J］.JCent South Univ Technol，2008，15(s1):192－196.

［7］ Yuriy A R，Marina V S.New Approach for the Analysis of Damped Vibration of Fractionl Oscilltors［J］.Shock and Vibration，2009(16):365－387.

［8］ 丁强生，蒋威，朱小进.一类二阶强迫非线性FDE解的振动性和渐近性［J］.河南科技大学学报:自然科学版，2011，32(4):74－78.

［9］ 李骊，叶红玲.强非线性系统周期解的能量法［M］.北京:科学出版社，2008:1－39.

［10］ 徐兆，詹杰民.强非线性振子的受迫振动［J］.中山大学学报:自然科学版，1995，34(2):1－6.

［11］ 王永岗，宋慧芳，胥掌世.双层旋转扁壳非线性振动分析的同伦摄动法［J］.清华大学学报:自然科学版，2007，47 (8):1389－1392.

［12］ He JH.Some Asymptotic Methods for Strongly Nonlinear Equations［J］.Int JMod Phys B，2006，20:1141－1199.

［13］ 叶其孝，沈永欢.实用数学手册［M］.2版.北京:科学出版社，2006:696－703.

［14］ 佘守宪.X3振荡器的周期运动［J］.大学物理，2000，19(1):19－20.

［15］ 刘惠颖.MATLAB R2007基础教程［M］.北京:清华大学出版社，2008:112－117.