内爆炸载荷作用下爆炸容器振动响应试验研究

2011-03-30年岗顾晓辉成凤生曾星星

装备环境工程 2011年5期

年岗，顾晓辉，成凤生，曾星星

（南京理工大学，南京 210094）

民用设施中的地下隧道、人防工程以及国防领域中弹药洞库、装备存储仓库和危险品储存装置等都可以视为或者近似地视为密闭结构[1—2]。这些密闭结构具有天然抗冲击力强、易于伪装隐蔽以及相对封闭的环境等特点，因而被广泛地应用，但同时也是战时敌方军事打击的重点。精确制导武器和深钻地武器的运用使密闭结构发生内爆成为可能,其自身的生存能力面临着严峻的挑战。与开敞环境不同,密闭结构是一个相对封闭的系统,有明显的“封闭效应”，这一类结构一旦发生内部爆炸，内爆炸载荷会引起结构强烈的动力响应，造成重大人员伤亡和财产损失[3]。因此，研究具有密闭结构的装备、建筑物或地下工事在内爆载荷作用下的冲击振动响应，评估和预测结构的破坏程度，具有很重要的实用价值。

密闭结构在内爆炸载荷作用下的冲击振动响应涉及多学科，理论研究较为困难，原尺寸试验又耗资巨大、费时费力。因此，笔者通过某一尺寸爆炸容器冲击振动环境试验，构建内爆炸振源模型和密闭结构响应模型，监测容器结构外表面4个典型位置的振动情况，分析容器壳体在不同强度载荷下的振动规律和频率特性，提出了判断密闭结构损伤以及如何减少和防止共振响应的方法，并对振动加速度数据进行拟合，弄清其在结构上的衰减规律以及与装药量和爆心距之间的关系[4－5]。

1 内爆炸冲击振动试验

1.1 试验模型设置

将卧式平板封头圆柱形爆炸容器作为密闭结构振动响应模型，其结构如图1所示。其壳体材料为20号钢，壳体长0.8m、内径0.8m、壁厚12mm、封头厚度20mm。容器为轴对称结构，两端的平板封头直接与壳体焊接相连，并在壳体外侧的焊接处加有24块三角形筋板。此外，由于试验的需要，壳体上还开有装药孔、传感器孔、观察孔和清扫孔，试验时所有孔都用相对应的法兰结构进行密闭。

装药选用柱形钝化黑索金作为内爆炸振源模型，从装药孔悬挂放置于容器的中心位置，并由电雷管起爆。

测点布置如图1所示：在容器外侧中环面设置测点A，距其0.3m处同一水平线上设置测点C，同时在顶端距中环面0.1m处设置测点D，在平板封头中心设置测点B。

测试系统如图2所示，主要由加速度传感器、内嵌式数据记录仪及计算机等组成。根据试验经验，加速度传感器采样频率设为250 kHz。传感器使用专用的螺栓固定在相应测点上，在受到内爆炸载荷作用后，壳体表面产生振动并依靠传感器内部的压电特性产生一个与振动加速度成正比的输出电荷量，并经内嵌式数据记录仪中的电荷放大器放大转换为电压信号，再经数据采集系统采集存储，即可得到相应的加速度信号随时间变化的曲线。

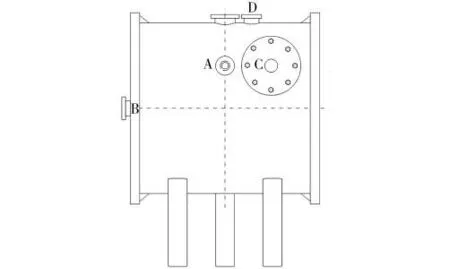
图1 容器结构与测点布局Fig.1 Explosion vesselstructureandmeasuring point location

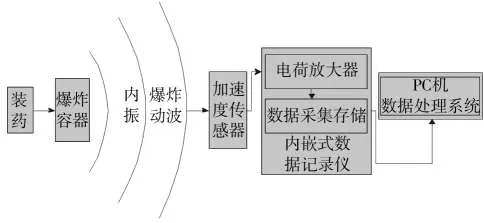
图2 测试系统示意Fig.2 Sketch of the textsystem

1.2 试验结果

内爆炸冲击振动试验在不同药量下共进行了12次：3.6 g下做了3次；6.8 g下做了2次；5 g和10 g下各做了4次。图3为各测点在4种药量下的振动加速度波形。

表1—表4列出了各测点在4种药量下的平均加速度峰值a、爆心距Rw、比例加速度aQ1/3C-2和比例距离值RwQ-1/3。

1.3 结果分析

试验中，同一测点在同一药量下的加速度峰值也有不同，主要是由于每次装药量的细微差异以及装药位置的偏差，这些都会引起载荷分布的不均匀，导致振动加速度产生差异。

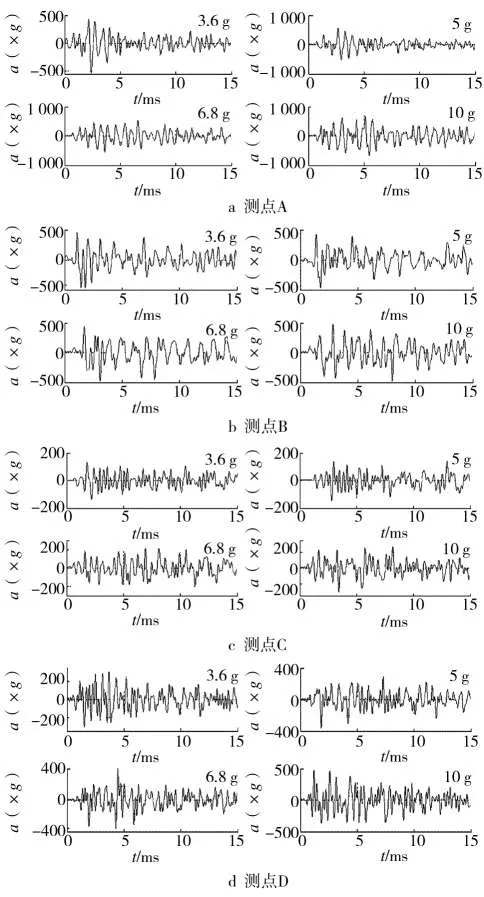
图3 振动加速度波形Fig.3 The acceleration profile

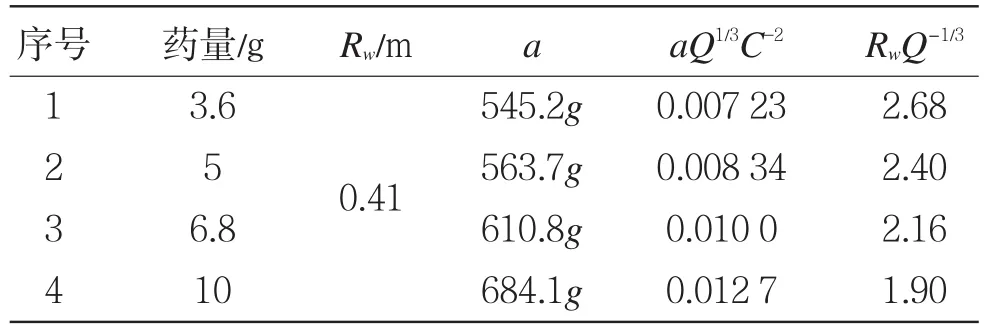
表1 测点A振动加速度实测数据Table1 Experimentaldataofmeasuring pointA

由表1—表4中数据可知，加速度峰值将随着试验药量的增大（或爆心距Rw的减小）而增大，但这种增长并非是线形的，相互之间具体存在何种关系，能否建立相应的计算关系式，将在下一节进行讨论。

振动加速度信号属于非周期平稳信号，选择FFT算法对其进行频谱分析。图4所示为各测点在4种药量下的加速度频谱。

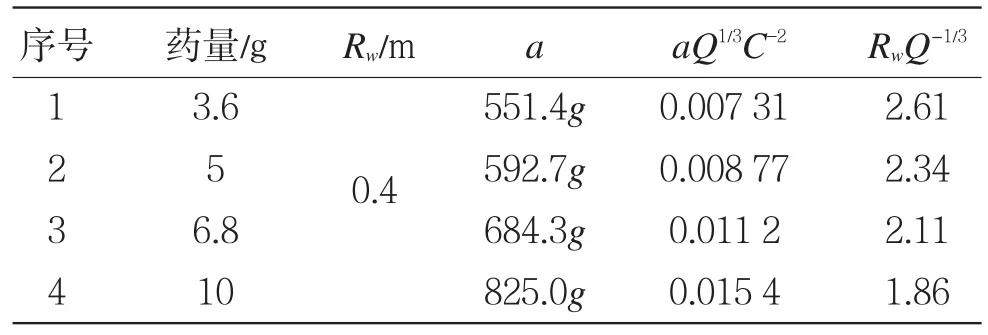
表2 测点B振动加速度实测数据Table 2 Experimentaldata ofmeasuring pointB

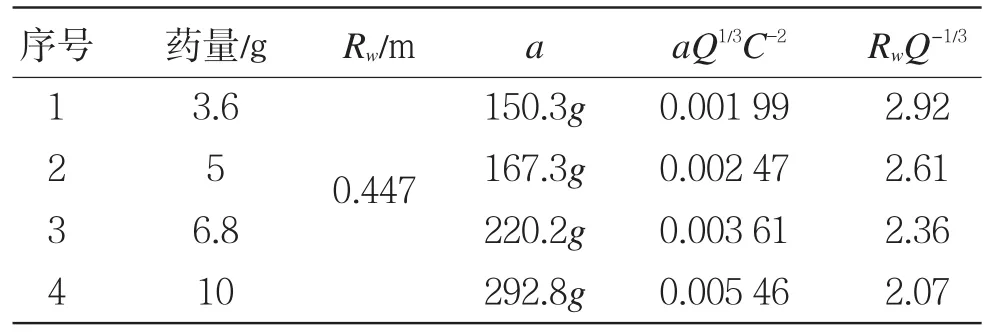
表3 测点C振动加速度实测数据Table3 Experimentaldataofmeasuring pointC

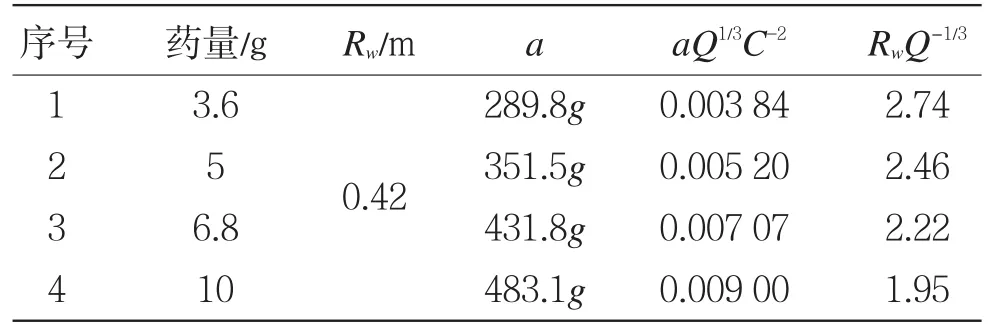
表4 测点D振动加速度实测数据Table4 Experimentaldataofmeasuring pointD

从图4可知，装药量的增加与振动主频没有明显的依赖关系，并且结构不同部位所处的振动主频也不相同，这是由结构自身的力学特点决定的。由爆炸容器的特征方程可知，其固有频率是其质量与刚度的函数，某一部位或构件发生损坏都会造成其振动主频发生改变[6]。由于密闭结构上某一部位或构件损伤时质量一般不会减少，所以振动主频的变化主要由其局部刚度的损失引起，因此可以将此部位或构件完好时的振动主频作为判断其是否受损的依据。

由图4a可以看到，中环面的壳体振动主频集中在固有基频（理论值f=1 462Hz）附近，说明振动能量主要集中于此。因此，可以采用在局部加强的方法以改变固有频率来避免谐振，提高容器的安全性能。

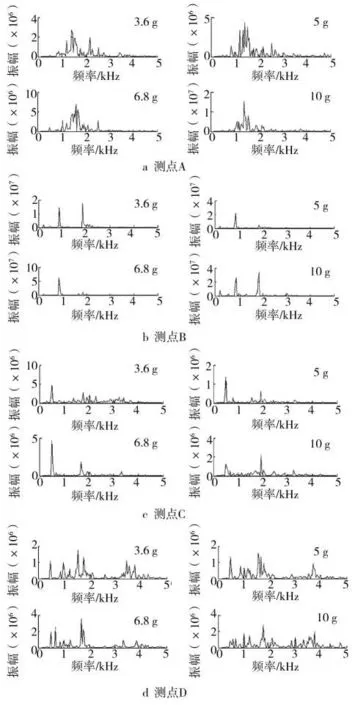
图4 振动加速度频谱Fig.4 The vibration acceleration frequency spectrum

由图4c，d可知，随着爆心距的增大，振动中出现了很多低频成分，而基频附近的频率逐渐减少，说明越靠近两端，具有较低频率的非轴对称弯曲振动越容易被激发。这主要是由于圆柱壳体并非完全对称造成的，如壳体上开的传感器孔、装药孔以及支座对壳体底部的支撑等；另外两端的边界效应逐渐增强也是原因之一。因此，可以通过减少壳体表面上的非对称结构，尽量将孔或盘类结构开设在中环面附近的方法来避免低频谐振。

对于容器封头处的振动频率，由图4b可知，其频率成分单一，主要由平板封头的固有频率决定，受圆柱壳体的固有频率影响不大。

2 基于SPSS的振动加速度经验公式

为了确定爆炸容器在承受内爆炸载荷时振动加速度峰值的位置，弄清在容器结构上的衰减规律，需要根据监测的试验数据回归出经验公式。从试验结果可以看出，振动加速度的大小不仅取决于爆炸当量，而且与爆心距密切相关。

对试验数据中的参量进行无量纲化，可以得到主要的无量纲参数有：比例加速度aQ1/3C-2和比例距离RwQ-1/3，它们存在如下关系式[7]：

式中：a为壳体结构冲击加速度；Q为装药量，kg；C为密闭容器中的声速，m/s；Rw为测点至爆心的距离，m；α，β为需要确定的参数。将式（1）两边取自然对数化简，可以得到线性回归模型：

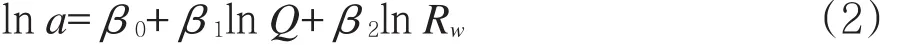
利用SPSS对其进行多元回归[8]，可以得到方程的所有系数，输出的结果及分析见表5。

表5中的确定系数R的值为0.979，符合因变量总变化中的97.9%，拟合效果较好。表6中非标准化的系数列中的回归系数就是预测的回归方程中的参数，代入式（2）就可以得到回归方程：

表5 回归模型汇总Table5 Theaggregation of regressionmodel

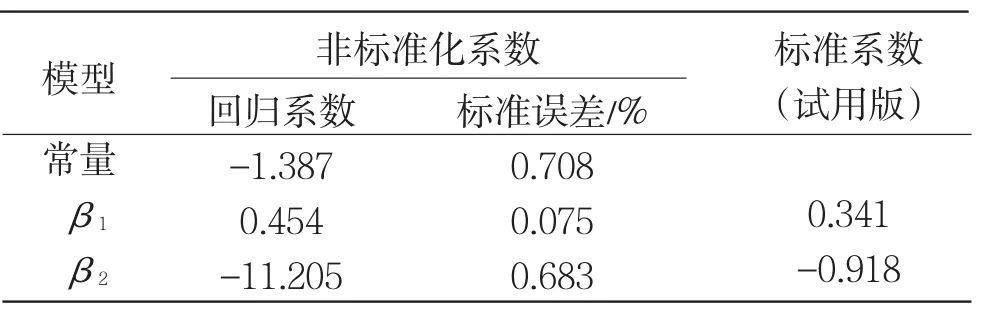
表6 回归模型的系数Table 6 The coefficientof regressionmodel

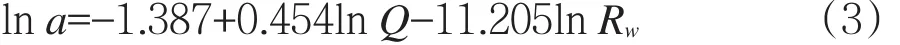
化简得经验公式：

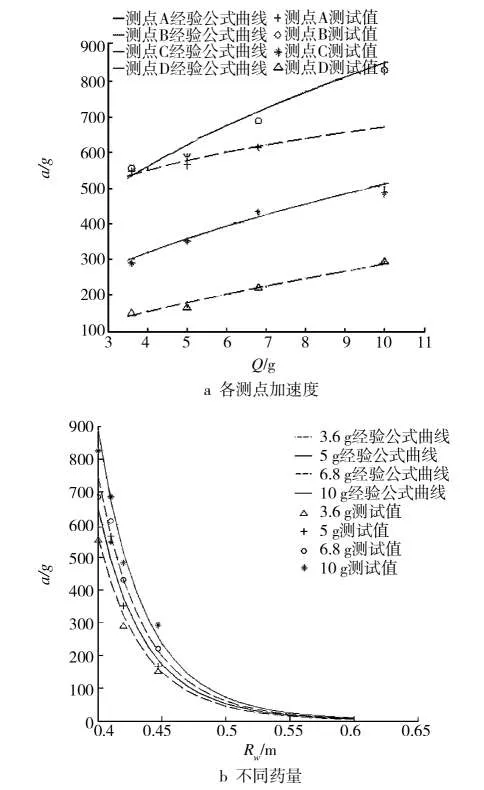
图5 拟合效果对比Fig.5 Comparison of fitted results

对于测点处加速度和药量以及与爆心距的关系，经验公式和试验值对比如图5所示。构件会呈现出不同的振动主频，且与载荷大小无关。因此，可以通过结构某一部位或构件完好时的振动主频作为判断其受损状况的标准，如某次测出的振动主频低于这个标准，即可判定此处可能发生损伤。同时，可以通过改变局部尺寸和减少非对称结构等方法防止和减少共振响应。

3）对于密闭结构上的振动参数，由试验数据回归分析得到的经验公式具有一定的工程应用价值，如已知起爆装药量，先由经验公式算出振动加速度，再由相似律推算出与爆炸容器结构相似的密闭结构的振动情况，加上安全系数，即可判断其结构是否受到破坏，检验安全设计是否合理；也可以根据爆炸容器正常工作的加速度耐振值，反算出最大起爆装药量，从而指导内爆炸试验。不过，该经验公式是由特定尺寸爆炸容器试验得出的，仅适用于与其结构相似的密闭结构加速度值计算，因而具有一定的局限性。