分数像素快速块匹配运动估计方法综述

陈志江，涂丹

（国防科技大学信息系统与管理学院系统工程系，湖南长沙410073）

运动估计（Motion Estimation，ME）是根据图像内容估计图像序列相对运动的方法，是计算机视觉领域的关键技术，由于其在压缩编码、视频稳像、目标跟踪、图像配准等方面有着重要应用，一直以来都是研究的热点，各种技术方案推陈出新、快速发展。一般说来，现有的运动估计方法可分为块匹配法、像素法、特征法和相位法等4类，其中块匹配方法由于简单高效，便于硬件实现，得到了推广使用，尤其在现在的视频压缩标准中有着非常重要的作用，被认为是最成功的运动估计方法。

块匹配运动估计是现有国际视频压缩标准中的核心技术，早期的标准如H.261中采用整像素运动估计（Integerpixel Motion Estimation，IME），后来的标准中则引入了分数像素运动估计（Fractional-pixel Motion Estimation，FME）来获得更高的压缩率与更好的图像重构质量[1]，如H.263、MPEG-1、MPEEG-2等标准中采用1/2像素精度的运动估计，H.264[2]中则引入了1/4和1/8像素精度的运动估计。

引入分数像素运动估计带来了压缩率与图像质量带来提升，但同时也带来了更大的计算量。文献[3]对H.264的计算复杂度进行了分析，得出其中IME与FME分别占总共编码过程计算量的52.034%和37.207%。混合编码结构中的运动估计总是分成两部分进行的，先进行整数像素运动估计，然后在整像素估计最优解的周围进行亚像素位置的搜索求解。随着整像素快速算法的提出与不断改进，已经能在仅检测5个搜索点的情况下找到最优解[4]。相比之下，分数像素的搜索求解计算量显得难以接受了，因此发展分数精度的快速运动估计算法，是有着迫切需求的，近些年来许多的学者都投身于其中的研究，取得了很多新的研究成果。

1 块匹配运动估计

1.1 块匹配运动估计基本原理

在自然视频中，由于场景的不变性与物体运动的连续性，视频图像内容在时间域上具有很强的相关性，通过运动估计得到这些相关性就能去除冗余数据达到压缩目的。现有视频压缩一般都是基于混合编码结构（Hybrid Coding Framework，HCF），其基本思想是将视频中的帧图像分成许多互不重叠的宏块（Macro Block，MB），并认为宏块内所有像素的运动偏移都相同，然后在参考帧中对每个宏块的特定搜索范围内根据一定的匹配准则找出与当前块最相似的匹配块，匹配块与当前块的相对位移即为运动矢量[5]。当前块与匹配块的差为残差数据，其值都较小，只对残差数据进行压缩，能够获得较大的压缩率。通过残差数据与运动向量，就可以完全恢复当前块。使用块匹配运动估计进行视频压缩的基本原理如图1所示。

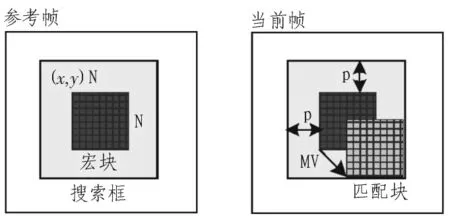
图1 视频压缩的基本原理Fig.1 Basic theory of video compression

实际中的运动是几乎不会以整像素为单位发生的，使用整像素为单位进行运动估计，必然造成残差数据过大，降低压缩性能，因此必须考虑精度更高的运动估计。文献[6]中对自然视频中的运动进行了统计，由于自然视频中的场景大都是静止的，所以超过90%的宏块整数像素运动估计和分数像素运动估计是一致的，但是仍然不能忽视分数像素的运动向量估计，即使是微小的分数像素精度错误偏移，都会带来比特率的明显增大。

1.2 分数像素插值算法

在自然视频图像中，图像的采样都是以整像素单位进行的，要进行分数像素精度的运动估计计算，则需要进行插值得到分数像素位置的值，一般使用的是双线性插值方法。但在实际的压缩编码中，分数像素位置常以1/2n为单位的，如在H.264中，运动估计需要达到1/4像素精度，其插值运算便分两步进行，先进行1/2像素的插值，再进行1/4像素的插值[7]。

如图2所示，1/2像素的位置可以分为与整像素相邻的和不相邻的两种，其像素值是通过在水平或垂直方向上使用6抽头FIR滤波器得到，滤波系数为（1，-5，20，20，-5，1）/32。其计算公式如式（1）所示：

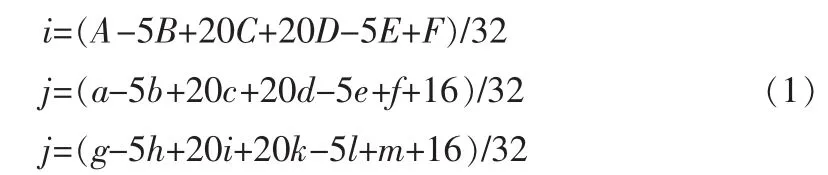
然后利用1/2像素位置和整像素位置值进行插值，便可以得到1/4像素位置的值。

图2 分数像素位置及其计算Fig.2 Calculation of fractional pixel in H.264

1.3 分数像素全搜索算法

整数像素的全搜索算法是逐个计算搜索框内每个点的费用函数值，最优值位置对应的向量即为运动向量。分数像素精度的全搜索算法，则是在整数最优解的附近搜索计算所有位置点的费用值从中选优的。由于分数像素精度是一个递进式的，有1/2像素精度、1/4像素精度、1/8像素精度等，这便形成了一个层次式的计算。以H.264中的1/4精度全搜索算法为例，其计算步骤如下：

步骤1全搜索求最优1/2像素点

如图3所示，其中的点O是整像素最优解，a-h标示的位置为1/2像素位置，则通过计算每一个位置的费用函数值，通过比较就能得出具有最优值的1/2像素位置。在H.264中使用拉格朗日函数作为费用函数，如公式（2）所示。其中m为运动向量；p为预测的运动向量；r为参考帧参数索引；λSAD为SAD失真准则的拉格朗日乘子；R为运动信息和所选则的参考图片r的码率。分数像素搜索时SAD是残差经过哈达码变换后的系数的绝对和。

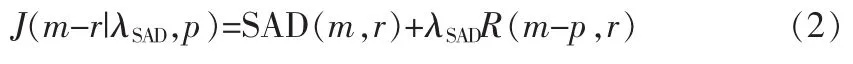
图3 分数像素搜索步骤Fig.3 Process of Fractional Full Search

步骤2求最优像1/4素点

得到最优1/2像素点后，以其为搜索中心，计算其周围的8个1/4像素点1-8的拉格朗日函数值，比较得出最优1/4像素位置。

从以上步骤可以看出，按相同的思路可以达到更高精度的搜索，但是若要达到1/2n精度的运动估计，则需要搜索计算8n个点的拉格朗日函数值，其中包含了计算量很大的插值运算，因此该算法的计算量是不可接受的，必须引入快速算法来解决分数像素运动估计问题。

2 分数像素运动估计快速算法

由于分数像素全搜索运动估计方法的计算量太大，成为压缩技术发展与应用的桎梏，近些年来许多学者致力于优化分数像素运动估计方法，提出了许多快速算法。现在发展的分数像素快速算法已经比较多了，但并没有一个很好的分类。通过对现有快速算法的分析发现，主要是从4个方面进行算法的优化：基于数学模型、基于向量预测、基于搜索优化、基于提前退出（Early Termination，ET）技术等。下面分别进行介绍。

2.1 基于数学模型

对于分数像素的运动估计，一个重要的前提假设就是在整数最优解的附近，误差曲面是一个单调凸函数，如图4所示。基于数学模型的方法，就是利用数学函数对误差曲面进行拟合，然后通过整数最优解位置及周围8个点的误差费用值求解未知参数，再利用求解出的参数估计分数像素位置的SAD值，从而达到分数像素的运动估计精度。主要有二次曲面模型、二次曲线模型和线性模型等。

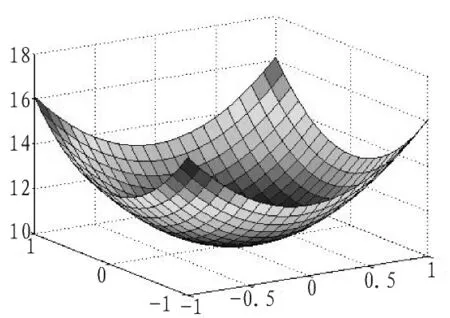
图4 典型的SAD误差曲面Fig.4 Typical SAD distortion surface

2.1.1 二次曲面模型

文献[8]提出了3种参数个数不同的二次曲面模型，分别有9个、6个、5个参数，并且在6参数和5参数模型的基础上提出了加权的改进模型。其中9参数模型是用任意的平滑曲面来对误差曲面进行拟合，公式如（3）所示，其自由度最大，精度也较高，但参数较多也带了计算复杂度大的问题。6参数模型将9参数模型中的高次项忽略，用投影为椭圆的曲面来进行拟合，公式如（4）所示。5参数模型进一步对高次项进行了忽略与简化，公式如（5）所示。这3种模型如图5所示，从左到右依次为9参数模型曲面，6参数模型曲面投影，5参数模型曲面投影。文献还对6参数模型和5参数模型进行了改进，给整像素点赋予不同的权重，提出了加权二次曲面模型，具有更大的灵活性与准确度。

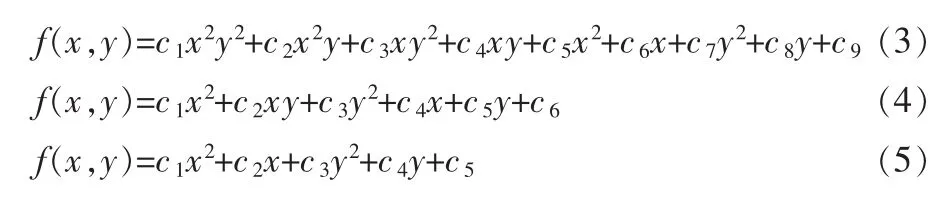
2.1.2 二次曲线模型

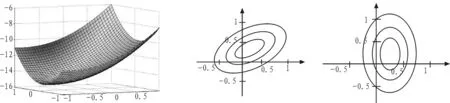
图5 3种二次曲面模型图示Fig.5 Three kind of conicoid model

对于曲面模型，当令x或y为定值时，可得到曲面与该切面的相交线，即为二次曲线。对误差曲面建立9参数模型：

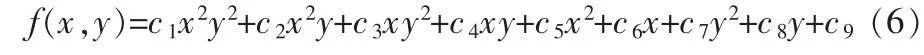
当令x=k时有：

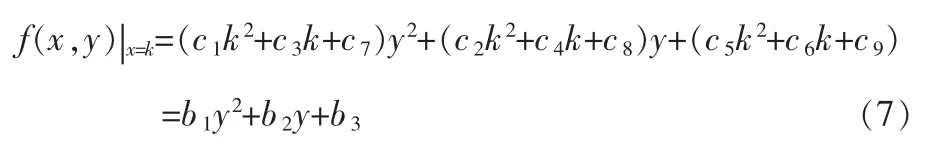
同理，当y=g时有：

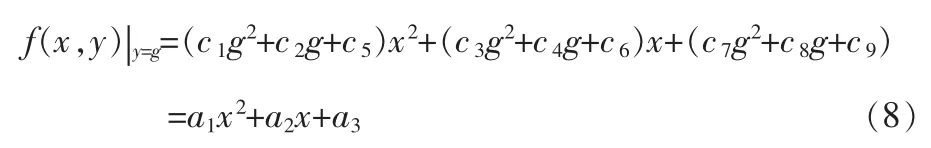
因此在水平和竖直方向上能得到2个一元二次曲线函数，如图6所示。

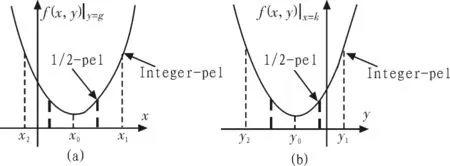
图6 二次曲线模型Fig.6 Conic model

文献[9]利用二次曲线进行建模，通过整像素函数求解参数然后计算分数像素位置的值。该方法计算1/2精度时需要引入4个扩展位置的计算，总共计算12个点的值，由于使用二次曲线模型，计算量相比曲面模型大大减少。文献[10]基于二次曲线模型提出一种HADP模型，将五参数的二维曲面函数分解为x，y两维上的三参数抛物线模型，然后直接估计最优解的位置，在位置附近搜索2～3点，以增加算法的鲁棒性。该方法可在不同的分辨率精度上使用不同的值来估计参数，从而更加精确。实验表明，该方法节省了大量的计算量，对PSNR的影响较小。

2.1.3 线性模型

文献[11]对误差曲面建模进行了进一步的简化，使用线性函数来估计SAD曲面模型（如图7所示）。对于已知的3个整数点的值，文献中提出使用两条具有相同斜率值的对称直线来进行建模，这种建模方法十分简单，大大减少了运算量。

总的说来，使用数学模型的好处是可以直接计算出亚像素位置的SAD值，避免了进行分数像素值运算和之后的二次搜索，从而大大减少了计算量。但是数学模型计算出来的SAD值与实际的值是存在误差的，算法准确度不是很高，因此在很多文献中数学模型方法只是用来提供预测信息来进行搜索优化，如文献[12]提出一种基于退化的二次函数的预测方法，先通过二次曲面模型直接求解极值点，将解量化至1/4像素精度位置，然后使用CBFPS[13]算法精细求解。

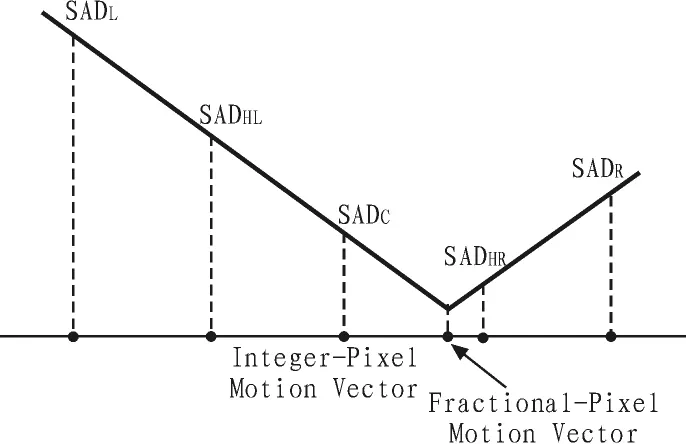
图7 线性模型Fig.7 Linear model

2.2 基于向量预测

向量观测技术最早被提出用来查找整数运动估计中的全局最优解的点，这种方法在分数像素运动估计中也被广泛使用。文献[14]中提出了4种预测向量，空间域上两种，时间域上两种。运动估计中的预测向量大都是这4种思路，下面分别进行介绍。

1）中值预测（Median Prediction，MP）

由前面的介绍可知，视频压缩中是将图像划分为互不重叠的宏块来进行运动估计的，在进行当前块运动估计时，左、上、左上和右上的邻块的运动向量已经在前面的计算中得出，图像内容在很多时候是具有整体性的，因此认为当前块与邻块的运动向量具有很强相关性。这里使用邻块运动向量的中值来进行预测，称之为中值预测。如图8所示，A、B、C、D分别为当前块的邻块，对应的向量为则中值的计算公式为：

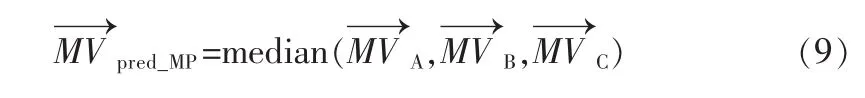
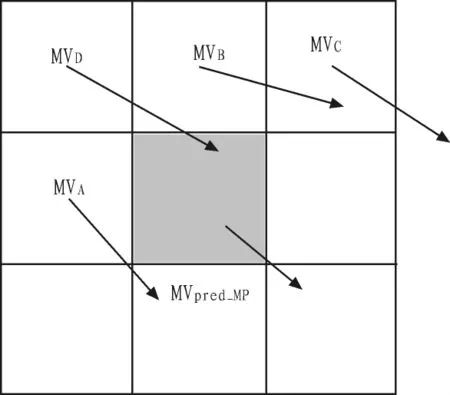
图8 中值预测Fig.8 Median prediction

2）上层预测（Up-layer Prediction，UP）

在H.264的标准中，宏块的尺寸大小有7种，如图9所示。在早期的JM参考软件中，先进行8×8的模式搜索，再进行16×16的；后来的版本中改成了先16×16后8×8了，依照的顺序是1到7的层次结构顺序。由于使用层次结构，可以使用大尺寸的搜索模式来预测小尺寸搜索模式的向量，称之为上层预测。如5和6是7的上层，1是2和3的上层。具体的预测公式如下所示：

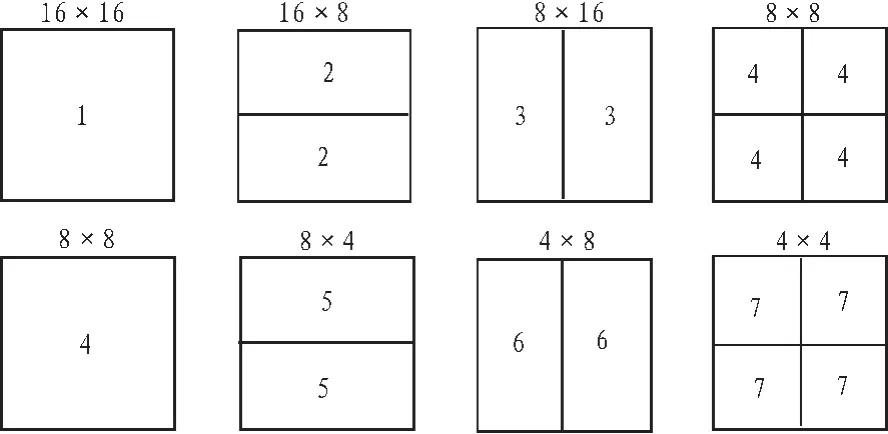
图9 宏块尺寸Fig.9 Size of macro-block

3）对应块预测（Corresponding-block Prediction，CP）

对于自然视频的图像序列，若没有发生场景的改变，帧图像之间的内容的相关性是非常大的。基于这种时间域上的相关性，可以用前一帧相对应位置的块的运动向量来预测当前块的向量，计算公式如下：

4）加速时间预测（Neighboring Reference-picture Prediction，NRP）

在H.264标准中使用了多参考帧运动补偿技术来增强预测的精度与编码的效率。对于同一宏块位置，在不同的参考帧中也是有着很强的相关性的。如图10所示，假设宏块的运动是匀速的，那么可以通过参考帧之间的时间差与宏块运动向量的比例关系来进行预测。其计算公式如下：

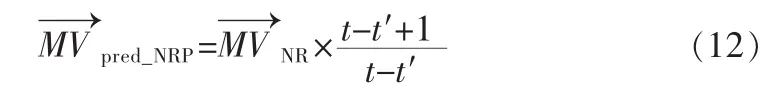
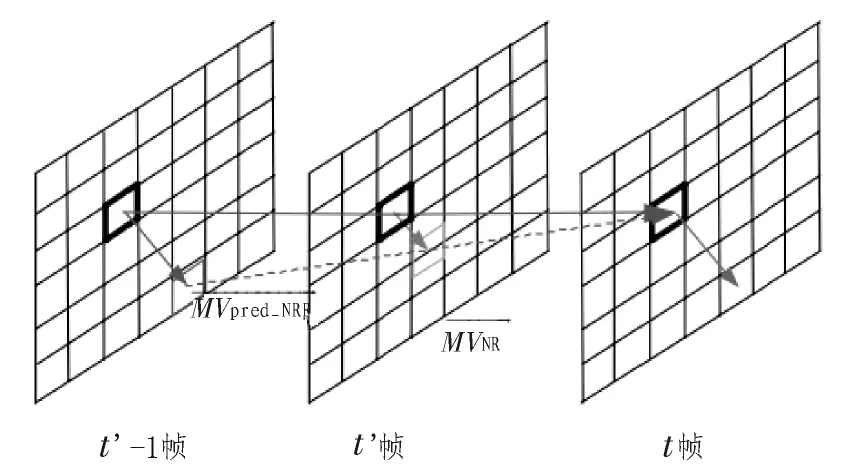
图10 加速时间预测Fig.10 Neighboring reference-picture prediction

前面所介绍的4种预测向量，MP与UP是从空间域上出发考虑的，CP和NRP是从时间域上出发考虑的。文献[14]对这4种预测向量进行了比较分析，发现空间域上的向量预测准确性要更大，UP的准确度最高，而MP随着宏块尺寸的越小准确度越高，因为宏块划分越小它们之间的运动相关性越大。文中给出的建议是先考虑MP再考虑UP来预测搜索的起始点。

前面关于预测向量的分析与介绍是基于整像素运动估计的，但很显然，当引入分数像素运动估计时，这4种预测仍然成立。以中值预测为例，定义M—→Vpred_MP为包含分数部分的预测向量（邻块A、B、C、D的分数像素精度已知，可通过前面的公式进行计算），在进行分数像素精度搜索时当前块的整像素运动向量是已经求解出来的，则可通过公式（13）预测分数像素向量的值。在1/4精度时式中β=4，1/8精度时β=8。

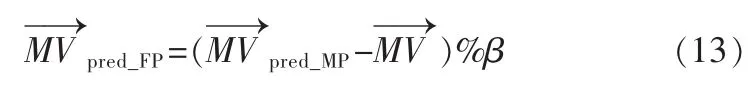
CBFPS是典型的基于预测向量的分数像素搜索算法，已经被H.264标准采用。该算法使用前面提到的中值预测估计出一个预测位置，计算出当前中心位置与预测位置的拉格朗日费用函数值，选择费用较小的位置进行小菱形模板迭代搜索，直到最优解在小菱形模板的中心。文献[15]在CBFPS的基础上进行了改进，提出一种仅需六个搜索点的单迭代算法（SIFME）。SIFME方法根据最优分数像素位置在预测位置周围的概率更大这一假设，直接搜索中心点，预测点及预测点对应的4个菱形位置点，直接从中挑选最优的解，而不再进行迭代搜索。实验表明，与全搜索相比，该方法虽然忽略了几乎88%的搜索点，但仍有60%～90%的正确率，而且该方法十分简单，易于使用硬件实现。

通过预测向量能够大大减少搜索量，因此在这基础上发展了很多方法，如同时考虑中值预测与上层预测的PDFPS算法[16]，基于候选预测集（Candidate Predictors Set）的HAPBPFPS算法[17]等，这里不再进行一一介绍。

2.3 基于搜索优化

基于搜索优化的方法，其出发点与整像素快速运动估计方法相似，主要是从搜索步骤、模式或中间搜索结果的关系来进行优化，减少对不必要点的搜索。

文献[18]充分利用分数像素位置间费用值的高度相关性，将搜索点减少到8-9个，该方法较为简单，便于硬件实现，文献中还给出了其VLSI结构，比文献[19]中的方法节省了约40%的硬件空间。如图11所示，算法的具体步骤如下：

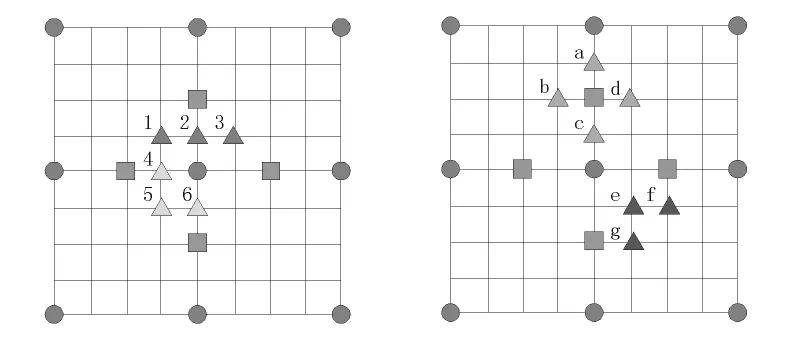
图11 算法过程Fig.11 Process of the algorithm

1）计算整数最优解位置和周围4个小菱形位置点的费用值。

2）根据计算结果的4种情况分别进行处理：

①当最优解在中心，次优解与第3优解不相邻时，搜索图中的1、2、3所示的位置。

②当最优解在中心，次优解与第3优解相邻时，搜索图中的4、5、6所示的位置。

③当最优解与次优解都不在中心并且相邻时，搜索如图中的e、f、g所示的位置。

文献[20-21]利用前面提到的5参数模型对误差曲面进行拟合求解得出预测最优解的位置，在附近进行优化搜索得到最终解，该方法在1/2精度时只需搜索3个点，1/4精度时只需搜索6个点。文献[22]提出了一种1/2像素精度的两步估计算法，该算法基于误差曲面单调性假设，先后分别在水平和竖直方向上进行计算搜索，比较得出最优值。与全搜索算法相比，该算法保持着几乎同样的图像质量与比特率，但计算量减少了一半。文献[23]提出了一种基于纹理方向分析的快速亚像素运动估计算法。该算法基于的基本思想是，在有纹理的图像中，垂直纹理方向进行亚像素的运动偏移更能够减小运动估计时的误差。通过最优解与次优解的位置关系，将1/4像素精度的搜索位置减少至4～5个点。陆寄远[24]等人利用分数点残差曲面的单峰特性和整分数运动向量的相关性，通过优化搜索模板和搜索的起始位置，在菱形模板的基础上提出动态剪裁策略，有效加快了搜索的速度。

基于搜索优化的算法的最大特点就是比较便于硬件的实现，而这一点也是近年来分数像素快速块匹配方法的发展趋势。

2.4 基于提前终止

所谓提前终止技术（Early Termination，ET），就是通过设置各种阈值来减少不必要的搜索，当某一条件达到阈值门限时就及时退出搜索过程。使用提前终止技术要达到两个目的，一是越早退出越好，这样能减少更多的搜索量；二是要使得退出前得到的运动向量越接近最优向量越好（这里指的最优向量是以全搜索得到的结果为参考的）。当然，很多时候这两个目的是有所冲突的，这使得提前终技术中的阈值设置很有难度。

提前终止技术对算法本身没有具体的要求，能够与许多算法进行配合来优化加速。文献[18]中使用自适应线性预测阈值来进行提前终止，能够提高8.5%～14%的速度。文献[24]主要对整像素的快速算法ARPS-3提出了两点改进，一是通过设置自适应搜索阈值T来进行提前终止，二是通过设置队列标记已搜索的点避免重复搜索。文章也将提前终止技术的扩展到分数像素精度，在1/2精度时使用0.95T作为阈值，在1/4精度时使用0.9T作为阈值。

提前终止技术不仅仅只是从像素点位置的SAD值上进行考虑的，如文献[25]提出的一种SQIA方法，该方法从视频帧、搜索块的两个层次进行阈值设置，当达到阈值时便跳过当前帧或当前块的1/4搜索，同时还对搜索点进行了优化处理，获得了很好的加速效果。

3 结束语

本文对分数像素块匹配运动估计方法的基本原理进行了介绍，对于现有的快速分数像素运动估计算法，主要是运用数学模型、向量预测、搜索优化、提前终止这4种技术来进行加速的，本文对这4种技术的基本原理和代表算法进行了介绍。值得注意的是，本文介绍的4种技术是能够较好的相融与组合，使其发挥更好的加速效果的。

分数像素的运动估计是H.264标准中的重要部分，带来了视频质量与压缩率的提升，但同时也带来了更多的计算量。最新视频压缩标准中，将分数像素的运动估计精度扩展到1/8像素。现有许多快速算法能够较大减少计算的复杂度，但是各有优缺点，或算法较为复杂不便于硬件实现，或参数选择较为困难等。分数像素运动估计的精度不是无限提高的，从近年发表的论文来看，该领域的研究重心慢慢转向于发展快速简单的算法，以便于从硬件角度实现实时编码。此外，分数像素运动估计在其他领域的相关应用也是值得思考的问题。

[1] FURSHT B，JOSHUA G，RAYMOND W，Motion estimatio algorithm for video compression[M].London（UK）:Kiuwer Academic Publishers，1998.

[2] ITU-T Rec.H.264/ISO/IEC 14496-10 AVC.Draft ITU-T Recommendation and Final Draft International Standard of Joint Video Specification[S].Mar，2003.

[3] HUANG Y W，HSISH B Y，CHIEN S Y，el al.Analysis and complexity reduction of multiple reference frames motion estimation in H.264/AVC[J].IEEE Transactions on Circuits And Systems for Viedo Technology，2006，16（4）:507-522.

[4] BANH X Q，TAN Y P.Adaptive Dual-Cross search algorithm for block-matching motion estimation[J].IEEE Trans.Consumer Electron，2004，50（2）:766-775.

[5] MULLA MI，CANAKRAJA.C N.Video coding for mobile communication:Efficiency，complexity&resilience[M].Boston:Academic Press，2002.

[6] WANG Y J，CHENG C C，CHANG TS，A fast algorithm and its VLSI architecture for fractional motion estimation for H.264/MPEG-4 AVC video coding[J].IEEE Transactions on Circuits And Systems for Viedo Technology，2007，17（5）:578-583.

[7] Jain D S，Nal D S L，A fast fractional pel motion estimation algorithm[J].International Journal of Advanced Engineering&Applications，2010，I&II:118-124.

[8] SUH J W，JEONG J.Fast sub-pixel motion estimation techniques having lower computational complexity[J].IEEE Transactions on Consumer Electronics，2004（50）:968-973.

[9] Mohammed Sayed，Wael MB，Graham J.Low-complexity algorithm for fractional-pixel motion estimation[C]//International Conference on Image Processing（ICIP）.DOI:10.1109/ICIP.2009.5414600.2009:1565-1568.

[10] Yi-long LIU，Soontorn O.Fractional-pel motion refinement based on hierarchical adjustable dual-parabola model[C]//Communications and Information Technology，2004.ISCIT 2004.IEEE International Symposium on，2004:752-755.

[11] Yun-gu Lee，Jae Hun Lee，Jong Beom Ra.Fast half-pixel motion estimation based on directional search and a linear model[C]//Taiwan:Visual Communications and Image Processing（VCIP），2003:1513-1520.

[12] CHANG Jing-fu，LEOU Jin-jang.A quadratic prediction based fractional-pixel motion estimation algorithm for H.264[C]//in Proc.Seventh IEEE International Symposium on Multimedia（ISM'05），2005:491-498.

[13] CHEN Z B，ZHOU P，HE Y.Fast integer pel and fractional pel motion estimation for JVT[C]//Awaji，Japan:JVT-F017，6th metting，2002:5-13.

[14] Zhi-bo CHEN，Jian-feng XU，Yun HE，et al.Fast integerpel and fractional-pel motion estimation for H.264/AVC[J].Journal of Visual Communication and Image Representation（JVCIR），2006，17（2）:264-290.

[15] Tzu-Yun Kuo，Yu-Kun Lin，Tian-Sheuan Chang.SIFME:A single iteration fractional-pel motion estimation algorithm and architecture for HDTV sized H.264 video coding[C]//International Conference on Acoustics，Speech，and Signal Processing（ICASSP），2007:I-1185-I-1188.

[16] YANG Li-bo，YU Ke-man，LI Jiang，et al.Predictionbased directional fractional pixel motion estimation for H.264 video coding[C]//in Proc.IEEE International Conference on Acoustics，Speech，and Signal Processing（ICASSP2005），2005（2）:901-904.

[17] Hong-yang CHAO，Ji-yuan LU.A high accurate predictor based fractional pixel search for H.264[C]//International Conference on Image Processing（ICIP）2006:2365-2368.

[18] Tung-Chien CHEN，Yu-Wen HUANG，Liang-Gee CHEN.Fully utilized and reusable architecture for fractional motion estimation of H.264/AVC[C]//International Conference on Acoustics，Speech，and Signal Processing（ICASSP）.2004（4）:9-12.

[19] Chen T C，Huang Y W，Chen L G.Fully utilized and reusable architecture for fractional motion estimation of H.264/AVC[C]//in Proc.ICASSP，2004（4）:9-12.

[20] DU C，HE Y，ZHENG J.PPHPS:A parabolic predictionbased，fast half-pixel search algorithm for very low bit-rate moving-picture coding[J].IEEE Transactions on Circuits And Systems for Video Technology，2003，13（6）:514-518.

[21] Zhi-bo CHEN,Cheng DU,Jing-hua WANG,et al.PPFPSA paraboloid prediction based fractional pixel search strategy for H.26L[C]//IEEE International Symposium on Circuits and Systems（ISCAS）.DOI:10.1109/ISCAS.2022.1010147，2002:9-12.

[22]ZHOU Bo，CHEN Jian.A fast two-step search algorithm for half-pixel motion estimation[C]//10th IEEE International Conference on Electronics,Circuits and Systems，2003:611-614.

[23] Hoi-ming Wong,Oscar C Au,Andy Chang.Fast sub-pixel inter-prediction-based on texture direction analysis[C]//IEEE International Symposium on Circuits and Systems（ISCAS）.DOI:10.1109/ISCAS.2005.1465876，2005:5477-5480.

[24] WEI Z,JIANG B,ZHANG X,et al.A new full-pixel and sub-pixel motion vector search algorithm for fast blockmatching motion estimation in H.264[J].in Proc.Int.Conf.Image Graph.，2004：345-348.

[25] Hoi-Ming Wong,Oscar C Au,Jin-xin Huang,et al.Suboptimal quarter-pixel inter-prediction algorithm（SQIA）[C]//International Conference on Acoustics,Speech,and Signal Processing（ICASSP）.2005:II-921-II-924.