有理四次样条曲线的点控制

唐 烁， 徐 刚

（合肥工业大学数学学院，安徽合肥 230009）

样条插值是计算机辅助几何设计中的强有力工具，研究人员已经研究了不少类型的样条插值用于几何造型的控制设计［1－3］。然而，由于在给定的插值点处插值曲线的唯一性，仅有一些方法被用来作形状控制［4－7］。为了满足日益复杂的设计要求，曲线曲面设计中的形状控制变得越来越重要。近些年来，有理样条，特别是有理三次样条的研究在理论上已取得许多成果，它们在形状控制方面的应用已引起了广泛的兴趣。由于有理插值函数表达式中带有参数，因而可以在插值条件不变的情况下通过对参数的选择进行曲线的局部修改，给控制插值曲线的形状带来方便。

有理四次插值曲线由于其构造所花费的计算量太大以及在使用上的不方便而让人们忽略了其重要的应用价值，因而以前很少有人研究。但近年来，有理四次插值样条是比较热门的研究课题［8－11］。实际上，在某些情况下，有理四次插值样条有其独特的应用效果，比如文献［8］建立的一种具有局部插值性质的分母为二次的有理四次样条，即一个剖分子区间上的有理插值式只与邻近区间上的插值点有关，一个插值节点上的数值变动只影响其邻近的局部范围；文献［9］构造了一种分母为线性的有理四次插值样条，研究得到了该种有理四次插值样条不但具有三次多项式的插值精度，而且具有独特的逼近性质；文献［10－11］先构造了有理四次插值样条，讨论了插值样条的保单调性、C2连续性以及逼近性质，然后将其推广到有理双四次插值曲面。这些插值函数一般都用到被插函数的函数值和导数值，然而，在实际应用中，有时导数值是很难得到的，因此，研究仅基于函数值的有理样条插值的性质和应用效果是非常有意义的。文献［12］讨论了将仅基于函数值的分母为线性的有理三次插值样条曲线约束于给定区域的充要条件；文献［13－14］讨论了仅基于函数值的分母为二次的有理三次插值样条曲线的点控制问题，给出了函数值控制、导数值控制和拐点控制的情况。本文主要研究了仅基于函数值的分母为线性的有理四次插值样条曲线的点控制问题。

1 基于函数值的有理四次插值样条

给定点集｛（ti，fi），i＝0，1，…，n＋1｝，其中a＝t0＜t1＜…＜tn＋1＝b是插值节点，fi是被插函数f（t）在节点ti的函数值。记hi＝ti＋1－ti，θ＝（t－ti）／hi，Δi＝（fi＋1－fi）／hi，并且令参数δi＞0，则建立的保证C1连续的插值函数如下：

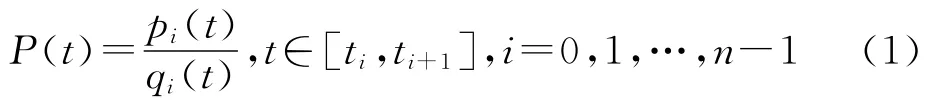
其中

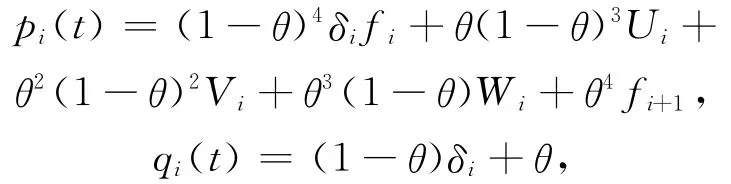
显然插值函数P（t）满足：

很容易证明对于给定的插值节点（ti，fi）和参数δi，插值函数存在且唯一。对于上面建立的有理四次插值样条，Ui、Wi的取值可以保证函数的C1连续性。

考虑等距节点的情况，即hi＝hj，i，j∈｛1，2，…，n｝，此时（1）式可以改写为：

其中

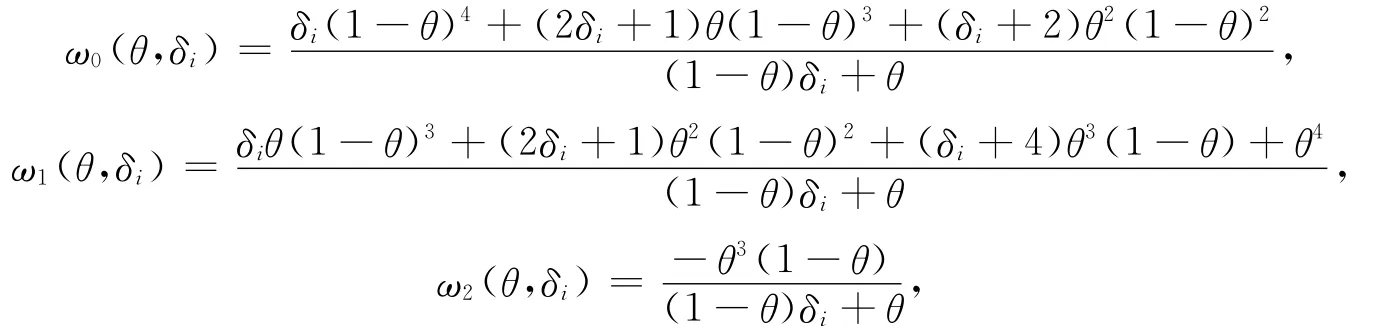
称ωr（θ，δi），r＝0，1，2为插值基函数，容易证明ωr（θ，δi）满足

2 插值函数的有界性

考虑插值函数的有界性，对于给定的等距插值节点，插值函数在插值区间内具有和参数δi无关的有界性，如定理1所述。

定理1 假设f（t）∈C2［a，b］，等距划分Δ：a＝t0＜t1＜…＜tn＜tn＋1＝b，对于给定的参数δi，P（t）是（2）式定义在区间t∈［ti，ti＋1］上的有理四次插值样条。令则对于任意δi＞0，P（t）在

证明 显然ω0（θ，δi）＞0，ω1（θ，δi）＞0，ω2（θ，δi）＜0，很容易得出：

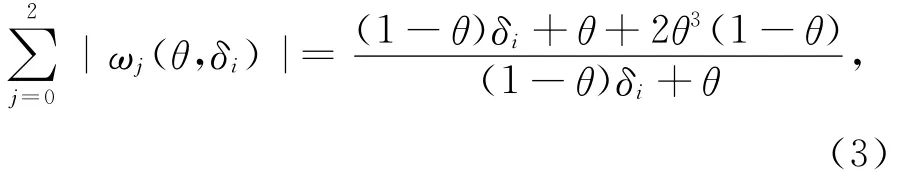
利用导数很容易算出当θ＝2／3时g（θ）取得最大值，所以有g（θ）≤35／27，定理1证明完毕。

3 插值曲线的局部点控制

插值区间上插值曲线的形状依赖于插值点，一般来说，当插值点给定之后，由于插值函数的唯一性，插值曲线的形状是固定的。但是在（2）式中存在一个独立的参数δi，尽管插值条件不变，通过选择合适的参数可以对曲线的形状进行修改。

假设要求插值曲线在t＊∈［ti，ti＋1］处的值P（t＊）＝M，显然M必须满足定理1，令θ＊＝（t＊－ti）／hi，则有：

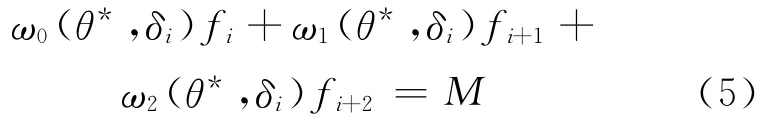
文献［11］称（5）式为控制方程，这种控制方法称为函数值控制。显然（5）式等价于：

其中

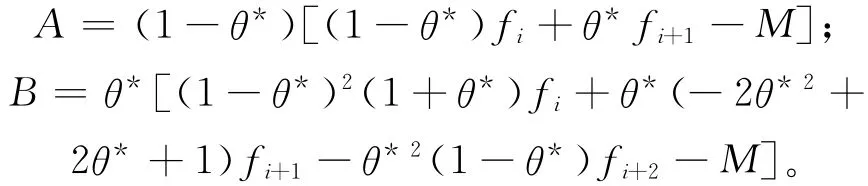
称（6）式为条件方程，显然如果存在δi＞0满足（6）式，那么（5）式也成立，从而有下面的定理2。

定理2 假设P（t）是通过（2）式定义在区间上的插值函数，t＊则存在δi＞0，使得（6）式成立的充分条件是AB＜0。

假如实际设计要求：

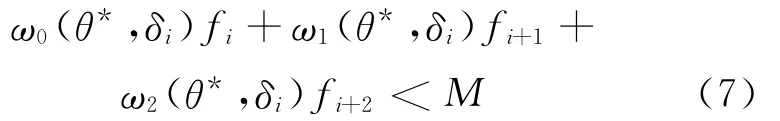
那么（7）式等价于：

其中，A、B为（6）式中所定义。相似地，如果存在δi满足（8）式，那么δi也满足（7）式。如果A、B之中存在一个负数，那么一定存在δi＞0满足（8）式，从而有下面的定理3。

定理3 对于上面定义的不等式（8）式一定有解δi＞0的充要条件是A≥0，B≥0不能同时成立。

假设实际设计要求控制插值函数在一点处的斜率，令t∈［ti，ti＋1］，θ＝（t－ti）／hi，N∈R，如果要求P′（t）＝N，从而

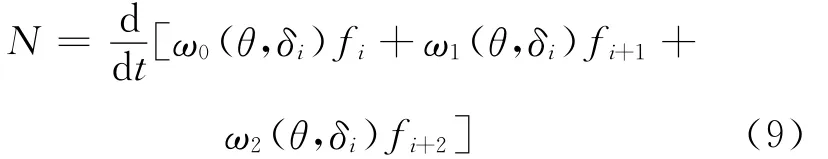
方程（9）式整理成：

其中

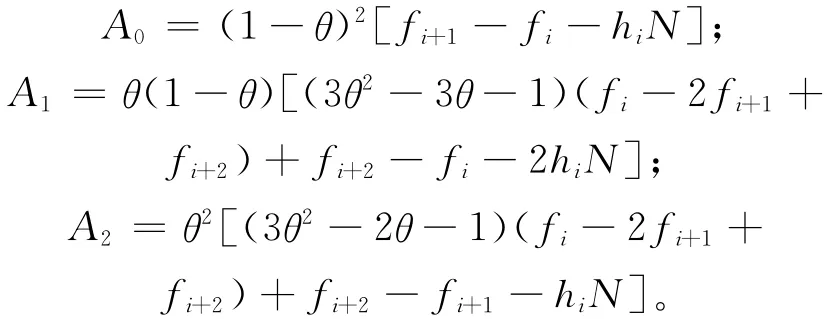
（10）式是关于δi的二次方程，如果（10）式存在正根，那么（9）式成立。这种方法称为导数值控制。

定理4 假设P（t）是通过（2）式定义在区间［ti，ti＋1］上的插值函数，t∈［ti，ti＋1］，N∈R，那么∃δi＞0满足P′（t）＝N的充要条件是方程（10）式有正根。

如果设计要求：

控制不等式（11）式等价于：

其中，A0、A1、A2为（10）式所定义，从而有下面的定理5。

定理5 对于给定的插值条件，控制不等式（11）式成立的充要条件是∃δi＞0满足（12）式。

例1 给定插值节点f（0）＝1，f（1）＝3，f（3）＝2，假如P（t）是通过（2）式定义在区间［0，1］插值样条函数，显然θ＝t，下面给出函数值控制的例子。

令δi＝2，则P1（t）＝（－3t4＋3t3－2t2＋3t＋2）／（－t＋2），t∈［0，1］，计算得出P1（0.4）＝1.872 0。

对于给定的插值点，如果设计要求P（0.4）＝2.0，控制方程（5）式为：0.12δi－0.035 2＝0，计算可得δi＝22／75，从而插值函数为P2（t）＝（－225t4＋225t3＋106t2＋97t＋22）／53t＋22，t∈［0，1］。

如果设计要求P（0.4）＝1.85，控制方程（5）为：0.03δi－0.095 2＝0，计算可得δi＝238／75，从而插值函数为：P3（t）＝（－225t4＋225t3－326t2＋313t＋238）／（－163t＋238），t∈［0，1］。图1所示为P1（t）、P2（t）、P3（t）的图形。

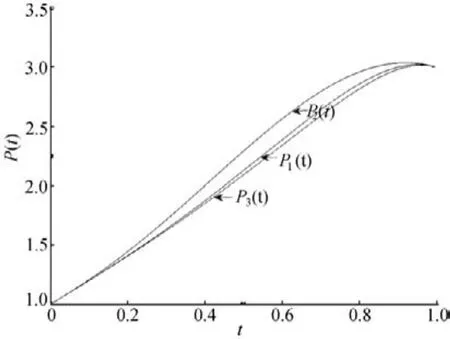
图1 P1（t）、P2（t）、P3（t）曲线

例2 给定插值节点f（0）＝2，f（1）＝4，f（2）＝－1，假如P（t）是通过（2）式定义在区间［0，1］插值样条函数，显然θ＝t，下面给出导数值控制的例子。

令δi＝2，则P4（t）＝（－7t4＋7t3－2t2＋2t＋4）／（－t＋2），t∈［0，1］，计算得出3.361 1；对于给定的插值条件，如果设计要求此时方程（10）式为0，计算得出根小于0），从而如果设计要求3.75，此时（10）式为计算得出δi＝1（另一根为0），从而t∈［0，1］。显然此时P6（t）退化为多项式插值。

图2 P4（t）、P5（t）、P6（t）曲线

4 插值曲线的拐点控制

函数的拐点依赖于函数的二阶导数，在给定等距节点的条件下，P（t）的二阶导数如下：

其中，B0（θ）＝3（1－θ）3；B1（θ）＝θ（6θ2－10θ＋3）；B2（θ）＝θ2（1－3θ）。

定理6 假设P（t）是通过（2）式定义在区间［ti，ti＋1］上的插值函数，t＊∈（ti，ti＋1），则∃δi＞0使得P”（t＊）＝0的充要条件为2ti／3＋ti＋1／3＜t＊＜ti＋1。

定理6说明了P（t）的拐点θ＊必在内，而且从证明的过程中可以看出，当给定插值节点后，P（t）拐点的位置只与参数δi有关，与插值节点处的函数值是无关的。另外，由于函数的凹凸性也与二阶导数有关，因此有下面的定理7。

定理7 假设P（t）是通过（2）式定义在区间［ti，ti＋1］上的插值函数，t＊∈（ti，ti＋1），P（t）在点（t＊，P（t＊））处是凸的充分条件是∃δi＞0，使得

由定理5的证明可以看出，当t＊∈（ti，2ti／3＋ti＋1／3），M（θ＊，δi）＞0，因此插值曲线在区间（ti，2ti／3＋ti＋1／3）的凸凹性完全由fi－2fi＋1＋fi＋2的符号决定。

例3 利用例1中的插值节点，给出拐点控制的例子。

令M（θ，δi）＝0，设θ＊＝0.4，则方程2δi－4＝0的根为（另一根小于0），其中，假设θ＊＝0.6处函数是凸的，那么由不等式－21δi－12＞0，取δi＝4，此时插值函数为：P8（t）＝（－3t4＋3t3－6t2＋5t＋4）／（－3t＋4），t∈［0，1］。图3所示为P7（t）、P8（t）的曲线图。

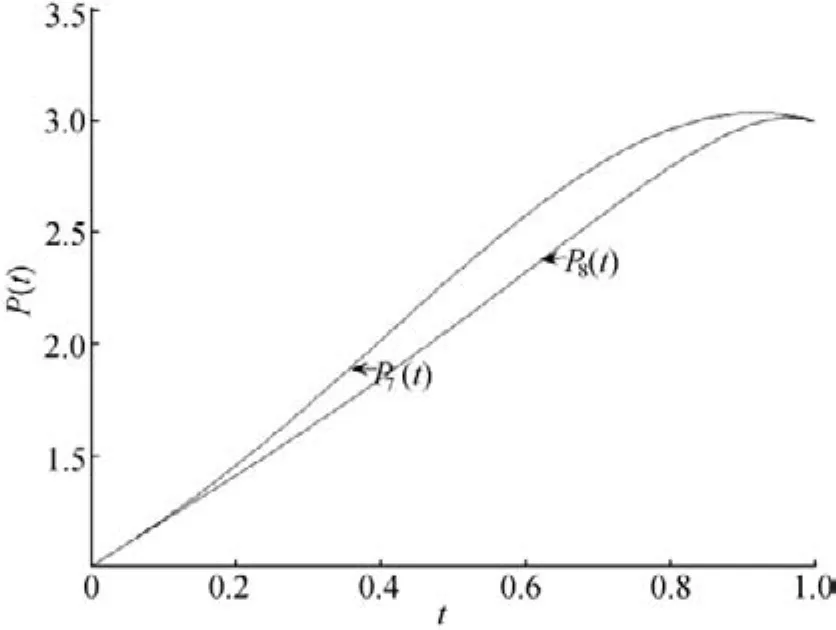
图3 P7（t）、P8（t）曲线

5 结束语

本文建立了一种仅基于函数值的分母为线性的有理四次插值样条，并分析了其性质，给出了在等距节点情况下的点控制方法，包括函数值控制、导数值控制和拐点控制。这些控制方法能够在插值条件不变的情况下，通过选取合适的参数来修改曲线的形状，从而满足实际设计的要求。相似地，在非等距情况下的插值函数P（t）为：

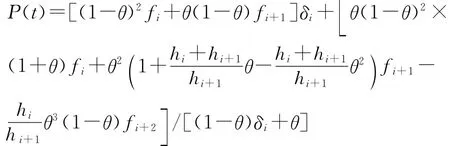
同样可以得到在非等距情况下的函数值控制、导数值控制和拐点控制方法。

［1］ Barsky B A.Theβ－spline：a local representation based on shape parameters and fundamental geometric measure［D］.Salt Lake City：University of Utah，1981.

［2］ Dierck P，Tytgat B.Generating the Bézier point ofβ－spline curve［J］.Computer Aided Geometric Design，1989，6（2）：279－291.

［3］ Foley T A.Local control of interval tension using weighted splines［J］.Computer Aided Geometric Design，1986，3（2）：281－294.

［4］ Duan Q，Wang L，Twizell E H.A newC2rational interpolation based on function values and constrained control of the interpolant curves［J］.Appl Math Comput，2005，161：311－322.

［5］ Duan Q，Wang L，Twizell E H.A new approach to the convexity control of interpolant curves［J］.Commun Numer Methods Eng，2003，19：833－845.

［6］ Duan Q，Djidjeli K，Price W G，et al.The approximation properties of some rational cubic splines［J］.Int J Comput Math，1999，72：155－166.

［7］ Duan Q，Djidjeli K，Price W G，et al.Weighted rational cubic spline interpolation and its application［J］.J Comput Appl Math，2000，117：121－135.

［8］ 叶懋冬.关于具局部插值性质的样条［J］.计算数学，1984，6（2）：138－147.

［9］ 闵 杰，陈邦考.一种四次有理插值样条及其逼近性质［J］.高等学校计算数学学报，2007，29（1）：57－62.

［10］ Wang Qiang，Tan Jieqing.Rational quartic spline involving shape parameters［J］.Journal of Information and Computational Science，2004，1（1）：127－130.

［11］ Wang Qiang，Tan Jieqing.Shape preserving piecewise rational biquartic surface［J］.Journal of Information and Computational Science，2006，3（2）：295－302.

［12］ Duan Q，Djidjeli K，Price W G，et al.A rational cubic spline based on function values［J］.Computer and Graphics，1998，22（4）：479－486.

［13］ Bao Fangxun，Sun Qinghua，Duan Q.Point control of the interpolating curve with a rational cubic spline［J］.J Vis Commun Image R，2009，20：275－280.

［14］ Duan Q，Bao Fangxun，Du Shitian，et al.Local control of interpolating rational cubic spline curves［J］.Computer－Aided Design，2009，41：825－829.