基于相依函数型数据条件均值函数估计的渐近性质

丁 洁， 凌能祥

（合肥工业大学数学学院，安徽合肥 230009）

众所周知，条件均值函数的非参数估计是回归分析研究的重要问题，其理论与方法在经济、医学等领域中已有广泛的应用。条件均值函数的非参数估计中，通常解释变量X取值于Rd空间，响应变量Y取值于R1空间，（X，Y）的样本被认为是i.i.d或有某种相依的随机变量，文献［1－2］已取得一些有意义的成果。

近年来，随着计算技术的快速发展，在医学、经济学、环境计量学和计量化学等领域人们常常收集到曲线数据或函数型观察值。于是人们开始关注基于函数型数据的统计推断特别是非参数统计推断。关于函数型数据的详细背景及统计推断的早期工作参见文献［3－5］。最近，文献［6］利用Kolmogorov熵的原理和方法，进一步研究了基于函数型数据响应变量的条件均值函数、条件分布函数、条件密度函数和条件风险率函数的非参数估计，在i.i.d情形下获得了有关非参数估计量的几乎完全一致收敛性及其收敛速度。鉴于条件均值函数在金融中的广泛应用和时间序列问题的相依性，本文进一步利用Kolmogorov熵的原理和方法研究基于α混合相依函数型数据有关条件均值函数估计的几乎完全一致收敛性及收敛速度，推广现有文献中的相关结果。

首先简要介绍强相合的定义。过程｛（Xi，Yi），i≥1｝被称为强混合或α混合，如果

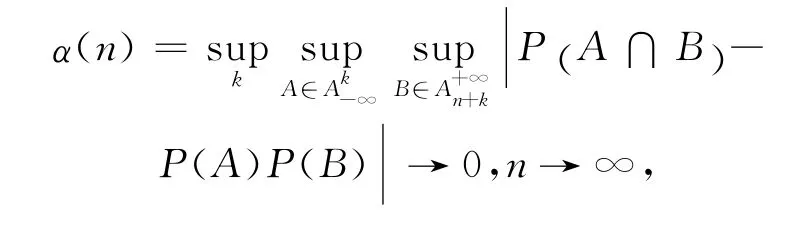
为了方便起见，本文中只假设｛（Xi，Yi），i≥1｝为算术α混合，且速度a＞1。

引进Kolmogorov熵的定义，设SF是半度量空间F的子集，给定ε＞0，如果这里B（xi，h）是以xi为中心的小球，半径h＞0，则F中有限个元x1，x2，…，xN称为SF的ε网点，当Nε（SF）是F中覆盖SF所需要的半径为ε的开球的最小个数时，（1）式称为SF的Kolmogorovε熵［7－9］，即

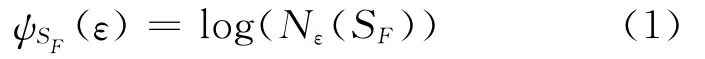
设｛（Xi，Yi），i≥1｝为同分布于（X，Y）的混合相依序列，其中X取值于有半度量d的抽象无限维空间（F，d），Y取值于R1空间。本文中，C、C′、C1为正常数，并在不同的情形下取不同的值。

根据文献［5］，定义条件均值函数（2）式的核估计如下，即

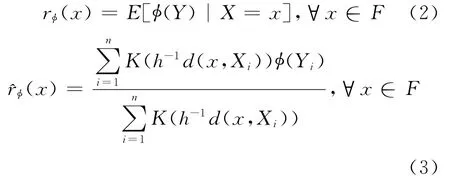
其中，K为核函数；φ（·）为已知实值Borel可测函数；窗宽

1 记号和假设

设SF为集合F的紧子集，记

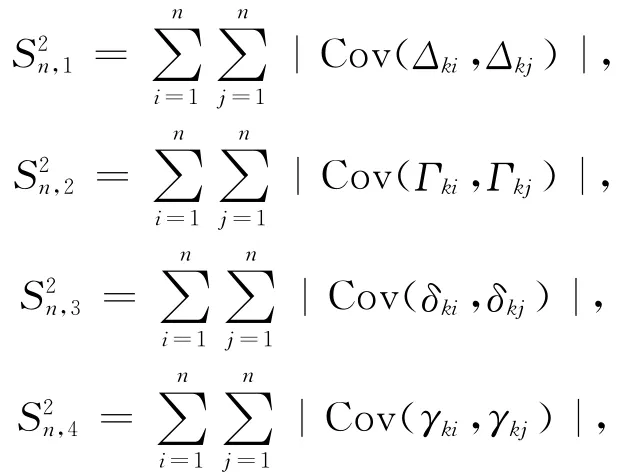
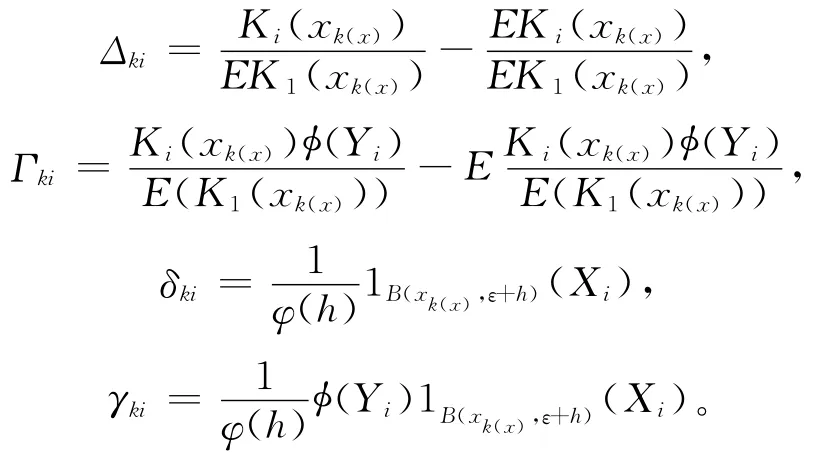
为得出本文主要结论，引入一些基本假设，关于回归函数r，假设条件如下：

H2 对于小球概率，设∀x∈SF，0＜Cφ（h）≤P（X∈B（x，h））≤C′φ（h），当h→0时，φ（h）→0。

H3 （nφ（h））＝O（logn）2。

H4 关于核函数，假设条件如下：核函数K（·）满足K（·）：R→R＋，且∫K＝1，支撑集为［0，1］。

H5 对于相依结构Sn，i，i＝1，2，3，4，存在θ＞C1β＋1＞2，使得：

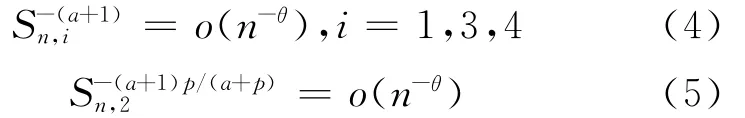
H6 假如如下：

其中，δm（·）在SF上连续。H1～H4为研究非参数函数型数据的渐近性的常用假设，参见文献［5］。与i.i.d场合相比，假设H5给出了相依结构在收敛速度方面的影响，这有助于给出有关收敛速度的一般性结论，需要特别指出的是，在假设H5中取C1＞1／β，并且C1取在假设H3、下面的H7成立的前提下，结论C1logn中的常数C1。最后，对于Kolmogorov熵，下面引用文献［6］中的假设。

2 引理及证明

2.1 引理

引理1 在假设H2～H5、H7下有：

其中

引理2 在假设H1、H2、H4下有：

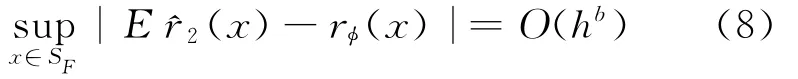
其中

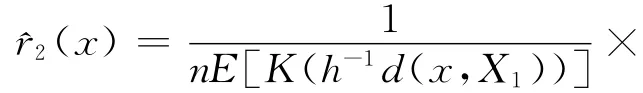
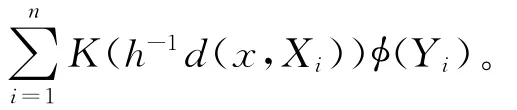
引理3 在引理1的条件下，对于某个给定的常数ε0，0＜ε0＜1，有

引理4 在假设H1～H7下，有

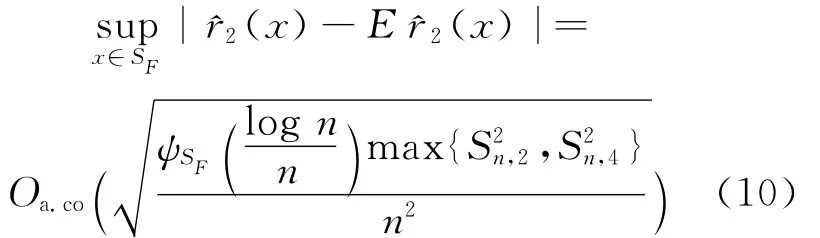
2.2 证明

（1）引理1的证明。根据文献［6］的分解，有

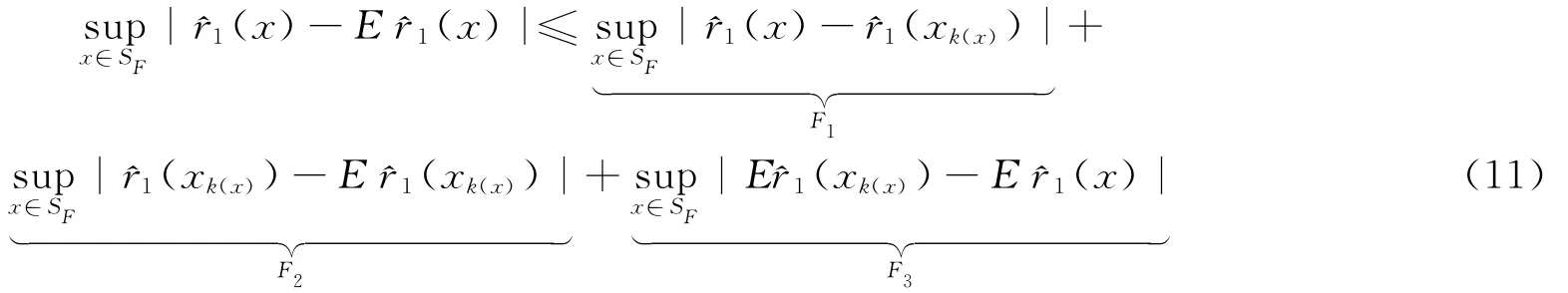
首先，研究F2，对于∀η＞0，有

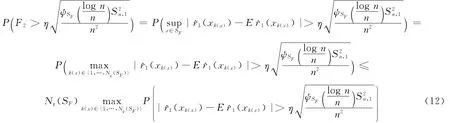
由文献［5］和Kolmogorov熵的定义，对于r＝log2n和某一个常数C＜∞，得

由（4）式，有

存在某个ε0＞0，获得并且取有

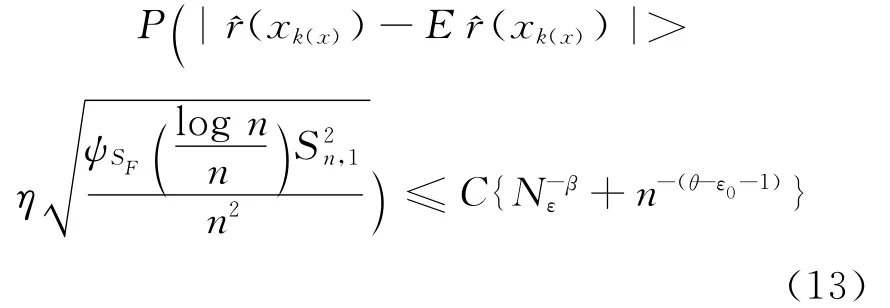
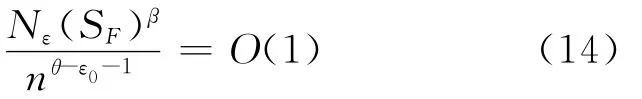
由（12）～（14）式以及假设H7，得

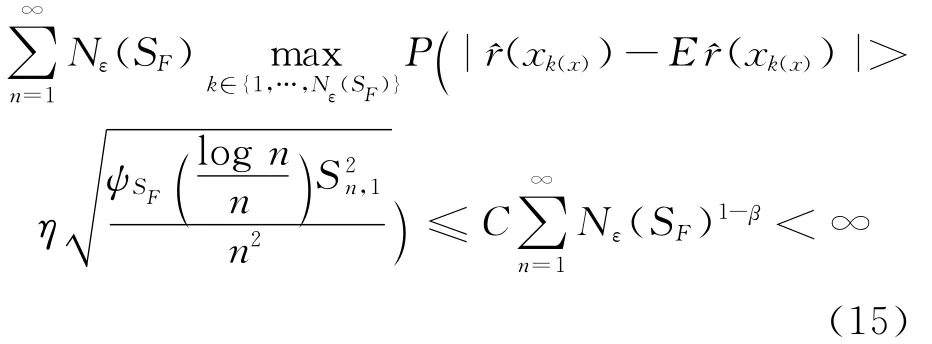
故有：

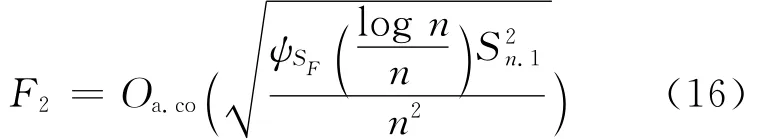
下面研究F1。根据＾r（x）的定义、核函数K的有界性以及上述k（x）的取法，关于F1可以得到下面的不等式：

类似于F2的证明，有

同理，有

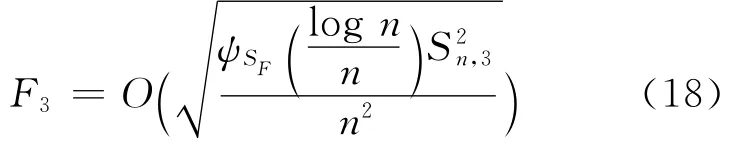
由（11）式以及（16）～（18）式，引理1得证。

（2）引理2的证明。类似于文献［6］中Lemma 10的证明。

（3）引理3的证明。由（7）式，结合文献［6］中Lemma 9的证明方法，此引理得证。

（4）引理4的证明。根据文献［6］中的分解方法，有

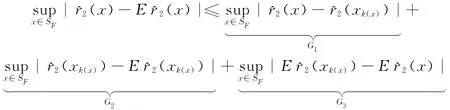
类似F1和F3的证明，可得：

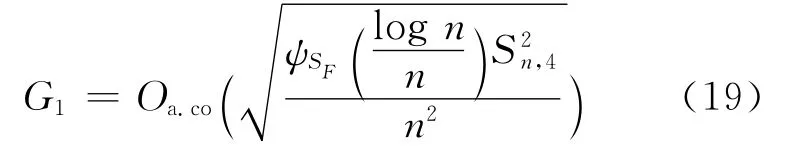
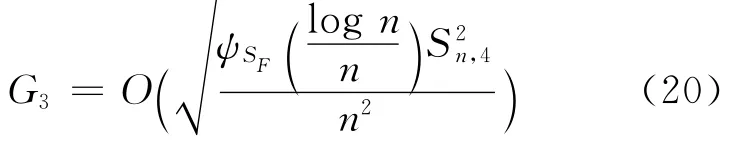
而对于G2，有

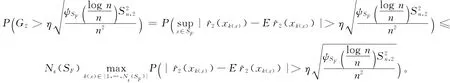
由（6）式以及Markov不等式，有

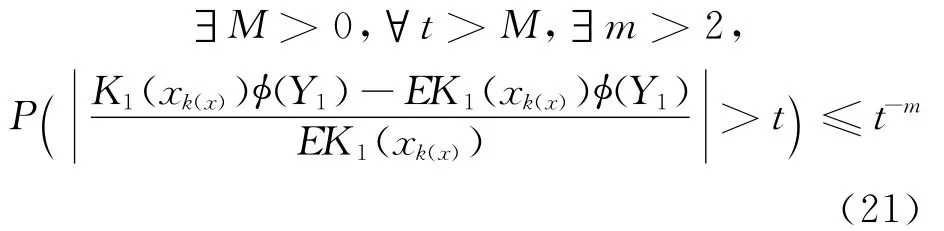
由（21）式和文献［5］，类似F2的证明，可得：

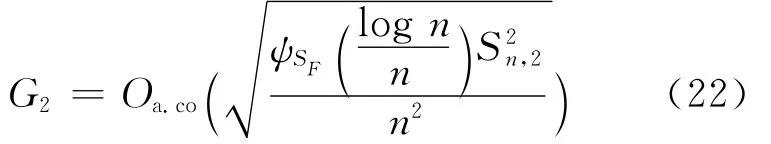
由（19）式、（20）式和（22）式，引理4得证。

3 主要结论及其证明

定理1 在假设H1～H7下，有

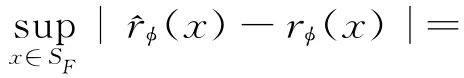
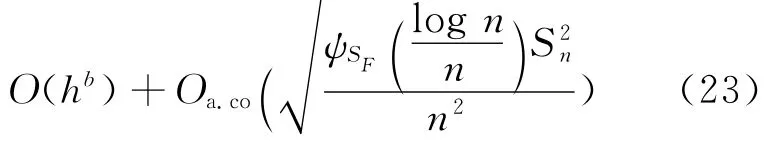
该结论给出了在相依函数型数据场合下估计量＾rφ（x）精确的一致收敛速度。这里收敛速度被分为2部分，第1部分和通常情形类似，只取决于回归函数的光滑参数算子，相依结构和熵对收敛速度的影响体现在第2部分。

证明 根据文献［5］，有如下分解：

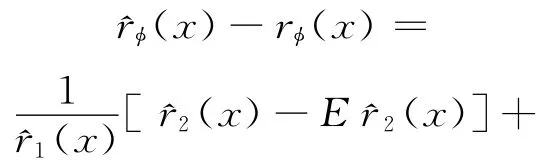
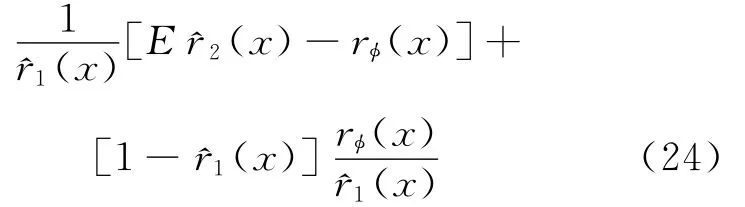
由上述4个引理的结论及文献［5］，定理得证。

［1］ Robinson R.Robust nonparametric autoregression［J］.Lecture Notes in Statistics，1984，26：247－255.

［2］ George G，Roussas R.Nonparametric regression estimation under mixing conditions［J］.Stochastic Processes and Their Applications，1990，36（1）：107－116.

［3］ Ramsay J O，Silverman B W.Functional data analysis［M］.New York：Springer，1997：5－50.

［4］ Ramasy J，Silverman B.Applied functional data analysis：methods and case studies［M］.New York：Springer，2002：10－50.

［5］ Ferraty F，Vieu P.Nonparametric funcional data analysis：theory and practice［M］.Berlin，Springer，2006：5－20.

［6］ Ferraty F，Laksaci A，Tadj A，et al.Rate of uniform consistency for nonparametric estimates with functional variables［J］.J of Statist Planning and Inference，2010，140（2）：335－352.

［7］ Kolmogorov A N，Tikhomirov V M.ε－entropy andε－capacity［J］.Uspekgi Mat.Nauk，1959，14：3－86.

［8］ Kuelbs J，Li W.Metric entropy and the small ball problem for Gaussian measures［J］.J Funct Anal，1993，116：133－157.

［9］ Theodoros N，Yannis G Y.Rates of convergence of estimate，Kolmogorov entropy and the dimensionality reduction principle in regression［J］.Ann Statist，1997，25（6）：2493－2511.