一种改进的OFDM系统定时同步算法

郭俊卿，陈云，胡俊

（1.重庆邮电大学通信与信息工程学院，重庆400065；2.山东电信潍坊分公司山东潍坊261041）

虽然OFDM有很多优点，但是它对时间和频率很敏感。因此，同步技术对于OFDM系统来说非常重要。在本文中，通过采用Kim等人提出的训练符号[1]，来产生脉冲式的定时度量，这样除了在正确的时间点外，其它点不会产生峰值。这种度量具有更高的准确性，并且比以前的方法性能更好。与其它算法不同，这种算法可以很容易的同时考虑时间和频率。本文改进的这种算法适用于多径衰落环境，并且可以很容易用CP或零填充。

1 系统建模

1）OFDM符号

在OFDM系统中，通常用等效基带来表示传输符号：

其中dn表示调制的数据符号，N表示子载波的个数。在有频率选择性多径衰落信道中，路径收益表示为{hm：m=0，1，…}，相应的路径延迟表示为{τm}，接收器接收的信号表示为：

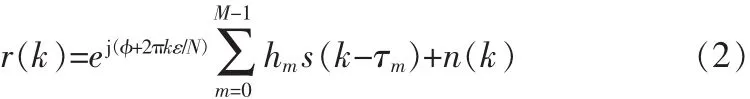
其中φ表示初始阶段，ε表示频率偏移，n（k）表示复杂的高斯噪声样值，并且均值为零样本方差为δ2n。

2）定时同步算法

时间同步确定了帧的起始位置。其中Schmidl提出的算法[2]，建议把训列符号两等分，并且使用相关性来确定帧的开始。使用一个PN序列，训练符号一般形式为[A A]，其中A表示长度为N/2的样值符号，Schmidl的定时估计算法显示帧开始的位置为下面时间度量的最大值：

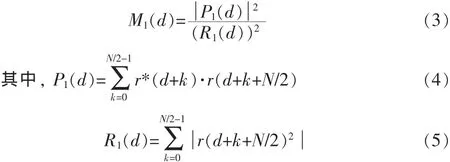
这种定时机制有一个大的缓冲期，降低了获得时间峰值的准确性。为了减少这种缓冲时间，Minn提出了一种算法[3]，这种算法有一个尖锐的峰值，但它仍然有很大的误差。相比较Minn的算法而言，Park提出的定时同步算法[4]，该算法有一个尖锐的峰值，并且方差要比Minn的小很多。Park算法用[AA*BB*]来表示一个训练符号，其中A是长度为N/4的样值符号，B与A是对称的，A*是A的共轭。这个定时度量通常表示为：

2 改进的符号定时同步算法

针对以上算法的缺点，本文提出了一种改进算法，改进算法采用Kim提出的训练符号序列[1]，它的形式为[AB*AB*]，其中A是训练序列符号长度的N/4，B与A对称，A*为A的共轭。这种改进的定时机制表示为:

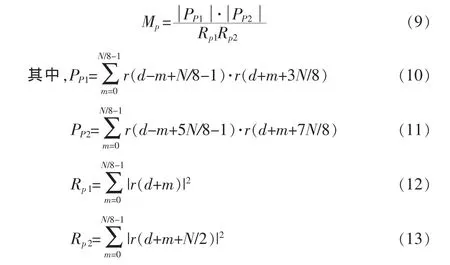
3 仿真结果分析

本文改进的同步算法通过计算机使用MATLAB工具来进行模拟仿真。考虑的条件是子载波N=1024和循环前缀CP=128时的OFDM系统。通常考虑两种信道条件下的仿真；一种是没有符号间干扰的AWGN信道，另一种是有符号间干扰的AWGN信道。本文建模为有随机延迟的16个信道，路径增益公表示如下：

本文的算法分别与Minn和Park等人的算法进行比较。图1显示了在AWGN信道中针对不同信噪比（SNR）条件下的定时均方误差（MSE）性能比较。当信噪比较小时，3种算法性能相当；但是，随着信噪比的增加，改进算法的性能优势逐渐明显；当信噪比达到15 dB以后，3种算法的MSE都趋于稳定。

图2显示了在ISI信道中针对不同信噪比（SNR）条件下的定时均方误差（MSE）性能比较。由于ISI的存在，相对于AWGN信道，定时均方误差整体有所增大；当信噪比超过20 dB时，改进算法的MSE有明显减小的趋势。由于改进算法的度量机制只产生一个峰值，这使得更容易把握正确的时间定时点，并且时间估计也更准确。从均方误差曲线上看，改进算法比Minn和Park的算法有更小的方差，并且改进算法适用AWGN信道和多衰落环境。

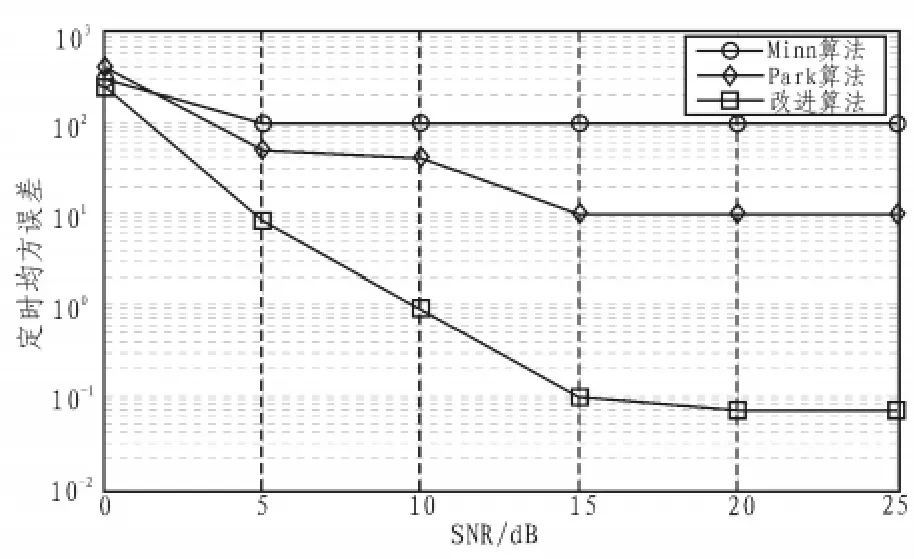
图1 AWGN信道中的定时MSE曲线Fig.1 Variance of timing offset estimator in AWGN channel

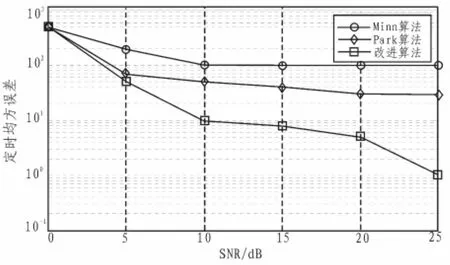
图2 ISI信道中的定时MSE曲线Fig.2 Variance of timing offset estimator in ISI channel

4 结论

本文通过与原有的定时同步算法比较，通过采用对称相关的性能，改进了原有的定时同步算法。改进算法可以很容易的同时兼顾时间和频域，并且改进算法中的定时度量消除了Schmidl算法中多余的峰值，与Park和Seung等人提出的算法中含有多个峰值不同，它只有一个正确的峰值。从仿真结果看，改进算法很明显比其它定时同步估计算法要好很多。在正确的定时点，它有很小的均方误差（MSE），适合AWGN和多衰落环境，并且容易用CP或零填充。因此，改进算法比较有利于在OFDM系统初始时刻进行同步，具有更高的精度和更好的性能。

[1]Kim J，Noh J，Chang K.Robust timing&frequency synchronization techniques for OFDM-FDMA systems[J].IEEE Workshop on Signal Processing Systems Design and Implementation，2005（11）：716-719.

[2]Schmidl T M，Cox D C.Robust frequency and timing synchronization for OFDM[J].IEEE Trans.Comm.，1997，45（12）:1613-1621.

[3]Minn H，Zeng M，Bhargava V K.On timing offset estimation for OFDM systems[J]IEEE Communication Letters，2000（4）:242-244.

[4]Park H S，Cheon H S，Kang C G，et al.A simple preamble for OFDM timing offset estimation[J].in Proc.of IEEE VTCFallv，2002（2）:24-28.

[5]Moose P H.A technique for orthogonal frequency division multiplexing frequency offset correction[J].IEEE Trans.Comm.，1994，42（10）:2908-2914.

[6]van de Beek J J，Sandell M，Borjesson P O.ML estimation of time and frequency offset in OFDM systems[J].IEEE Trans.Signal Processing，1997（43）:761-766.

[7]Seepedin E，Shi K.Coarse frame and carrier synchronization of OFDM systems:a new metric and comparision[J].IEEE Trans.on Wireless Communication，2004，3（4）:1271-1284.

[8]Choi S D，Choi J M，Lee J H.An initial timing offset estimation method for OFDM systems in rayleigh fading channel[C]//64th IEEE Vehicular Technology Conference VTC-2006 Fall，2006:1-5.