基于改进AHP算法的某武器质量评估研究

倪小刚，曹菲，宋洪军

（1.第二炮兵工程学院101教研室，陕西西安710025；2.第二炮兵士官学校基础部计算机教研室，山东青州262500）

在当今世界各国争相研制和发展高、精、尖武器装备的激烈竞争环境下，武器系统的质量评估作为一项不容忽视的问题，得到日益广泛和深入地研究。许多新式武器定型后刚开始服役于部队，有限的可靠性数据也多出自生产单位，在一定程度上制约了部队对该产品实施最终地管理、使用和维护措施，迫切需要新的方法对其进行深入细致地研究[1]。

武器系统是一个多因素的复杂系统，包含多种不确定因素，如数据匮乏、信息不明确、主观判断定义不明确等。对这样一个不可知或不确定因素较多的复杂系统，传统的效能评估方法基于海量数据，缺乏基于系统内层“微观”描述模型的支持，很难有效的对系统实施科学可信的评估。

本文提出了一种质量评估的改进算法：基于层次分析的神经网络算法（AHP-BP算法）。即在历史的数据的基础上，以层次分析法和指数分析法所得到的系统性能指数作为BP神经网络输出层，以量化数据作为输入层样本，通过有限的导师训练方式，达到理想网络模式。AHP-BP算法具有运算速度快，精度高优点，为小样本，贫信息的评估问题提供了可行的数学分析工具。实践证明，采用这种评估方法进行武器系统的质量评估是合理可行的。

1 武器质量评估指标体系确定

1.1 武器质量评估指标原则

武器系统的质量评估是其战术技术性能的综合表征，由于指标受一些条件的影响，在质量评估方面存在着许多不确定因素，具有一定的模糊性，体系的确立原则：1）评价指标必须与目标密切相关；2）评价指标应能全面反映评价对象的各个方面；3）指标总数应尽可能少；4）指标数据应具有可得性。

武器系统庞大，结构复杂，影响其质量状况的因素繁多，武器的质量评估在作战指挥与作战运用中具有十分重要的意义，根据某武器系统所担负的任务和特点，并结合影响质量评估的主要因素，按照指标体系最简性、可测性、完备性、可比性和独立性原则[2]，建立如图1所示的武器系统效能三级评价指标体系。

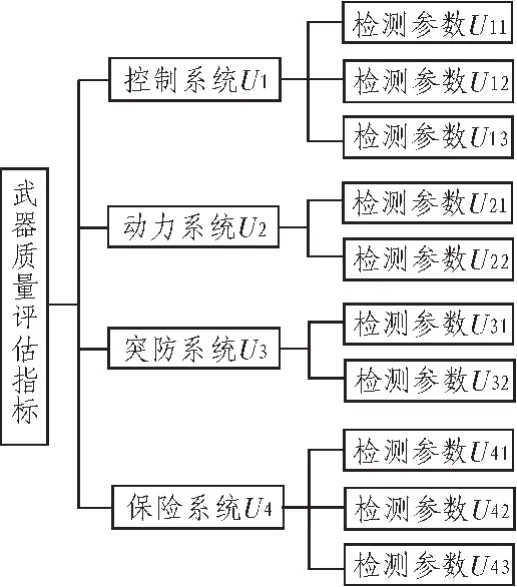
图1 系统总体质量评估递阶模型Fig.1 Evaluation step-down model of whole quality

1.2 武器系统性能指数

在军事问题的研究中，指数法可以用来反映诸多人员和武器在一定条件下相对平均的能力，根据指数法效能评估的思想，引入数据质量指数和系统性能指数概念，比较适合本系统特点。

2 AHP-BP算法的基本步骤

2.1 构造层次模型的权重判断矩阵

对于三层指标结构，存在两种类型的判断矩阵，目标—准则判断矩阵和准则—措施判断矩阵。目标—准则判断矩阵主要用于计算准则层的各个指标的相对权重，则准则—措施判断矩阵主要用于计算某准则下的各个措施层指标之间的相对权重。两类判断矩阵的形式相同，只是层次不同。具体形式如下：

式中ai，j表示ai指标相对于aj指标的相对权重。

2.2 权重系数的确定

层次分析法的指标权重计算问题，可以归结为判断矩阵的特征向量和最大特征值的计算，主要有方根法、和积法、幂法等，方根法的计算步骤如下：

步骤1，计算判断矩阵A的每一行元素的乘积，

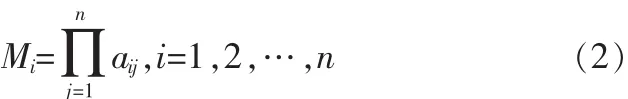
步骤2，计算的次方根，

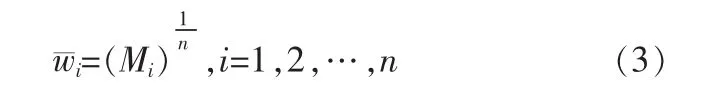
步骤3，对进行归一化处理，

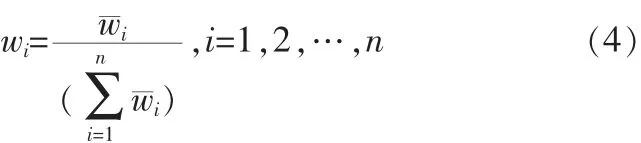
则所求权向量w=[w1，w2，…，wn]T。

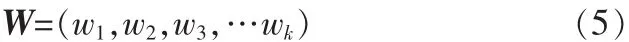
设依据上述方法求得的目标准则层权向量为wi为准则层指标在准则层中所占的相对权重。

设对于第k个准则层指标，各个准则下的措施层指标权重为

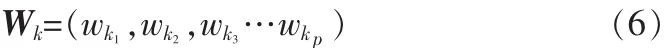
则层次结构中，准则i下的措施j指标的综合权重计算为

2.3 求解数据质量指数数学模型的确定

测试数据的质量指数算法一般以当前试值为基础测通过适当模型计算该参数的无量纲化评估值，该评估值反映了各项要素的实际量值满足需求的程度。Eθ为数据质量指数x为测量数据。根据该武器系统标准参数要求的特点，采用如下模型估算[3]:

1）直线模型

参数有上限要求，且参数越逼近上限时质量状态越差，采用直线型模型:

式中:x0为误差上限。

2）折线型模型

当某部件的测试数据要求界于某一范围之内，那么在该区间内其测试结果的变化对部件质量的影响是不一样的，如果参数处于边限附近时质量状态较差，采用折线型模型:

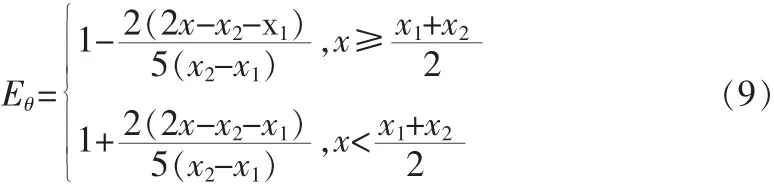
式中:x为性能参数的测试结果；x1为部件测试参数的最小允许值；x2为部件测试参数的最大允许值。

3）升半柯西分布模型

参数有下限要求，且实测值越小时质量状态越差，采用升半柯西分布模型:

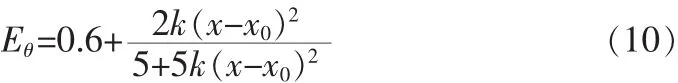
式中:k为常数，x0为误差下限；

2.4 求解系统性能指数模型的确定

加权和法模型，权重系数的作用较为明显，合成结果突出了量值较大和权重系数值较大的指标的作用；而加权积法模型，权重系数作用不太明显，但当某一项子要素的质量指数出现0值时，其综合评估结果为0，指标间的不可补偿特性作用明显。考虑到武器质量评估指标体系中的各指标间有的存在补偿性，有的没有可补偿性，权重系数在各个指标间的不均衡[4]，综合应用加权和法与加权积法，构造如下加乘混合模型计算系统性能指数。

2.5 BP神经网络的学习训练

BP算法是神经网络学习中应用最广、发展最迅速的学习算法[5]，它克服了人为主观因素和线性神经网络的局限性，可以实现任意线性或非线性的函数映射。本文采用以历史数据质量指数作为网络输入层，系统性能指数作为输出层的三层BP神经网络，该数学模型使有限的历史数据得到充分利用，有效克服了精确率在质量评估的瓶颈。具有精度高，速度快的优点。程序流程如图2所示。

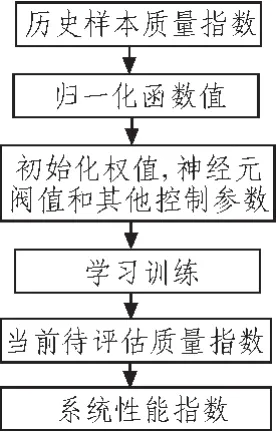
图2 算法流程图Fig.2 Flow chartofarithmetic

隐层神经元个数的确定始终是BP算法的一个难点问题。隐层神经元的个数太少，则BP网络的认知能力较差，影响其收敛程度和泛化能力；隐层神经元的数量太多，将会使计算量增加，影响BP网络的收敛速度。基于样本数据相对短缺的实际[6]，综合考虑输出层神经元数和输入层神经元数，提出了一种计算隐层神经元数的公式：

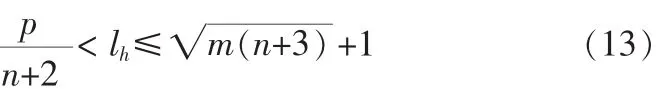
式中：lh表示隐层神经元数，n表示输入层的神经元数，m表示输出层的神经元数，p表示样本总数。

3 实例分析

在质量评估之前，首先用历史数据对上述的性能评估系统进行辨识，输入层、隐含层和输出层的结点数分别为10×4×1，激活函数采用Sigmoid型，学习率η=0.9，学习训练算法采用反向传播（BP）算法，目标误差为0.001。一旦神经网络训练完毕，便可成为一种有效的工具，去评价系统性能Q。

某型武器定期检测，某次检测数据量化指标如下，分析其系统性能。

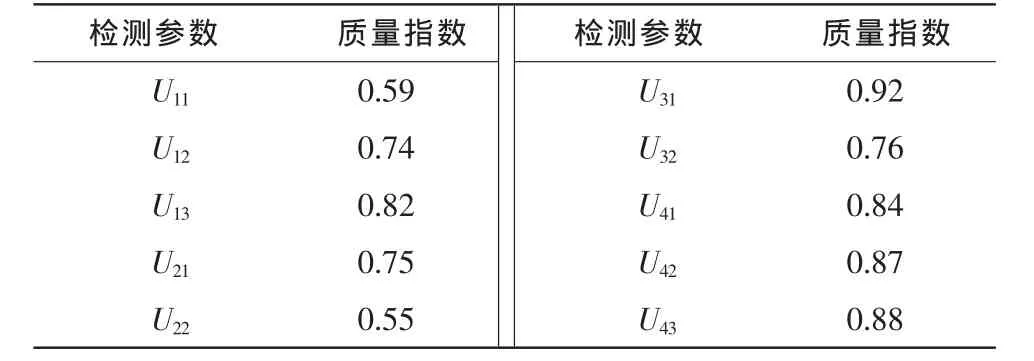
表1 某武器系统性能量化指标Tab.1 Chemical composition of experimental alloy

1）建立指标体系。

2）构造判断矩阵，计算权重系数。依据判断矩阵，可以得到相应的权向量：

W=（0.090 5 0.152 3 0.313 6 0.443 6）W1=（0.35 0.45 0.20）W2=（0.57 0.43）W3=（0.55 0.45）W4=（0.15 0.55 0.30）进而可得每个指标的权值。

3）计算系统性能指数。根据式（12）可得，Q′=0.768 1。而应用本文提出的AHP-BP算法，将表1中的指标质量指数作为BP神经网络输入层，输出层可得到系统性能指数Q=0.852 3。

4）分析质量评估结果。在实际检测过程中，U11和U22指数偏低是由于系统某保险解除后，系统负载增多造成的，属于正常，不影响系统效能。结果显示传统的层次分析法容易受某个指标质量指数（如U11，U22）影响，不能贴近实际，从而得到不太理想的性能指标，而AHP-BP算法训练的神经网络具有良好的联想和容错能力，仿真结果符合实际，从而检验了AHP-BP算法的有效性。

4 结论

采用层次分析的神经网络算法对装备质量进行评估是人工神经网络理论[7]在质量评估方面的一次尝试，结果表明该方法有效可行，而且其泛化能力使它可以无需作较大修改，便可以应用于其它武器系统的质量评估，省去了建立解析模型的大量工作，为准确、快捷地估算新装备质量效能提供了一种新思路。

[1]张杰，唐宏，苏凯，等.效能评估方法研究[M].北京:国防工业出版社，2009:50-55.

[2]时俊红.武器系统效能评估方法浅论[J].火控雷达技术，2003，32（4）:47-49.

SHI Jun-hong.Commentson methods for evaluating weapon system effectiveness[J].Fire Control Radar Technology，2003，32（4）:47-49.

[3]刘伟，杨世荣，李小强.地地导弹质量评估方法研究[J].弹箭与制导学报，2006，26（2）:35-37.

LIU Wei，YANG Shi-rong，LI Xiao-qiang.Evaluation method study on the quality of surface to surface missile[J].Journal of Projectiles，Rockets，Missiles and Guidance，2006，26（2）:35-37.

[4]张西川，杨丽娜，袁大天，等.机载C3I系统试飞数据质量评估方法[J].火力与指挥控制，2009，34（6）:8-10.

ZHANG Xi-chuan，YANG Li-na，YUAN Da-tian，et al.Research on data quality evaluation methodology on the flight-testing of the plane-carried C3I system[J].Fire Control&Command Control，2009，34（6）:8-10.

[5]原慧琴，杨文伟.BP算法在网络性能评估中的应用[J].现代计算机2006，（247）:34-36.

YUAN Hui-qin，YANG Wen-wei.The application of BP algorithm to the function evaluation of network[J].Modern Computer 2006，（247）:34-36.

[6]杨峰，王维平.武器装备作战效能仿真与评估[M].北京:电子工业出版社，2010:76-88.

[7]唐德翠.基于改进BP神经网络的纸浆漂白MIMO软测量模型研究[J].工业仪表与自动化装置，2009（3）：54-56.

TANG De-cui.Research on soft measurement model of paper bleaching processbased on improved BP neural network[J].Industrial Instrumentation&Automation，2009（3）：54-56.