基于LMS自适应滤波器的设计

姜泉璐，汪立新，吕永佳，吴玉彬，叶军

（第二炮兵工程学院陕西西安710025）

为消除惯组时间序列的插值和预测分析中带入的一些误差，最好的方法就是用惯组已有的测试数据对预报结果做一些处理，以使预报结果更能反映惯组的实际状况，为此，滤波是一种改善预测结果的有效方法。

滤波的方法很多，如卡尔曼滤波、维纳滤波、自适应滤波等。维纳滤波器参数是固定的，适用于平稳随机信号[1]。卡尔曼滤波参数是时变的，适用于非平稳随机信号[2]，这两种滤波器只有对信号和噪声的统计特性先验已知的情况下，才能获得最优滤波。然而在实际应用中，常常无法得到这些统计特性的先验知识，或者，统计特性是随时间变化的。因此，用维纳滤波或卡尔曼滤波器实现不了最优滤波，在这种情况下，自适应滤波能够提供卓越的滤波性能[3]。自适应滤波可以根据以前的测试结果通过加权来修正现在的结果，这正适合对插值产生的时间序列的预报结果进行修正，修正由插值带来的误差。因此自适应滤波是对惯组测试参数时间序列预报结果进行修正的理想方法。

1 基本LMS算法

自适应线性组合器是构成自适应数字滤波器的基本部件。令W（n）表示图1中的权系数向量，W（n）=[w1（n），w2（n），…，wM（n）]T，设线性组合器的M个输入为X（k-1），X（k-m）即

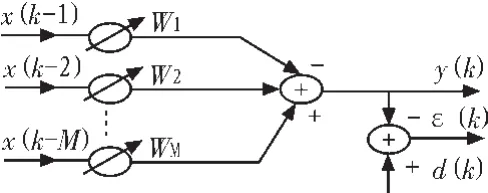
图1 自适应线性组合器Fig.1 Adaptive linear combination

X（n）=[x（n），x（n-1），…，x（n-m）]T，其输出y（k）是这些输入加权后的线性组合，即

如图1所示，令d（k）代表“所期望的响应”，并定义误差信号

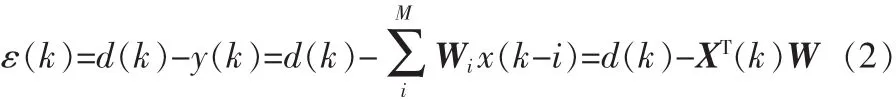
式（2）平方为

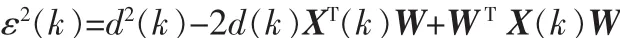
上式两边取数学期望后，得均方误差

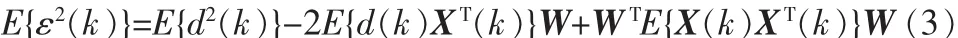
定义互相关函数行向量RTXd=E{d（k）XT（k）}和自相关函数矩阵RTXX=E{X（k）XT（k）}，则均方误差（3）可表示为：

这表明，均方误差是权系数向量W的二次函数，它是一个中间向上凹的抛物型曲面，是具有唯一最小值的函数。调节权系数使均方误差为最小，相当于沿抛物型曲面下降找最小值。

将式（4）对权系数W求导数，得到均方误差函数的梯度

令（k）=0，即可求出最佳权系数向量

它恰好就是著名的Wiener-Hoof方程。因此，最佳权系数向量Wopt通常也叫Wiener权系数向量。将Wopt代入式（4），得最小均方误差

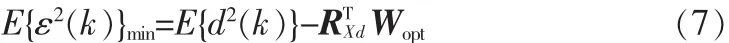
利用式（6）求最佳权系数向量的精确解需要知道RXX和RXd的先验统计知识，而且还需要进行矩阵求逆等运算。Widrow and Hoff（1960）提出了一种在这些先验知识未知时求Wopt的近似值的方法。习惯上称之为Widrow-Hoff LMS算法。这种算法的根据是最优化方法中的最速下降法。根据最速下降法，“下一时刻”权系数向量W（k+1）应该等于“现时刻”权系数向量W（k）加上一个负均方误差梯度-Δ（k）的比例项，即

W（k+1）=W（k）-μΔ（k）（8）

式中，μ是一个控制收敛速度与稳定性的常数，称之为收敛因子。

不难看出，LMS算法有两个关键：梯度Δ（k）的计算以及收敛因子μ的选择。

2 Δ（k）的近似计算

精确计算梯度Δ（k）是十分困难的。根据文献[5]，一种粗略的但是却十分有效的计算Δ（k）的近似方法是：直接取ε2（k）作为均方误差的估计值，即

于是，Widrow-Hoff LMS算法最终为

如图2所示。

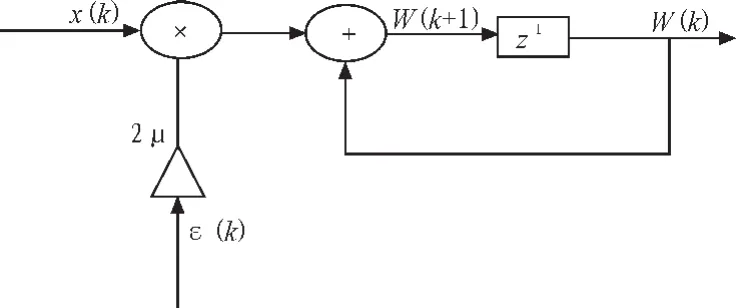
图2 LMS算法的方框图Fig.2 Block diagrams of LMS algorithm

下面分析梯度估值Δ(（k）的无偏性。Δ(（k）的数学期望为

在上面的推导过程中，利用了d（k）和ε（k）皆为标量的事实。在得到最后的结果时，利用了式（5）。式（11）表明，梯度估值（k）是无偏估计。

3 参数μ的选择方法[6-7]

对权系数向量更新公式（10）两边取数学期望，得

式中，I为单位阵。

当k=0时，E{W（1）}=（I-2μRXX）E{W（0）}+2μRXd。

对于k=1，利用上式结果，有

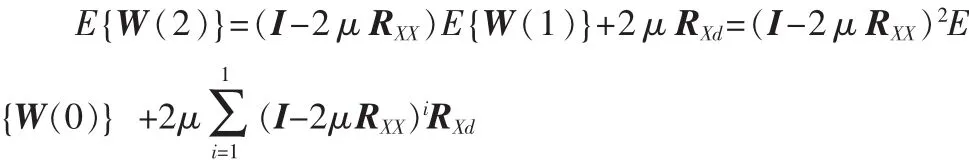
起始时，E{W（0）}=W（0）。

重复以上迭代至次k+1，则有

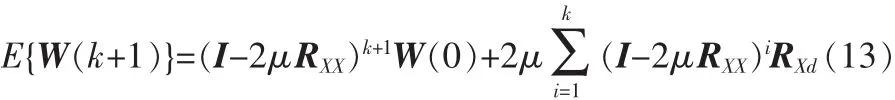
由于RXX是实值的对称阵，可以写出其特征值分解式

这里，利用了正定阵Q的性质Q-1=QT，且Σ=diag（λ1，…，λM）是对称阵，其对角元素λi是RXX的特征值。将式（14）代入式（13）后得

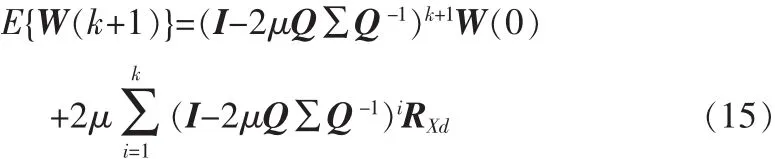
注意到以下恒等式及关系式：

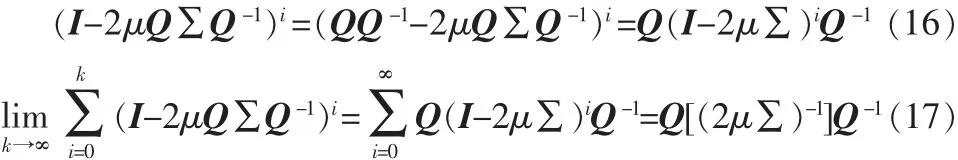
假定所有的对角元素的值均小于1（这可以通过适当选择μ实现），则

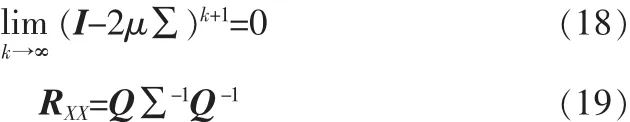
将式（16）～（19）代入式（15），结果有

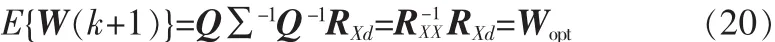
由此可见，当迭代次数无限增加时，权系数向量的数学期望可收敛至Wiener解，其条件是（I-2μΣ）对角阵的所有对角元素小于1，即

或

其中λmax是RXX的最大特征值。μ称为收敛因子，它决定达到式（13）的速率。事实上，W（k）收敛于Wopt由比值d=λmax/λmin决定。

算法1列出了基本的LMS自适应算法，而LMS自适应滤波器如图3所示。

图3 LMS自适应滤波器Fig.3 Adaptive filter of LMS

算法1（基本LMS自适应算法）：初始化：

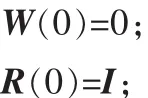
k=1→n循环做下式：

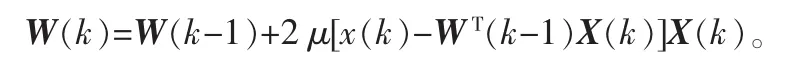
4 应用举例

4阶AR模型为：

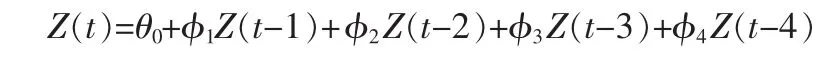
由文献[4]的插值结果为样本可求得：

预测及滤波结果如图4所示。

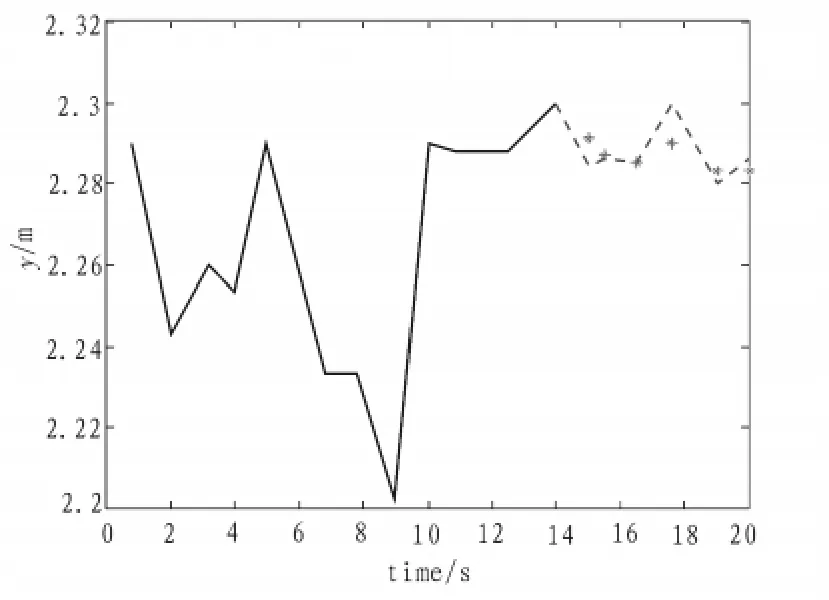
图4 预测及滤波结果Fig.4 Result of prediction and filter

图中实线（前14次）为标定结果，虚线（后6次）为预测结果，星号为滤波结果。

预测结果的检验如表1所示。

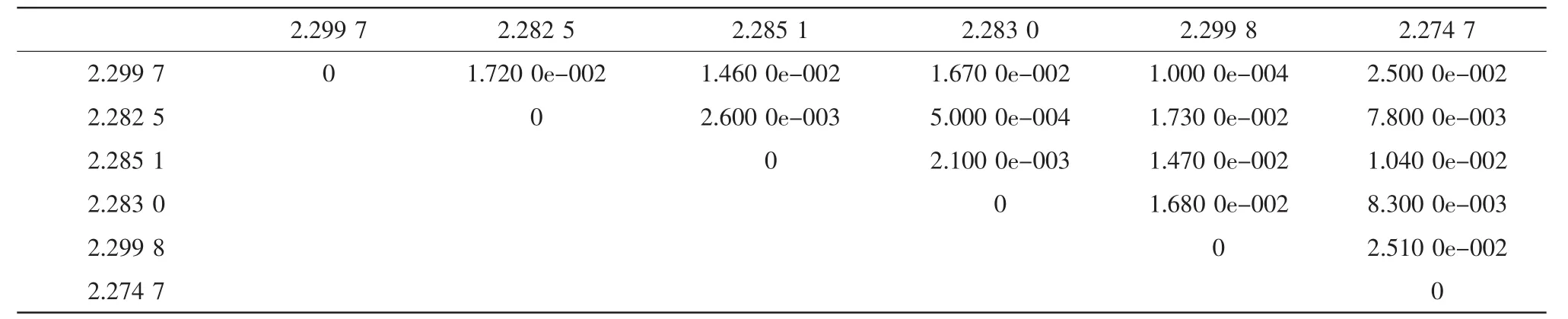
表1 预测结果Tab.1 Result of prediction

此误差系数的合格性标准和准确性标准分别为：≤4，≤0.45。可以看到表1中的数据完全通过了准确性和稳定性检验，即对此误差系数的预测是有效的。

5 结论

针对在惯组时间序列的插值和预测分析中，不可避免会引入一些误差的特点，设计了一种基于LMS自适应滤波器，该滤波器不仅能够自动地调节现时刻滤波器参数，适应信号和噪声未知的或随时间变化的统计特性，而且可根据以前的测试结果通过加权来修正现在的结果，对插值产生的时间序列的预报结果进行修正，最终实现最优滤波。仿真结果表明该方法是对惯组测试参数时间序列预报结果进行修正的有效方法。

[1]Nebot E，Durrant-Whyte H.Initial calibration and alignment of low-cost inertial navigation units for land vehicle applications[J].Journal of Robotic Systems，1999，16（2）:81-92.

[2]Muller K R，Smola A J，Ratsch G，et al.Predicting time series with support vector machines[C].//Lecture Notes in Computer Science，1997:999-1004.

[3]邓乃扬，田英杰.数据挖掘中的新方法支持向量机[M].北京：科学出版社，2004.

[4]钟万登.液浮惯性器件[M].北京:宇航出版社，1992.

[5]尉询楷，李应红，张朴，等.基于支持向量机的时间序列预测模型分析与应用[J].系统工程与电子技术，2005，27（3）:529-532.

WEI Xun-kai，LI Ying-hong，ZHANG Pu，et al.Analysis and applications of time series forecasting model via support vector machines[J].Systems Engineering and Electronics，2005，27（3）:529-532.

[6]徐军辉.联惯性测量组合数据分析方法研究[D].西安:第二炮兵工程学院，2003.

[7]周刚.稳定性检验方法研究[D].北京：国防大学，1994.