航空深弹投放模型及空中弹道仿真
2011-03-24陶万成杨日杰徐景峰
陶万成,杨日杰,熊 雄,徐景峰
(1.海军航空工程学院电子信息工程系,山东 烟台 264001;2.海军潜艇学院,山东 青岛 266071)
无动力航空自导深弹是由反潜直升机携带专门用以攻击潜艇的一种水中兵器。除具有传统深弹结构简单、制造容易、价格低廉、便于批量生产和装备、可靠性高、不受水文条件限制等优点外,增加了自导捕获和跟踪目标潜艇装置,使其攻潜效果与传统深弹相比有了大幅度的提高,因此受到各国的重视。尽管国内针对深弹攻潜效能做了大量相关研究,但很多是关于普通深弹的[1-2],而且主要是围绕深弹命中潜艇的概率[3-6]展开的,没有结合反潜直升机应召攻潜航路考虑深弹的投放问题,没有考虑海洋战场环境因素对深弹空中弹道及入水参数的影响,而深弹投放时机、位置及入水参数对攻潜效能的影响是不能低估的。因此,对航空自导深弹投放及空中弹道研究是十分有意义的。
1 反潜直升机使用自导深弹应召攻潜战斗过程描述
本文假定潜艇运动要素已知且潜艇是定速直航的,直升机根据本身的飞行参数和海洋环境因素应召飞往潜艇预测位置,在投弹点投放航空自导深弹对潜攻击。
反潜直升机应召攻潜航路规划模型:以正东方向为x轴,正北方向为y轴建立坐标系;已知反潜直升机升空后的位置坐标 A(xa,ya),航速为vhel,航向与x轴夹角为β,风速 vwind,风向与x轴夹角为α,合成速度为vreal,见图1;潜艇初始位置 S (xs,ys),航速 vm,航向与x轴夹角为θ,反潜直升机的最大转弯坡度为ω。
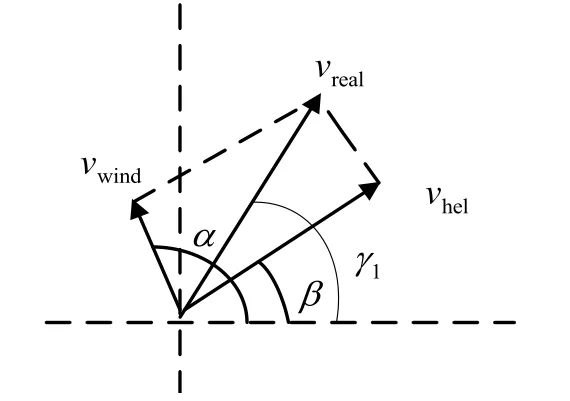
图1 合成速度示意图
反潜直升机应召飞往潜艇预测位置的过程可分为协调转弯和以提前角ϕ 向目标直飞2个阶段。
在转弯过程中任意点的速度应满足:

转弯过程中任意点的位置(x (t),y (t))满足:
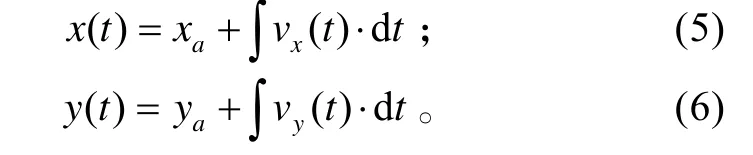
设转弯时间为tz直升机飞到B点时转弯结束,此时潜艇位置为S1(xs,ys):
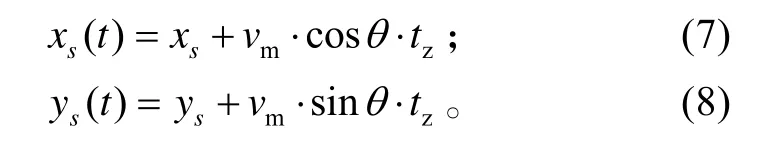
此后直升机开始以提前角ϕ 飞往目标区域,在经过时间 tf后达到攻击点,准备投弹发起攻击。

式中:m为潜艇与飞机速度比;mQ为直升机在B点时的目标弦角。由相遇三角形及余弦定理解出 tf。
2 直升机投放深弹攻潜过程
2.1 深弹攻击命中原理及参数解算模型
以正北方向为y轴,正东方向为x轴,建立如图2所示的坐标系:O为直升机悬停点;M0为目标初始位置;T为直升机投弹点;Mq为深弹与目标相遇点;D0为目标初始距离(m);Cm为目标航向(°);B0为目标方位(°);Q0为目标弦角(°);ϑ0为命中角(°);HFC为应飞航向(°);tf为应飞时间(s);td为深弹工作时间(t1+t2+t3)(s);vf为直升机速度(m/s);vm为目标速度(m/s);A=TMq为深弹下落水平距离(m)。

图2 深弹投放命中原理
当直升机获取目标速度、航向后,就可根据直升机本身的飞行参数和深弹的空中弹道和水下弹道,选择前飞航向和飞行时间,在T点投弹,深弹经过空中下落时间1t、水下减速段 t2的过渡和极限速度下沉段3t的垂直下沉与潜艇相遇。因为本文研究的是一种无动力自导深弹[6],它被投放后。经过空中的开伞减速降落入水,经过短暂的入水过渡段,自导头开始工作,当发现目标后,打舵导向目标爆炸,毁伤潜艇。
由图2分析解算得:

应飞时间

式中:
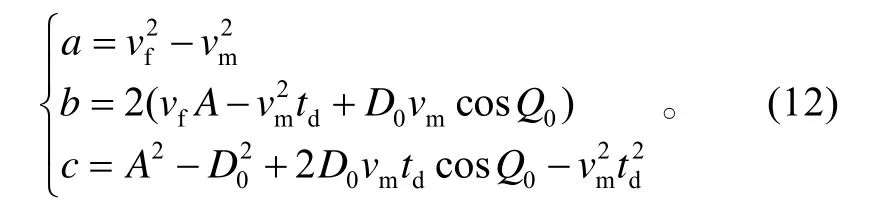

Mq点的坐标 (XMq,YMq)可表示为:
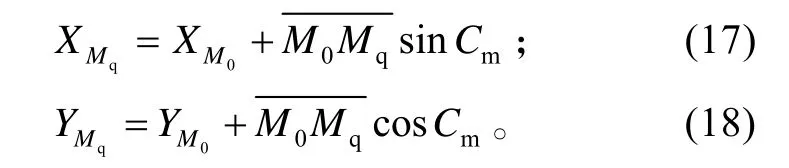
应飞航向:
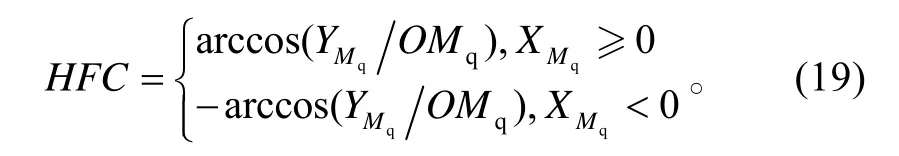
2.2 深弹投放间隔选择
投弹间隔是深弹使用中必须考虑的一个战术参数。反潜直升机使用航空自导深弹攻潜时一般采用连投的方法。由于直升机连投深弹的时间很短。可认为深弹是同时入水,可将数枚深弹作用和爆炸的范围视为一长方体,如图3所示,只要潜艇在此长方形覆盖带内,潜艇就被命中。
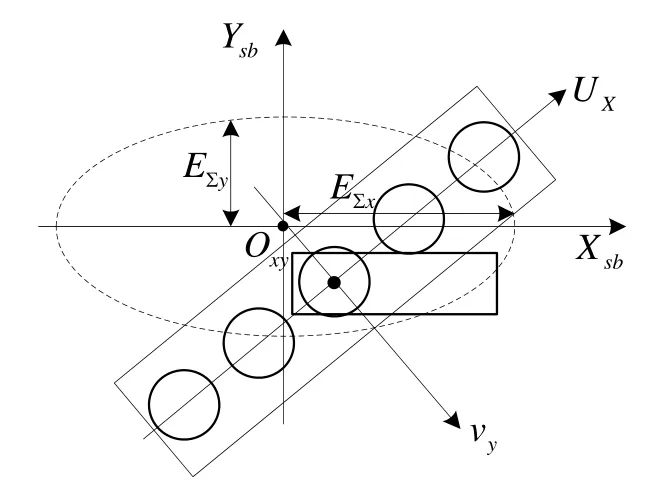
图3 连投命中目标示意图
当反潜直升机使用深弹连投攻击目标时,其投弹间隔的大小与深弹的作用范围有关。对于无动力自导深弹来说,文献[6]给出了一种计算投弹间隔的方法,如图4所示。
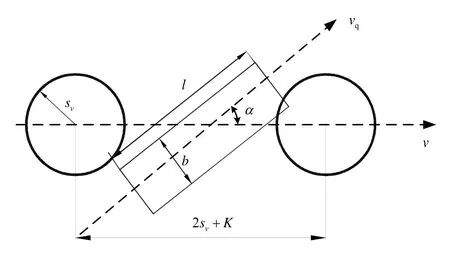
图4 投弹间隔示意图
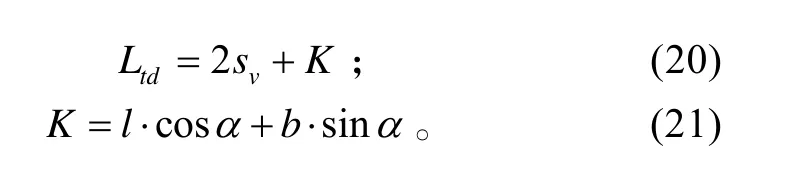
式(20)、(21)中:Ltd为投弹间隔;l和b分别为潜艇等效长度和宽度;α为潜艇运动方向与投弹线的夹角(攻击进入角),该角度还表示出了潜艇的航向;vs为深弹在目标深度上自导作用范围的水平投影,

式(22)中:0h为入水过渡深度;bR为深弹破坏半径;h为深弹实际下沉深度;hmax为海区最大深度;d为深弹自导装置发现目标的距离;γ为深弹最大下滑角。
由式(20)~(22)可知,投弹间隔的大小与深弹作用范围和目标尺寸有关,一般目标尺寸假定不变,而深弹作用范围与其工作深度有关,深度的选择取决于海区深度和潜艇所在深度。因此,航空自导深弹投弹间隔的选取主要取决于使用海深,即浅水使用,投弹间隔要小;深水使用,投弹间隔要大。其间隔设定可参考表1。

表1 海深与深弹自导作用范围及投弹间隔关系表
3 航空深弹空中弹道模型
3.1 空中弹道数学模型
为得到深弹入水参数,有必要对深弹的空中下落过程进行仿真分析。为研究问题方便,暂不考虑深弹的横滚,由于降落伞和深弹所组成的系统(简称“伞弹系统”)的运动在垂直面内,因此仅建立弹伞系统的纵向运动方程。由受力分析知,弹伞系统在空中仅受重力、升力和阻力,由此得到弹伞系统运动的简化数学模型[7]:

式(23)~(29)中:Θ为深弹弹道倾角;ω为深弹的角速度;A为深弹阻力系数;l为伞悬点距离深弹重心的距离;J为转动惯量;Mzα为作用在深弹上的气动力矩;Yα为升力系数;m为深弹质量;K为降落伞的阻力系数;α为深弹攻角。
3.2 空中弹道Simulink仿真模型
由“伞弹系统”的空中弹道数学模型,利用Matlab/simulink 软件建立相应的Simulink模型[8](如图5所示)进行相关参数设置,然后计算“伞弹系统”的速度、弹道倾角和角速度,得出伞弹系统的空中弹道轨迹及入水角、攻角等相关入水参数。其中,入水角是深弹入水时深弹弹轴与水平面所成的角;攻角是深弹速度方向在弹体坐标系[9]中的投影与深弹弹轴的夹角。
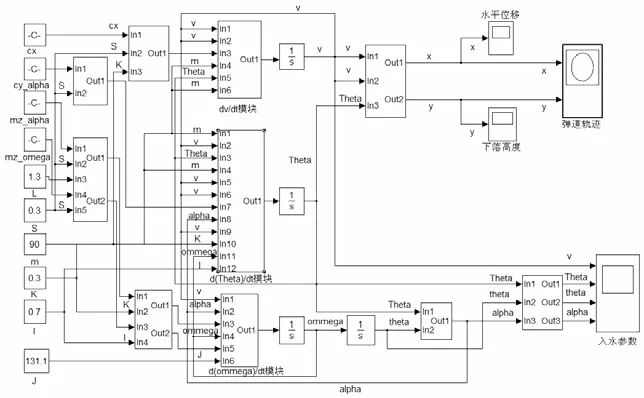
图5 空中弹道Simulink仿真模型
4 仿真结果分析
4.1 投弹速度对入水角的影响
图6给出了当投弹高度为200 m时直升机分别以100 km/h、150 km/h、200 km/h、250 km/h的速度投弹时入水角随时间变化的曲线。由图6可以看出,投弹速度对深弹入水角的影响主要集中在投放后的2~4 s,同时,投弹速度变大,入水角变化趋于平缓,有利于提高深弹入水的稳定性。

图6 投弹速度对入水角的影响
4.2 投弹速度对弹道攻角的影响
图7给出了当投弹高度为100 m时直升机分别以100 km/h、150 km/h、200 km/h的速度投弹时俯仰角随时间变化的曲线。由图7可知直升机投弹瞬间攻角为0,随着深弹下落形成正攻角,随后降落伞展开,开伞扰动攻角明显振荡;然后,由于降落伞的稳定作用,攻角α的振荡迅速衰减,逐渐趋于稳定,不难发现,投弹速度越大,攻角振荡越小。
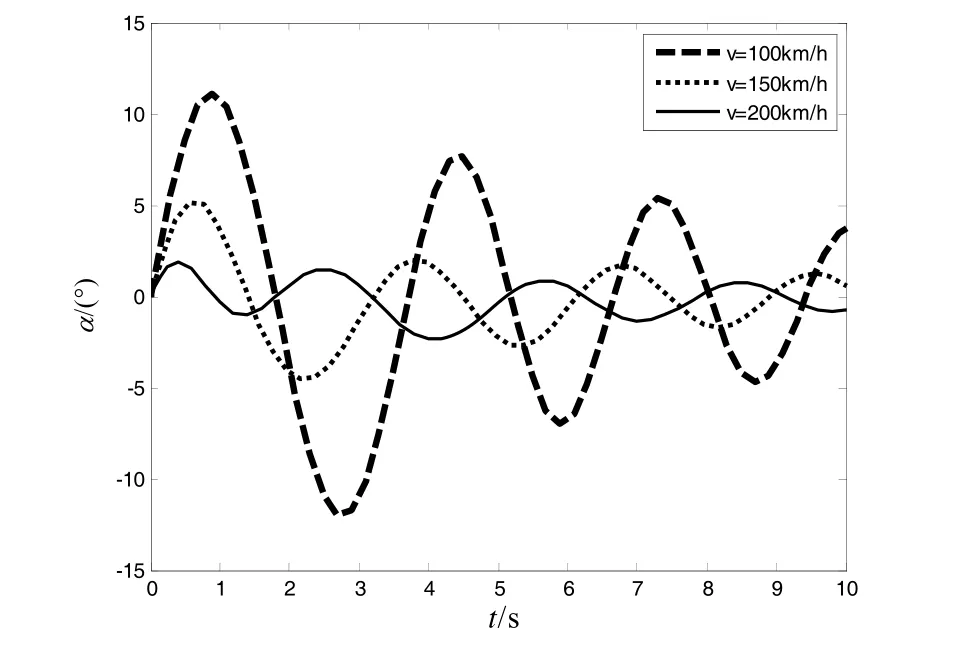
图7 投弹速度对攻角的影响
4.3 投弹速度、高度对深弹入水时间(即深弹滞空时间)的影响
图8给出了投弹速度分别为100 km/h、200 km/m、300 km/h时不同投弹高度投放深弹对深弹入水时间的影响变化曲线。结果表明,投弹高度越大,深弹滞空时间越长;同一高度投弹,投弹速度对入水时间影响较小;由水平轰炸原理知,滞空时间越长,受风等因素影响越大,引起的水平散布越大。

图8 投弹速度高度对深弹入水时间的影响
4.4 投弹高度对入水角的影响
图9给出了投弹速度为200 km/h时投弹高度对入水角影响的变化曲线,由图可知,投弹高度对入水角的影响较为明显,在一定范围内,入水角随投弹高度的增加而增大,趋于90°。

图9 投弹高度对入水角的影响
5 结论
通过以上分析,可以得出如下结论:
1)投弹参数(主要是投弹高度和投弹速度)对入水角的影响。
投弹高度对入水角的影响较为明显,在一定范围内增大投弹高度可增大入水角;投弹速度对入水角的影响很小。
2)投弹参数对入水时间的影响。
投弹高度越大,深弹滞空时间越长,受风等因素影响导致水平散布增大;投弹速度对深弹滞空时间影响较小。
3)深弹空中弹道的优化。
结合无动力自导深弹水下运动的特点,要保证深弹入水后快速稳定地向下运动,入水角应尽量趋于90°;为提高深弹命中概率,尽可能让深弹的入水点更精确,应尽量减小深弹滞空时间,降低深弹投放水平散布,这就要求深弹投放要合理选择投放速度和投放高度。
4)仿真结果表明,本文所建深弹空中弹道模型是合理正确的,仿真得出的深弹入水参数满足某型深弹入水要求,可为进一步研究深弹水下弹道及攻潜效能提供相关参考。
[1]杨福渠.火箭深弹射击效率[M].北京∶国防工业出版社,1992∶34-41.
[2]孙明太.反潜直升机使用航空深弹对潜攻击效果分析[J].水中兵器,1998(1)∶152-160.
[3]姜选凯,赵学涛,贾跃.航空自导深弹攻潜命中概率分析[J].火力与指挥控制,2009,34(8)∶64-67.
[4]贾跃,宋保维,李文哲.火箭深弹拦截鱼雷理论与方法研究[J].系统工程理论与实践,2005,26(4)∶137-140.
[5]林贤杰,贾跃,赵学涛,等.航空自导深弹攻潜效能模型与仿真[J].弹箭与制导学报,2008,28(4)∶131-134.
[6]孙明太.航空反潜战术[M].北京∶军事科学出版社,2003∶153-159.
[7]张宇文.鱼雷弹道与弹道设计[M].西安∶西北工业大学出版社,1999∶255-259.
[8]刘卫国.Matlab 程序设计与应用[M].2 版.北京∶高等教育出版社,2006∶265-277.
[9]韩子鹏.弹箭外弹道学[M].北京∶北京理工大学出版社,2008∶23-51.
