新型遥感图像增强技术
2011-03-24周立佳钱智博徐冠雷
周立佳,钱智博,徐冠雷
(1.西北工业大学航海学院,西安 710072;2.大连舰艇学院军事海洋系,辽宁 大连 116018)
1 概述
随着EMD 理论和应用研究的发展[1-2],二维EMD(Bidimensional EMDsition,BEMD)受到了越来越多的关注[3-14]。
单向二维经验模式分解(SDEMD)将二维图像以行或列展开为一维信号[3-5],用一维算法对二维图像进行处理,它在雷达信号粒子噪声消除中得到了应用,忽视了二维图像的相邻像素的关联性,它不是严格意义上的二维经验模式分解。文献[6-7]等给出的经验模式同属一类(IFEMD),它采用径向基函数提取包络的二维经验模式分解,其计算量以及存储量开销很大。上述算法还存在一个共性问题,即由于图像灰度值的剧烈变化会造成内蕴模式函数分量包含过亮和过暗的区域,称之为灰度斑,其原因是分解过程中没有对频率、最大时宽、最大空间宽度进行限制,而且包络插值由于过冲和欠冲对于剧烈变化的部分会产生过大震荡,表现为灰度斑。限邻域经验模式分解NLEMD[8,14]可以精细分解图像的各种层次信息,消除了灰度斑现象,并通过在高动态HDR(High Dynamic Range)图像压缩、图像融合、图像增强等方面的应用,证明该算法的有效性。还有,针对结构性极强的图像,传统定义的极值点无法描述图像的结构特征,导致图像包络不能体现局部均值,分解后的分量特征遭到破坏。针对这一缺陷,通过对图像的结构特征进行分析,结构经验模式分解SBEMD(Structure based BEMD)可以有效地提取分量的结构特征[9]。另外,当图像缺乏必要的极值点或者没有极值点时,所有的经验模式(包括NLEMD和SBEMD)几乎全部失效。而且,上述BEMD都存在二维模式混叠、边界效应、不同插值函数产生不同结果等问题。徐等人提出了基于噪声辅助的方法解决了这些问题[12-15]。但是,噪声辅助的方法存在着速度慢不利于实时处理以及无法调整分量带宽的缺陷。
为了改进这两个缺点,徐等人又提出了带限BEMD[16]。不过,带限BEMD 不具备方向选择性,因此,本文提出了各向异性BEMD(ANBEMD),不仅具备带限功能,同时具有方向选择性。下面,先给出传统二维EMD的算法[6-7]。
对于图像f (x,y),传统二维EMD算法如下。
1)初始化:r (x,y)=f(x,y)。
2)确定r (x,y)的极值点,包括极大和极小值。
3)采用二维插值函数求取上下包络:Edw(x,y)和Eup(x,y)。
4)计算上下包络的均值:
Men(x,y)=(Edw(x,y)+Eup(x,y))2。
5)将r (x,y)减去 Men(x,y):Mod (x,y)=r(x,y)−Men(x,y)。
6)若 Mod (x,y)不满足IMF,则r(x,y)=Mod(x,y),转到步骤1)。
7)得到IMF:imf (x,y)=Mod(x,y)。
8) r(x,y)=r(x,y)−imf(x,y)。
9)重复步骤1)~8),直到剩余量r (x,y)满足停止条件,如分解层数等。
通过步骤1)~9)的筛选过程,可得

本文将讨论改进的BEMD,其中插值函数采用三角几何插值函数。
2 各向异性BEMD
2.1 辅助信号构造
由于极值点密度是频率大小的直接反映,也就是说,高频信号对应为高密度极值点,低频信号对应为低密度极值点。因此,我们可以通过极值点的疏密来控制构造的辅助信号fa(x,y)的带宽。而这个极值点的疏密可以通过要分解图像f(x,y)(尺寸M×N像素)的极值点获取。辅助信号可以定义为

有

式中:
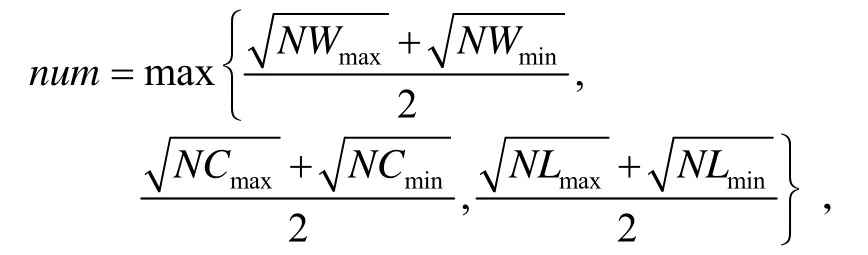
其中,NWmax为二维极大值点的数目;NWmin为二维极小值点的数目;NCmax是一维列极大值点的数目;NCmin是一维列极小值点的数目;NLmax是一维行极大值点的数目;NLmin是一维行极小值点的数目。[9]
s1、s2是用来调节辅助信号fa(x,y)的频率的常数,通常,s1,s2∈ [0.5,2]。
2.2 方向性选择
1)对原始待分解图像进行Fourier变换,获取其能量频谱函数;
2)对能量频谱函数进行Hough变换[17];
3)在Hough变换图中点按照从小到达排列,只留下前thd个点;
4)对上述做过处理的Hough变换图thd个点进行横坐标方向读取,即为原始待分解图像的主要及格方向信息。
由BEMD的特性可知,把几个获取的方向的垂直方向作为构造的辅助图像的方向即可。
2.3 算法流程
3)用传统BEMD分解fa+(x,y):
4)从待分解图像f(x,y)中减去fa(x,y):
5)用传统BEMD分解fa−(x,y):
6)求平均:

7)如果 res(x,y)不是剩余量,那么令f (x,y)=res(x,y)并转到步骤1),否则

显然,这种分解方法是一种带限滤波的过程,同时在二维中还具有方向选择性。
2.3.2 各向异性BEMD的实验分析
本部分,我们将采用各向异性BEMD 对lena进行分解实验,验证其有效性。从结果中可以看出,各向异性BEMD 不仅具有带限功能,同时还具备一定的方向选择能力。
各向异性BEMD方法具有更大的灵活性,只要有效地调整极值点密度和方向,便可以获取任意我们想要的带宽和方向分量信号。
另外,各向异性BEMD方法只是使用了两次辅助分量,分解速度相对于ASBEMD 极大地提高,和带限BEMD[3,16]具有类似的速度,即对于同样的分解,时间消耗只有ASBEMD的1/100~1/20。本文方法分解效果见图1。
2.3.1 各向异性BEMD的算法流程
1)由f(x,y)极值点构建辅助信号fa(x,y);
2)将fa(x,y)加到待分解图像上f(x,y):

图1 本文方法分解效果
3 多波段遥感图像融合
我们将应用各向异性BEMD 对多波段遥感图像进行融合。融合结果将和传统小波[15]融合算法、基于ASBEMD[12-13]的融合算法以及带限BEMD[16]进行比对。
对不同波段的待融合图像f1(x,y)和f2(x,y),融合算法定义如下。
1)用BLBEMD 对 f1(x,y)进行分解:
2)用BLBEMD 对 f2(x,y)进行分解:
3)基于如下规则进行融合:
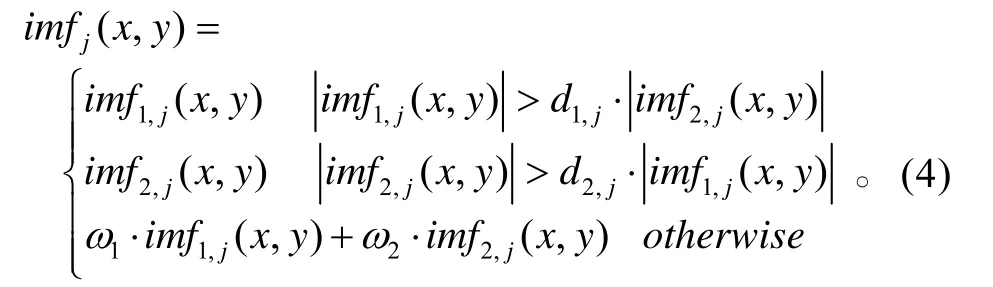
式4中:d12d、为门限值,ω1、ω2为权值满足和
4)融合剩余量:

5)重建融合后的图像:
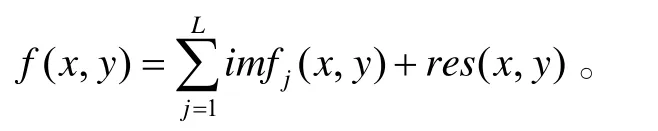
实验中,在和传统小波[15]融合算法以及基于ASBEMD[12-13]的融合算法进行比对的过程中,为实现比对的公平性,基于ASBEMD的融合算法的融合规则和本文是一致的。传统小波[15]融合算法的融合规则采用文献[14]中的方法。图2给出了融合的结果比对。显然,各向异性BEMD算法具有更好的融合效果。

图2 遥感图像融合比对
4 结论
本文提出一种基于方向辅助信号和所需带宽各向异性BEMD算法并用于遥感图像融合增强中。各向异性BEMD算法把给定的方向辅助信号和其对应负信号加到原始信号中去,构建两个待分解信号。再应用传统BEMD 把两个待分解信号进行分解,获取的分量相加得到对应的IMFs,辅助信号同时在相加的过程中被移除,各向异性BEMD算法有效地避免了边界效应和模式混叠。各向异性BEMD算法不仅速度快,而且具有方向选择功能和带宽控制效果。最终,遥感图像的融合证明了各向异性BEMD算法的有效性。
[1]HUANG N E,SHEN Z,LONG S R,et al.The empirical mode decompositionand the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proc.R.Soc.Lond.A,1998,454∶903-995.
[2]RILLING G,FLANDRIN P.One or two frequencies?The empirical mode decomposition answers[J].IEEE Trans.Signal Proc.,2008,56(1)∶85-95.
[3]HAN C,WANG G H,FAN C D.A novel method to reduce speckle in SAR images[J].International Journal of Remote Sensing,2002,23(23)∶5095-5101.
[4]YUE H Y,GUO H D,HAN C M,et al.A SAR interferogram filter based on the empirical mode decompositin method[J].Geoscience and Remote Sensing Symposium,2001,5∶2061-2063.
[5]LIU Z X,WANG H J,PENG S L.Texture segmentation using directional empirical mode decomposition[C]//Proceedings of the 17th International Conference on Pattern Recognition.2004∶279-282.
[6]NUNES J C,NIANG O,BOUAOUNE Y,et al.Texture analysis based on the bidimensional empirical mode decomposition with gray-level co-occurrence models[J].Machine Vision and Application,2003,2∶633-635.
[7]YANG Z H,QI D X,YANG L H.Signal period analysis based on Hilbert-Huang transform and its application to texture analysis[C]//Proceedings of the Third International Conference on Image and Graphics.2004∶430-433.
[8]XU G L,WANG X T,XU X G.Neighborhood limited empirical mode decomposition and application in image processing[C]//Fourth International Conference on Image and Graphics.Chengdu of China,2007∶149-154.
[9]XU G L,WANG X T,XU X G.Improved bi-dimensional EMD and Hilbert spectrum for the analysis of textures[J].Pattern Recognition,2009,42(5)∶718-734.
[10]PIELLA GEMMA.A general framework for multiresolution image fusion∶from pixels to regions[J].Information Fusion,2003,12(4)∶259-280.
[11]PHOL C.Multisensor image fusion in remote sensing∶concepts,methods and applications[J].International Journal of Remote Sensing,1998,9(5)∶823-854.
[12]XU G L,WANG X T,XU X G.Improved bidimensional empirical mode decomposition based on 2D assisted signals∶analysis and application[J].IET Image Processing,2011,5(3)∶205-221.
[13]WU Z H,HUANG N E,CHEN X Y.The multidimensional ensemble empirical mode decomposition method[J].Advances in Adaptive Data Analysis,2009,1(3)∶339-372.
[14]XU G L,WANG X T,XU X G,ZHU T.Multi-band image fusion algorithm based on neighborhood limited empirical mode decomposition[J].Journal of Infrared and Millimeter Waves,2006,25(3)∶225-228.
[15]ZHOU J,CIVCO D L.A wavelet transform method to merge Lansat TM and SPOT panchoromatic data[J].International Journal of Remote Sensing,1998,19(4)∶743-757
[16]ZHOU LIJIA,QIAN ZHIBO,XU GUANLEI.Band limited BEMD and Application in Remote Sensing Image Fusion[C]//The International Conference on Remote Sensing,Environment and Transportation Engineering.Nanjing,China,2011.
[17]GONZALEZ C R,WOODS E R.Digital image processing[M].2nd ed.Pearson Education,2003.
