同时到达捷变频雷达信号的DOA估计

刘鲁涛，司锡才，王立国

(哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001)

在高技术条件下的现代战争中，被动制导系统必须能在各种干扰背景下对雷达目标进行正确的捕捉与跟踪.而现代雷达为提高自身工作性能和抗干扰能力和躲避被动侦测系统的跟踪，在电子战双方夺取制电磁权，采取的主要技术措施包括扩展雷达工作频域范围、频率捷变、频率分集、超宽带等等，并配备雷达诱饵.针对雷达技术的变化，跟踪多个新体制雷达目标，使得传统的比幅/比相等被动侦测技术难以应付，因此对被动制导系统提出更高的要求.基于阵列信号处理的空间谱估计技术更多的应用在被动制导系统当中，用以跟踪多部雷达信号［1］.但传统的谱估计方法，如MUSIC［2］等等，要求多目标信号工作频率一致，并通过角度搜索估计目标方向.而对于同时到达目标信号工作频率不同的情况，传统谱估计算法的角度搜索不再适用.只能采用波达方向-频率联合估计的参数估计方法.如文献［3-4］是基于状态空间实现并结合ESPRIT方法，将波达方向-频率二维参数估计问题转化为2个一维参数估计.文献［5］基于PM(propagator method)对相关矩阵进行降维处理，给出波达方向-频率估计进而得出侦测目标方向.上述算法的局限性在于算法都是以ESPRIT为基础，要求特定的阵列结构且相对谱峰搜索技术精度较低;而且对于处理脉冲间捷变频的信号来讲，相邻脉冲频率跳变使信号子空间不停变化，需要在各个信号脉冲内重复的对信号波达方向－频率进行估计，工作量巨大，工程难以实现.文章提出了一种跟踪多部捷变频雷达目标的算法，其基本思想将多个捷变频雷达信号，映射成为单一参考频率的信号，从而构造一个对应单一频率的组合信号子空间，采用空间谱峰搜索的方法，得到多部捷变频雷达信号的方向估计.

1 信号模型

假设D个远场窄带信号入射到由M个阵元构成的天线阵(M＞D).在信号源不相关情况下，设阵列接收数据为x(t)，第i个阵元的接收数据为

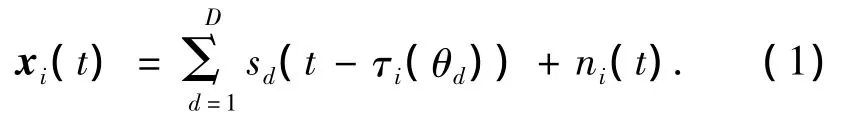
式中:ni(t)为第i个天线接收噪声;假定各阵元的噪声是均值为零的平稳空间白噪声过程，方差为σ2，并且噪声之间不相关，且与信号不相关;sd表示第d个目标信号;θd表示第d个信号源的到达角(DOA);τi(θd)相对于参考阵元，第d个信源传播到第i个阵元的延迟时间.在均匀线阵情况下，相邻阵元间的距离为l，τi(θd)=(i－1)lsin θd/c(c为波的传播速度).

如果信号源是窄带信号，可以将信号时间延迟近似等效为信号相位延迟，则信号可以写成:

M个阵元在特定时刻接收的信号可以写成:

式中:x(t)=［x1(t)x2(t)… xM(t)］T为M维的接收数据矢量，s(t)=［s1(t) s2(t) …sD(t)］T为D维信号矢量，A=A(Ω，F)=［a(θ1，f1) a(θ2，f2)…a(θD，fD)］为M×D维的阵列流型矩阵，a(θd，fd)=［1 e－j2πfdτ1(θd)… e－j2πfdτM－1(θd)］T为M维的导向矢量，Ω=［θ1θ2…θD］目标信号到达角集合，F=［f1f2… fD］为目标信号频率集合，n(t)=［n1(t)n2(t) … nM(t)］T为M维的噪声矢量.

捷变频雷达的瞬时工作频率在频率捷变带宽中的多个频率点随机跳动，其信号的特点是相邻2个发射脉冲的载频在一个很大的范围内以很高的速度跃变，也就是说在相邻脉冲内雷达信号的载频是不相等的.如图1(a)和(b)为第d部雷达信号脉冲间频率跳变时域和频谱示意图.捷变频雷达原理性能见文献［6，10］.从式(2)、(3)可以看出由于不同脉冲间每部雷达信号频率fd的跳变，导致每部雷达信号对应导向矢量a(θd，fd)在不同的脉冲间也是不断变化的.假设阵列观测时间足够长，采样数据来自K个回波脉冲，每个脉冲包含J个采样点(每个脉冲采样点数).第k(k=1，2，…，K)个脉冲内的采样数据:

这里S=［s1s2… sD］T为D×J维信号矩阵，不同脉冲采样数据Xk(M×J维)对应的不同的阵列流型Ak.所以简单组合所有采样数据进行测向不能实现.而对于文献［3-5］等波达方向—频率参数联合估计的方法，需要在各个脉冲间重复使用，工作量巨大;而且由于每个脉冲内采样数目J有限，难以达到满意的测向精度.

图1 捷变频雷达信号时频域示意图Fig.1 Scheme of radar signal of frequency agility

2 参考频率子空间估计及算法描述

2.1 参考频率子空间估计

引理 在一定条件下M×D维矩阵A(Ω，F)有rank［A(Ω，F)］=D，则一定存在一个非奇异的M× M维变换矩阵T(F)，使得

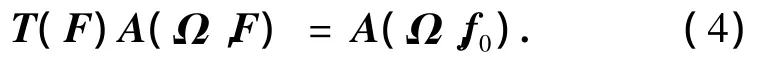
式中:A(Ω，f0)为M×D矩阵.

证明 因为A(Ω，F)和A(Ω，f0)都是秩为D的M×D维矩阵，则存在M×(M－D)维矩阵B(F)和B(f0)，使得M×M维矩阵［A(Ω，F)|B(F))］和［A(Ω，f0)|B(f0)］是非奇异阵.

T(F)的一个明显的选择为

这里变换矩阵T(F)不是唯一的.通常情况下可以选择B(f0)=BT(F)=［0D×(M－D)|IM－D］，这样选择的好处可以减少计算复杂度.通过分块矩阵的逆变换公式，把M×M维矩阵的逆变换转化为D× D维矩阵的逆变换的问题.可以得到变换矩阵:

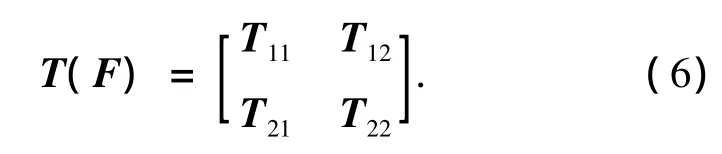
式中:

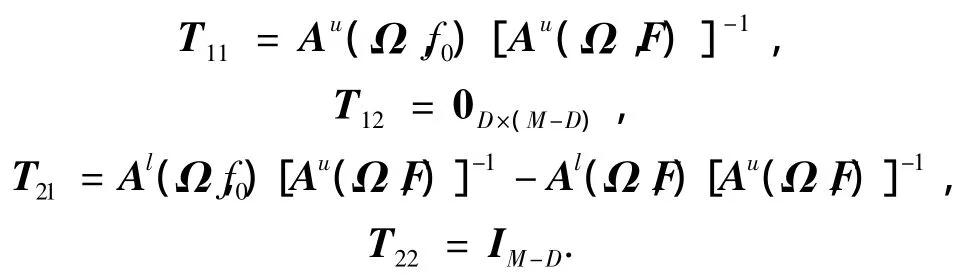
其中，Al和Au分别为矩阵A的上侧D×D维块阵和下侧的(M－D)×D维块阵.

使用变换矩阵T可以将不同频率观测矩阵变化成同一频率的观测矩阵，第k个采样脉冲内的观测数据矩阵变换为

则由式(4)和(7)可以将采样协方差矩阵变为

式中:

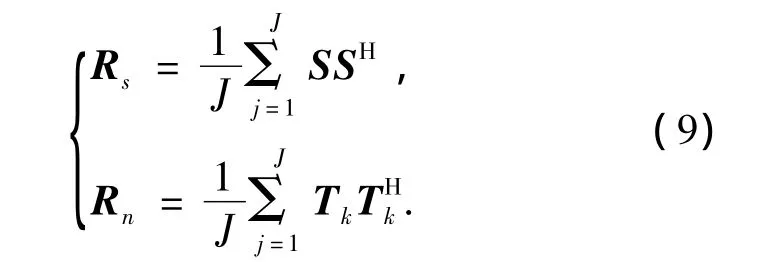
以上变换将导向矢量阵A(Ω，F)变为A(Ω，f0)，重新构造了信号子空间，使得不同的脉冲内的采样数据都对应相同的频率f0，通过这个方法使Rk(k=1，2，…，K)中的跳频信号能量都聚集参考频率f0内，并对应的信号子空间A(Ω，f0)内，因此可以对所有脉冲内的采样数据组合在一起，进行组合子空间测向处理.从而改善了对多个捷变频信号方向的估计性能.但是也产生了一个问题，这种变换可能使白噪声产生变化，改变输出信号处理的SNR.文献［7］分析了矩阵变换对白噪声矩阵的影响.

2.2 变换矩阵构造与算法描述

由式(5)可以看出，对于每个脉冲内数据的变换矩阵构造都需要求得该信号的频率和到达角度的预估计.对于雷达信号来讲，由于脉冲的间隔时间相对较短，目标信号的到达角在各个脉冲基本不变，则角度的预估计在任意一个快拍内完成即可(预估计的目标到达角度可以存在较大误差).而对与信号的频率是在不停的跳变的，所以对信号频率需要对每个快拍分别估计.

由此可以对第1个脉冲内的采样数据采用角度－频率联合估计［4，8］，得到信号的频率和角度预估计，构造T1.对于接下来的脉冲内数据只估计信号频率即可.通过观测数据的特征矢量对预估计的角度和频率进行参数配对.例如第k个脉冲的数据包括两部雷达信号，信号频率与角度的参数为f1、f2、θ1、θ2.则可能的信号阵列流行有以下2种可能:

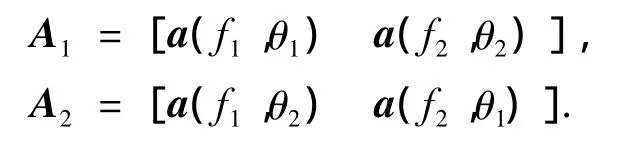
先求得第k个脉冲数据Xk的协方差阵，对其进行特征分解，得到信号和噪声的特征子空间Us和UN.由于信号流型与噪声的特征子空间UN正交，比较‖AH1UNUHNA1‖和‖AH2UNUHNA2‖大小，即可完成频率与角度参数配对，从而得到A(Ω，F).选定参考频率f0(参考频率选择在探测目标信号频率频段附近为宜)后，根据式(5)构造变换矩阵Tk.

算法实现步骤:

1)对第1个脉冲采样数据进行频率-角度预估计，使用文献［4，8］方法，得到第1个脉冲内各个信号的波达方向-频率预估计，作为初始值;

2)对余下不同脉冲的采样数据分别进行FFT或采用ESPRIT方法［9］，得到各脉冲内同时到达信号的频率估计;

3)频率-角度参数配对;

4)选定参考频率f0，构造各个脉冲内的数据变换矩阵Tk(F)，k=1，2，…，K;

5)通过式(7)形成变换后的观测数据Yk，使其阵列流行对应于同一频率f0，构造新的观测数据组合Y=［Y1Y2…YK］;

6)构造Y的协方差阵R，然后估计雷达目标波达方向(如使用MUSIC);

步骤4)～6)迭代可以改善估计性能.

3 计算复杂度分析

算法主要涉及的计算包括频率估计、协方差矩阵计算、特征值分解、变换矩阵构造以及谱峰搜索.步骤2)频率预估计需要的复数乘法数O(KJlbJ)，步骤3)中参数配对及步骤6)共K次特征分解需要O (M2DK)+O(M3K)次复数乘法;步骤4)K个变换矩阵构造见式(5)(6)，需要复数乘法数为O(D3K) +O(D2MK);步骤6)构造Yk需要O(M2JK)个复数乘法;构造协方差矩阵O(KJM(M+1)/2)复数乘法数;步骤7)采用MUSIC谱峰搜索得到目标到达角，假设采用线阵(一维搜索步长为1°，搜索范围［－ 90°，+ 90°］)需要的乘法数为O(181M(M－D)2).

由于M＞D，KJ＞J＞M.计算量主要集中在谱峰搜索和步骤5)的Yk构造.算法需要复数乘法数约为O(181M(M－D)2)+O(M2N)(N=JK为观测数据总的采样数).在实时处理系统中由于采样点数目有限，一般满足181M＞N时，计算量主要集中在谱峰搜索步骤.所以本算法与一般MUSIC算法计算量基本相同.同时相比于参数估计方法来讲，保证了谱峰搜索的高精度优点.

4 实验结果与分析

为了验证所提出算法的有效性及测向精度，对该算法进行计算机仿真试验.在下面仿真中，假设各向同性阵元数为M=8的的等距线阵.相邻阵元间距为d=c/2f'，f'信号可达到的最大频率.各个信号相互独立，阵列输入噪声为平稳零均值白高斯过程.采样频率符合奈奎斯特要求，观测脉冲数为K=4，每个脉冲内采样J=100.SNR定义为单个阵元信号能量与噪声能量的比值.

4.1 对2个捷变频信号的到达角估计

2信号来波方向分别为 θ=10°和 θ=30°，SNR=10 dB，2个信号载频在［500 MHz，600 MHz］任意跳变，参考频率选择为f0=600 MHz.图1给出了文中组合子空间算法2个信号到达角谱估计情况.由图可以看出该组合子空间算法可以正确估计出多个捷变频信号的DOA.

图2 组合子空间DOA估计(10次)Fig.2 DOA estimation of the combined subspace algorithm(10 times)

4.2 预估计对捷变频信号到达角估计性能影响

该方法在对付脉冲捷变频信号时，由于需要对某一个脉冲内的信号进行预估计(通常选择第一个到达脉冲)，所以有必要讨论预估计测向误差对该方法的测角性能进行讨论.

设2个信号来波方向分别为θ1=10°和θ2=30°， SNR=10 dB，2个信号载频在［500 MHz，600 MHz］任意跳变，参考频率选择为f=600 MHz.对预估计到达角分别为)θ1=7°和)θ2=27°、)θ1=5°和)θ2=25°以及)θ1=4°和)θ2=24°的3种情况该方法的测向准确性进行仿真.50次蒙特卡洛实验(如图3所示)结果表明在预估计偏离目标角度较大的情况，该方法可以较精确估计多部跳频信号的到达角.只要预估计误差在目标达到角(±5°)的波束范围内，该方法可以有效估计到达角;如果预估计偏差加大，会增大测向误差甚至测向错误.

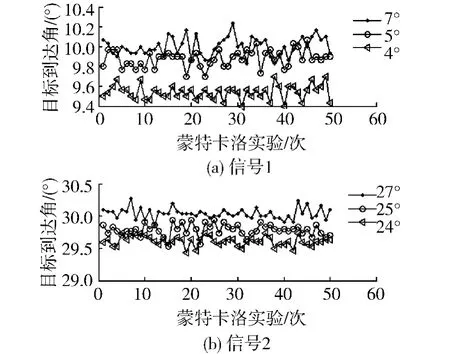
图3 预估计对测向方法的影响(50次)Fig.3 Performance of DOA estimation in different pre-estimation(50 times)

4.3 多捷变频信号到达角估计精度的统计分析

两信号来波方向分别为θ1=10°和θ2=30°，2个信号载频在［500MHz，600MHz］任意跳变，参考频率选择为f=600 MHz，谱峰搜索步进角度为0.1°.均方根误差RMSE(root mean squared error)随信噪比变化如图4所示.

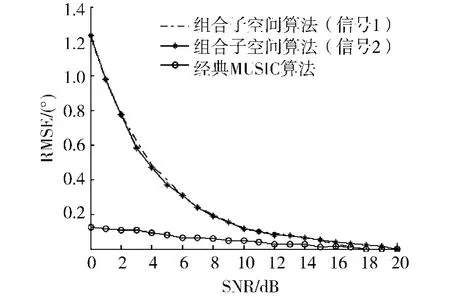
图4 DOA均方根误差随信噪比变化曲线Fig.4 RMSE of DOA estimation versus SNR

从图4可以看出信噪比较高情况下，该算法的均方根误差与经典MUSIC算法很接近，SNR在10 dB以上时基本保证0.1°以下，而SNR在0dB时也只有1°左右，符合被动测向精度要求.

5 结束语

基于阵列的目标波达方向估计都以估计导向矢量信息为基础.捷变频信号导向矢量随频率变化使得估计导向矢量变得困难.文章通过选择参考频率构造对应于同频率导向矢量，简化了导向矢量结构;利用同频导向矢量的组合信号子空间结构实现了多个捷变频信号的同时估计.相比于频率-DOA联合估计方法该方法在保证测向精度的同时，具有较小的计算复杂度适于实时处理的特点，适合于被动侦测系统对复杂雷达信号入射方向实现快速估计.

［1］谢机灵.超分辨测向算法在被动雷达导引头系统中的应用［D］.哈尔滨:哈尔滨工程大学，2008:78-91.

［2］SCHMIT R O.Multiple emitter location and signal parameter estimation［J］.IEEE Trans on AP，1986，34(3):276-280.

［3］LI F，VACCARO R.On frequency-wavenumber estimation by state-space realization［J］.IEEE Trans on CAS，1991，38(3):800-804.

［4］LEMMA A N.Joint angle-frequency estimation using multiresolution ESPRIT［C］//Proceedings of the 1998 IEEE International Conference on Acoustics，Speech and Signal Processing.Seattle，USA，1998:1957-1960.

［5］吴云韬，廖桂生，田孝华.一种波达方向—频率联合估计快速算法［J］.电波科学学报，2003，18(4):380-384.

WU Yuntao，LIAO Guisheng，TIAN Xiaohua.Fast algorithm for joint direction-of-arrival and frequency estimation［J］.Chinese Journal of Radio Science，2003，18(4):380-384.

［6］茅以海.频率捷变雷达［M］.北京:国防工业出版社，1981:27-31.

［7］HUNG H，KAVEH M.Focusing matrix for coherent signalsubspace processing［J］.IEEE Trans Accost，Speech，Signal Processing，1988(36):1272-1281.

［8］黄可生，黄知涛，周一宇.信号频率和DOA联合估计方法［J］.电子对抗，2003，6(6):1-4.

HUANG Kesheng，HUANG Zhitao，ZHOU Yiyu.An estimation method of the frequency and DOA of signals［J］.E-lectronic Warfare，2003，6(6):1-4.

［9］ZOLTOWSKI M D，MATHEWS C P.Real-time frequency and 2-D angle estimation with sub-Nyquist spatio-temporal sampling［J］.IEEE Trans Signals Processing，1994，42: 2781-2794.

［10］侯宝林，李陟，宋才水.捷变频雷达信号频域侦察截获技术研究［J］.现代防御技术，2007，35(1):87-91.

HOU Baolin，LI Zhi，SONG Caishui.Study on frequencydomain intercept technique for frequency agility radar［J］.Modern Defence Technology，2007，35(1):87-91.