Isotherm Equation Study of F Adsorbed from Water Solution by Fe2(SO4)3-modified Granular Activated Alumina*

DANG Dan (党丹), DING Wenming (丁文明),**, CHENG Anguo (程安国), LIU Shuming(刘书明) and ZHANG Xu (张旭) College of Chemical Engineering, Beijing University of Chemical Technology, Beijing 0009, China

2 School of Environment, Tsinghua University, Beijing 100084, China

1 INTRODUCTION

Several types of adsorbents have been studied for fluoride removal from the drinking water system [1-8].Granular activated alumina (GAA) appears to be the best applicable adsorbent [9-12]. GAA has a very high internal surface area, which provides many active sites for adsorption. However, the main disadvantage of commercially available GAA is its poor sorption kinetics because of the intraparticle diffusion limit of the solute and the low affinity of the solid surface to fluorine anions. The surface of activated alumina was usually modified by an active metal salt solution to enhance adsorption efficacy [13-15]. Our previous study[16] proved that GAA impregnated with Fe2(SO4)3solution has high fluoride adsorption capacity and better adsorption speed. The current paper will focus on the isotherm equation of F adsorbed on Fe2(SO4)3-modified GAA.

The isotherm equation displays the relationship between adsorption capacity and solution concentration,and is usually expressed in the Langmuir or Freundlich form, depending on the experimental data at a specific experimental condition. Each expression forms set definite assumptions and indicates a dominant adsorption mechanism. The study of the isotherm equation will not only determine the relationship between adsorption capacity and solution concentration, but also reveal the adsorption mechanism of the process.

The current study will be carried out to assess the adsorption equilibrium of a fluoride solution on 1-2 mm GAA modified by Fe2(SO4)3solution. A single Langmuir or Freundlich equation may not fit the entire concentration gap during equilibrium data processing. Thus, a new function, which is a combination of Langmuir and Freundlich, will be used to express the entire concentration gap.

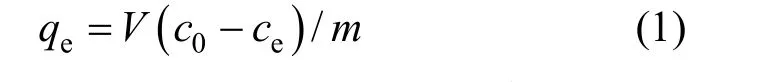
whereqeis the adsorption capacity (mg·g-1) at equilibrium,c0andceare the initial and equilibrium fluoride concentrations (mg·L-1), respectively,Vis the volume (L) of the solution, andmis the mass (g) of the adsorbent used.

The Langmuir and Freundlich adsorption isotherms were used to analyze the results. These isotherms are useful in describing the adsorption behavior of adsorbents.

2 MATERIALS AND METHODS

The adsorbent used was GAA modified with Fe2(SO4)3solution (MGAA) according to Dang [16].All chemicals used were analytical grade. All experiments were carried out at normal atmosphere. Stock fluoride solution was prepared by dissolving an appropriate quantity of sodium fluoride into deionized water. Bulk solution was used for the adsorption equilibrium experiments after appropriate dilution. The adsorption experiments were carried out in 250 ml plastic flasks with a 100 ml fluoride solution. After adding the adsorbent into the fluoride solution, the flasks were kept in a constant temperature rotator. The solution was filtered once sorption equilibrium was reached. The filtrate was collected and diluted with deionized water and was then analyzed for residual fluoride concentration using a fluoride ion-selective electrode. The relative error of measurement is less than 2%. The adsorption capacity at equilibrium (qe)was calculated from the following equation:

Table 1 Adsorption equilibrium models used in the present study

The Langmuir equation, Eq. (2), is the most commonly observed isotherm for chemical adsorption because of chemical adsorption strictly limited to the monolayer regime [17]. Its initial assumptions are that the solid adsorbent has limited adsorption capacity(qm), all active sites are identical, and one active site can only combine with one solute molecule (monolayer adsorption) [18]. The Langmuir isotherm is a simple application of the mass action law leading to the thermodynamic equilibrium constant. This links the concentration of free sites on the adsorbent with the adsorbate concentration in the solution and the concentration of complexed sites at the adsorbent surface. On the other hand, the simple and empirical Freundlich equation, Eq. (3), is the most important and commonly used isotherm equation for describing multilayer adsorption [19]. It has no saturated adsorption value and it is widely applied in physical and chemical adsorptions, as well as in solution adsorption. The Freundlich equation was applied in many cases, particularly in the case of a multilayer adsorption with possible interactions between adsorbed molecules [17]. The nonlinear and linear forms of the Langmuir and Freundlich equations are presented in Table 1. The Langmuir and Freundlich equations were applied on all experimental data.

3 RESULTS AND DISCUSSION

3.1 Initial experimental data

Isotherm experiments were carried out using initial fluoride concentrations (c0) ranging from 0.5 to 180 mg·L-1in deionized water (pH ～7.0). The adsorbent dose of the sorbent was 1.0 g·L-1, and the bottles were kept in the constant temperature rotator at 180 r·min-1and (25±1) °C for 48 h. Fig. 1 shows the results obtained by isotherm plottingqeversuscefor the isotherm experiments.

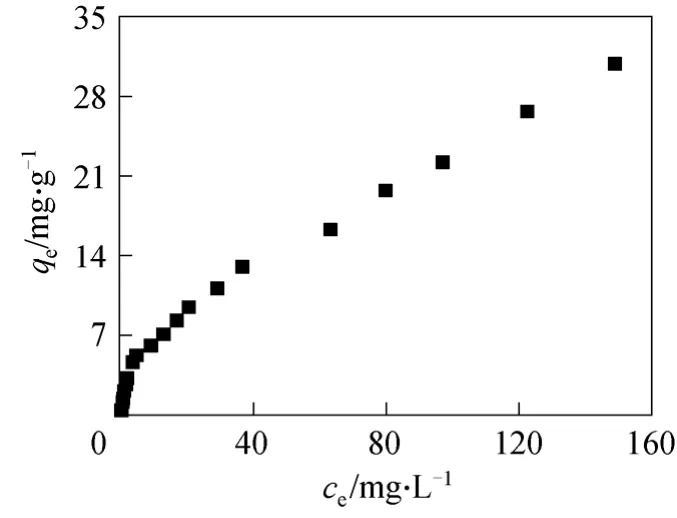
Figure 1 Fluoride adsorption isotherm in water (pH ～7.0)on MGAA (c0=0.5-180 mg·L-1, adsorbent dose=1.0 g·L-1)■ 0.1 mg·L-1＜ce＜150 mg·L-1

Figure 1 shows thatcerapidly increases linearly withqein low equilibrium concentrations (0.1 to 5.0 mg·L-1), and the slope ofqe/ceis about 1.0. Thecealso increases linearly withqein high equilibrium concentrations (5.0 to 150 mg·L-1). However, the rate of increase is obviously lower and the slope ofqe/ceis about 0.2, as estimatedkcain gas-solid fluidized bed risers.

3.2 Analysis of isotherm equations applied to all experimental data

The linear forms of the Langmuir and Freundlich equations [Eqs. (4) and (5)] were applied to all isotherm curve data in the current study. From the variance in Figs. 2 and 3 and Table 2, the linear form of the Langmuir equation clearly fits the experimental data well in low equilibrium concentrations (0.1 to 5.0 mg·L-1), but not in high equilibrium concentrations(5.0 to 150 mg·L-1). On the other hand, the linear form of the Freundlich equation fit the data well, both in low and high equilibrium concentrations, but a demarcation point between low and high equilibrium concentrations existed (Fig. 2). The obtained parameter values are presented in Table 2.

Figure 2 Application of the Langmuir model (linear form)for fluoride adsorption in water (pH ～7.0) on MGAA(c0=0.5-180 mg·L-1, adsorbent dose=1.0 g·L-1)■ 0.1 mg·L-1＜ce＜5.0 mg·L-1; ▲ 5.0 mg·L-1＜ce＜150 mg·L-1;—— Langmuir

3.3 Analysis of isotherm equations applied to low and high fluoride concentrations

Langmuir and Freundlich models were used to fit the experimental data for low and high concentrations,respectively, because a single model cannot fit all experimental data. The Langmuir and Freundlich constants are shown in Table 2. Figs. 4 and 5 show that the experimental data at low concentrations agreed well with both the Langmuir and the Freundlich models, and the values of the correlation coefficientR2were both 0.999 (shown in Table 2). On the other hand,the experimental data at high concentrations fit well with the Freundlich model, but not with the Langmuir model (Figs. 6 and 7).

Table 2 Comparison of equilibrium constants for low and high concentrations

Figure 3 Application of the Freundlich model (linear form) for fluoride adsorption in water (pH ～7.0) on MGAA(c0=0.5-180 mg·L-1, adsorbent dose=1.0 g·L-1)■ 0.1 mg·L-1＜ce＜5.0 mg·L-1; ▲ 5.0 mg·L-1＜ce＜150 mg·L-1;—— Freundlich

Figure 4 Application of the Langmuir model for fluoride adsorption in water (pH ～7.0) on MGAA (c0=0.5-10 mg·L-1, adsorbent dose=1.0 g·L-1)■ 0.5 mg·L-1＜ce＜5.0 mg·L-1; —— Langmuir

Figure 5 Application of the Freundlich model for fluoride adsorption in water (pH ～7.0) on MGAA (c0=0.5-10 mg·L-1, adsorbent dose = 1.0 g·L-1)■ 0.5 mg·L-1＜ce＜5.0 mg·L-1; —— Freundlich

In the analysis of the Langmuir and Freundlich equations applied to the experimental data, one possible interpretation is that there are two types of active sites at the surface of MGAA, as follows.

(1) The highly active sites, called L-type sites,are weakly present at the MGAA surface. Adsorption takes place prior at L-type sites in the first stage. Similar to the Langmuir assumptions, one L-type site can only combine with one fluoride ion and this adsorption process is monolayer adsorption. A single layer of fluoride ions is held to the adsorbent surface via chemical bonds [20]. The adsorption process predominantly takes place in L-type sites in low solution concentration. This means that at low concentrations the adsorption process is based on chemical adsorption.

Figure 6 Application of the Langmuir model for fluoride adsorption in water (pH ～7.0) on MGAA (c0=10-180 mg·L-1, adsorbent dose = 1.0 g·L-1)▲ 5.0 mg·L-1＜ce＜150 mg·L-1; —— Langmuir

Figure 7 Application of the Freundlich model for fluoride adsorption in water (pH ～7.0) on MGAA (c0=10-180 mg·L-1, adsorbent dose = 1.0 g·L-1)▲ 5.0 mg·L-1＜ce＜150 mg·L-1; —— Freundlich

Figure 8 Application of the Langmuir-Freundlich model for fluoride adsorption in water (pH ～7.0) on MGAA(c0=0.5-180 mg·L-1, adsorbent dose = 1.0 g·L-1)■ 0.1 mg·L-1＜ce＜150 mg·L-1; —— Langmuir-Freundlich

(2) The less active sites, called F-type sites, are strongly present at the MGAA surface. In high solutions concentration, after the L-type sites are saturated by the fluoride ions in the first stage, adsorption can take place at F-type sites in the second stage. One F-type sites can combine with more than one fluoride ion in high concentrations. This adsorption process is multilayer adsorption and the adsorption process is based on physical adsorption. In this multilayer adsorption, the adsorbed ions are held to the adsorbent surfaceviathe weaker van der Waals forces.

At low concentrations, when fluoride ions occupy the L-type sites till the surface saturation is reached, no further adsorption can take place at L-type sites. This adsorption process is called monolayer adsorption. At high concentrations, after the L-type sites are saturated by fluoride ions, F-type sites are occupied by residual fluoride ions. This adsorption process is the multilayer adsorption and it can be described by the Freundlich model.

3.4 Analysis of the new isotherm equation applied to all experimental data

A single equation cannot fit all experimental data,thus a new equation is formed by combining the Langmuir and Freundlich models:

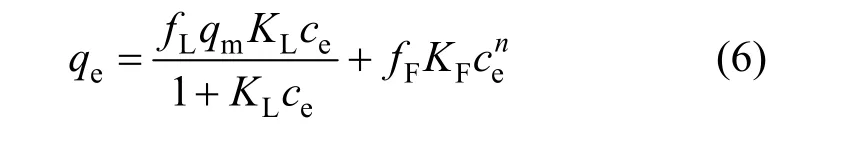
Figure 9 Application of the Langmuir-Freundlich model for fluoride adsorption in water (pH ～7.0) on MGAA(c0=0.5-10 mg·L-1, adsorbent dose = 1.0 g·L-1)■ 0.1 mg·L-1＜ce＜5.0 mg·L-1; —— Langmuir-Freundlich

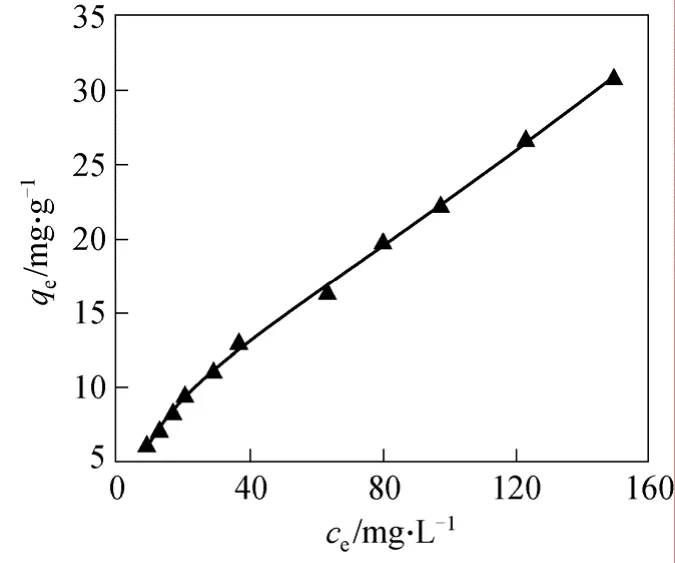
Figure 10 Application of the Langmuir-Freundlich model for fluoride adsorption in water (pH ～7.0) on MGAA (c0=10-180 mg·L-1, adsorbent dose = 1.0 g·L-1)▲ 5.0 mg·L-1＜ce＜150 mg·L-1; —— Langmuir-Freundlich

Table 3 Application of the Langmuir-Freundlich model:Equilibrium constants and other parameters

The new equation contains six parameters (qm,KL,KF,n,fL, andfF) and some uncertainties will be present when fitting data. It will be applied to the same set of experimental data. Thus, values were assigned to several parameters. Theqm,KL,KF, andnvalues of the nonlinear forms of the Langmuir and Freundlich equations in Table 2 were substituted to Eq.(3). The resulting equation was then fitted to all experimental data. The results werefL=0.15,fF=0.94,andR2=0.993.

The new equation considers the two adsorption mechanisms (monolayer and multilayer adsorptions)when fitting the data, and thus, it can be applied to the entire range of experimental data.

The valuesfL=0.15 andfF=0.94 were then substituted into the new equation, and the new equation was turned into a four-parameter one, which was then applied to the experimental data at low and high concentrations (R2were both 0.999). The new Langmuir-Freundlich equation can be used not only in the entire range of concentrations, but can also be applied at high and low concentrations. The new equation also considers the two different adsorption mechanisms when fitting the experimental data at low and high concentrations. This means that theR2of the new equation applied to the experimental data at low and high concentrations were greater than those using a single Langmuir or a single Freundlich equation.

4 CONCLUSIONS

The present study was carried out with a broad range of initial solute concentrations (0.5 to 180 mg·L-1).The application of two equilibrium models (nonlinear and linear forms) generally showed that a single Langmuir or Freundlich equation cannot fit the entire concentration gap. This indicates that fluoride adsorption probably occurredviatwo adsorption mechanisms. At very low adsorbent concentrations (0.5 to 5.0 mg·L-1),the fluoride adsorption process was probably based on chemical adsorption, whereas physical adsorption dominated in high concentrations (0.5 to 180 mg·L-1).

A new function, called the Langmuir-Freundlich equation, can be used not only in low and high concentrations, but also in the entire concentration range.The new equation considers the two adsorption mechanisms (monolayer and multilayer adsorptions)when fitting the data, and thus, it can be applied to the entire range of experimental data.

NOMENCLATURE

Cefluoride concentration at equilibrium, mg·L-1C0initial fluoride concentration, mg·L-1

KFFreundlich constant indicative of the relative adsorption capacity of the adsorbent, mg(1-n)·Ln·g-1

KLLangmuir equilibrium constant, L·mg-1

kcathe interphase exchange coefficient

mMGAA mass, g

nFreundlich constant indicative of the intensity of the adsorption

qeadsorption capacity at equilibrium, mg·g-1

qmmaximum adsorption capacity from Langmuir, mg·g-1

R2correlation coefficient

Vthe volume of fluoride solution, L

1 Raichur, A.M., Basu, M.J., “Adsorption of fluoride onto mixed rare earth oxides”,Sep.Purif.Technol., 24, 121-127 (2001).

2 Fan, X., Parker, D.J., Smith, M.D., “Adsorption kinetics of fluoride on low cost materials”,Water Res., 37, 4929-4937 (2003).

3 Cengeloglu, Y., Gar, E., Ersoz, M., “Removal of fluoride from aqueous solution by using red mud”,Sep.Purif.Technol., 28 (1), 81-86 (2002).

4 Wang, Y., Reardon, E.J., “Activation and regeneration of a soil sorbent for defluoridation of drinking water”,Appl.Geochem., 16,531-539 (2001).

5 Turner, B.D., Binning, P., Stipp, S.L.S., “Fluoride removal by calcite:Evidence for fluorite precipitation and surface adsorption”,Environ.Sci.Technol., 39, 9561-9568 (2005).

6 Vaaramaa, K., Lehto, J., “Removal of metals and anions from drinking water by ion exchange”,Desalination, 155, 157-170 (2003).

7 Amor, Z., Bariou, B., Mameri, N. , Toky, M., Nicolas, S., Elmidaoui,S., “Fluoride removal from brackish water by electrodialysis”,Desalination, 133, 215-223 (2001).

8 Ruiz, T., Persin, F., Hichour,M., Sandeaux, J., “Modelisation of fluoride removal in Donnan dialysis”,J.Membr.Sci., 212, 113-121(2003).

9 Ghorai, S., Pant, K.K., “Equilibrium, kinetics and breakthrough studies for adsorption of fluoride on activated alumina”.Separ,Purif.Technol., 42, 265-271 (2005).

10 Das, N., Pattanaik, P., Das, R., “Defluoridation of drinking water using activated titanium rich bauxite”,J.Colloid Interface Sci., 292,1-10 (2005).

11 Lounici, H., Addour, L., Belhocine, D., Grib, H., Nicolas, S., Bariou,N., Mameri, N., “Study of a new technique for fluoride removal from water”,Desalination, 114, 241-251 (1997).

12 Lee, D.R., Hargreaves, J.M., Badertocher, L., Rein, L., Kassir, F.,“Reverse osmosis and activated alumina water treatment plant for the California State prisons located near Blythe”,Desalination, 103,155-161 (1995).

13 Maliyekkal, S.M., Sharma, A.K., Philip, L., “Manganese-oxidecoated alumina: A promising sorbent for defluoridation of water”,Water research, 40, 3497-3506 (2006).

14 Tripathy, S.S., Bersillon, J.L., Gopal, K., “Removal of fluoride from drinking water by adsorption onto alum-impregnated activated alumina”,Separation and Purification Technology, 50, 310-317 (2006).

15 Maliyekkal, S.M., Shukla, S., Philip, L., “Enhanced fluoride removal from drinking water by magnesia-amended activated alumina granules”,Chem.Eng.J., 140, 183-192 (2008).

16 Dang, D., Ding, W.M., Huo, Y.K., “Fluoride removal by several modified granular activated alumina”,Journal of Beijing University of Chemical Technology(Natural Sciences), 37, 113-116 (2010).

17 Kolasinski, K.W., Surface Science: Foundations of Catalysis and Nanoscience, John Wiley and Sons, England 236 (2008).

18 Mardini, F. Al., Legube, B., “Effect of the adsorbate (Bromacil)equilibrium concentration in water on its adsorption on powdered activated carbon. Part 1. Equilibrium parameters”,Journal of Hazardous Materials, 170, 744-753 (2009).

19 Violante, A., Huang, P.M., Gadd, G.M., Biophysico-Chemical Processes of Heavy Metals and Metalloids in Soil Environments,Wiley-Interscience, America, 217 (2008).

20 Gowariker, V., Krishnamurthy, V.N., Gowariker, S., Dhanorkar, M.,Paranjape, K., Borlaug, N., The Fertilizer Encyclopedia, John Wiley and Sons, America, 15 (2009).