基于GPU的面向SPH流体模拟的邻居查找算法*

赵相坤 李凤霞 战守义

(北京理工大学北京市智能信息技术实验室，北京100081)

基于物理的模拟已广泛用于计算机图形学中，越来越多的自然现象如雨、泥浆、烟圈、海浪等都可以被逼真地模拟显示出来.这些模拟问题都可以归结为复杂的流体模拟.一个典型的流体模拟可以用Navie-Strokes方程表示:

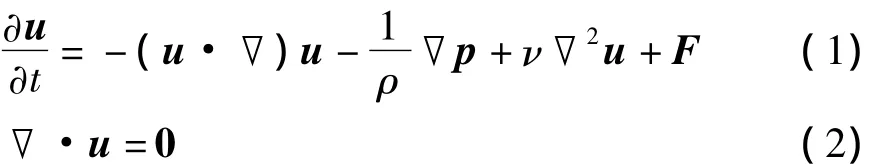
式中，u为流体速度，ρ为密度，p为压强，ν为动力粘滞系数，F为作用于流体的所有外力之和.

目前主要有两种跟踪流体移动的方法:(1)欧拉方法，该方法一般基于网格，在固定的网格点监测流体的参数(密度、速度、压强等)随时间的变化;(2)拉格朗日方法，该方法用一系列的粒子表示流体，流体在指定位置的参数通过对一定范围内粒子属性值的加权求和得到.

平滑粒子动力学(SPH)［1］是一种拉格朗日形式的流体模拟方法.在SPH方法中，流体用一系列的携带有各种流体属性的粒子表示，任意位置的流体属性通过对附近的粒子属性值进行加权求和得到.当使用的粒子数达到几十万甚至上百万时，查找指定位置的粒子的所有邻居就成为流体模拟的瓶颈.

为了查找粒子在指定位置处的邻居，一般采用空间划分的方法，将空间划分成均匀的网格，如图1所示.不同的粒子根据其位置属性分别属于不同的网格单元，位于同一网格内的粒子互为邻居，当然任一粒子的邻居还包括与粒子所在网格相邻的其余26个网格内的粒子.

图1 三维空间的网格剖分Fig.1 Grid partition in 3D space

为了实现粒子邻居的快速查找，已经有很多使用图形处理器(GPU)加速邻居查找的算法.Amada等［2］将GPU用于SPH的加速计算，但由于所使用的邻居查找算法是在CPU上实现的，每一次模拟都需要把邻居表从CPU传输到GPU，使得该方法无法充分使用GPU，CPU和GPU间的数据传输几乎抵消了后续的GPU计算方面的优势.文献［3］中将一种称为模板路由的数据结构用于最近邻居的查找，该方法需要预先建立一个复杂的纹理轨迹.由于任意空间网格用多个纹元表示，因此用于较大计算区域时需要一个大的纹理.Kipfer等［4］使用均匀的网格和排序方法在GPU上实现了粒子间的碰撞检测.Purcell等［5］使用基于排序的网格方法和模板缓冲来处理位于同一个单元内的多个光子.Harada等［6］提出了一种基于SPH的流体模拟系统，该系统使用桶纹理来表示3D的网格结构并实现了一种高效的邻居查找算法，但每一个网格内最多只能有4个粒子.Bayraktar等［7］提出了一种在GPU上实现的基于网格的邻居查找算法，复杂的纹理产生过程使得该算法虽然可在GPU上实现，但是速度低于同类基于排序网格的方法.

为此，文中提出了一种新的在GPU上实现的基于网格的邻居查找算法.首先使用粒子初始位置信息建立粒子的网格纹理图，然后对粒子的网格纹理按照粒子的网格id在GPU上排序，最后利用排序的网格纹理和原始的网格纹理在GPU上建立粒子的邻接纹理图，实现粒子邻居的快速查找.

1 算法原理及步骤

为了实现粒子邻居的快速查找，需要建立一张如图2所示的邻接纹理图:水平方向上保存了特定粒子的所有邻居，其中R存储当前粒子的索引号，G存储当前粒子的邻接粒子索引号，B未用，故用-1填充;在垂直方向上粒子按索引号依次排列.

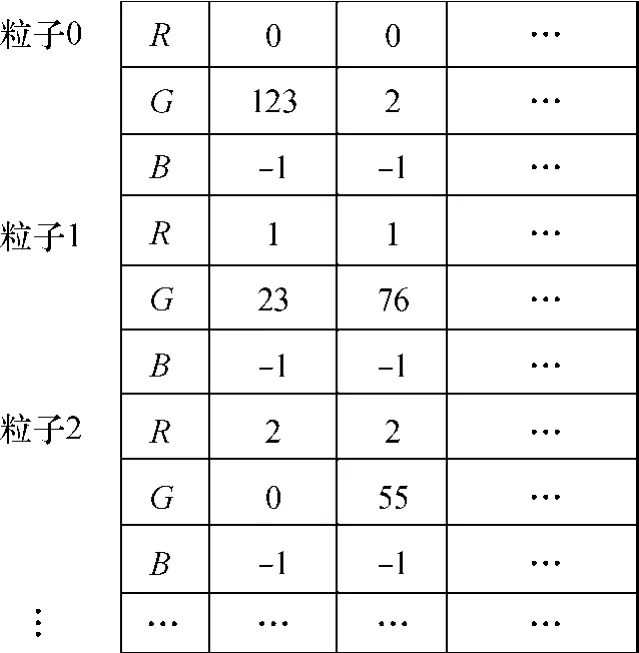
图2 邻接纹理图Fig.2 Neighbor texturemap

图3给出了基于GPU的邻居查找算法流程图，在开始时需要建立一张存储粒子位置信息的纹理图，用作网格纹理的输入，以后所有的操作全部在GPU上实现.按照邻居表的建立顺序，下面给出详细的实现方法.

图3 基于GPU的邻居查找算法流程图Fig.3 Flowchart of GPU-based neighbor search algorithm

1.1 建立粒子网格纹理图

初始时的粒子位置纹理如图4(a)所示，其中(xpos，ypos，zpos)为粒子的坐标，partIdx为粒子的索引号，A为纹理的透明位.为了能迅速地找到粒子的邻居，通常将包围流体的容器空间划分为三维的网格，任意粒子都属于某一个网格.

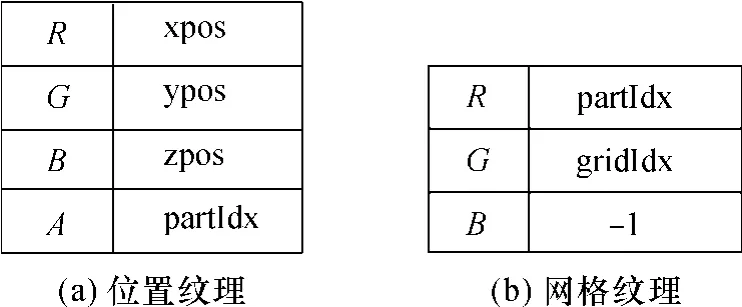
图4 粒子位置纹理和网格纹理Fig.4 Particle position texture and grid texture

为了得到粒子所属网格以及和所属网格直接相邻的其它网格，首先由粒子的位置信息计算出粒子的所属网格，即以粒子的坐标除以单元格的大小得到每个粒子的网格位置信息(ix，iy，iz).按照式(3)进行相应的转换:

式中:b、h和d分别为x，y，z3个方向上网格单元的宽度、高度和深度.按照

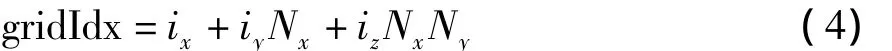
计算出粒子的一维网格id，其中Nx和Ny分别为水平和垂直方向上的网格总数.

将粒子所属容器的几何信息(位置和空间大小)以及粒子位置纹理图作为输入参数传递给像素着色器，就可以很容易地建立一张如图4(b)所示的粒子网格纹理图.位置纹理和网格纹理都是按照粒子的自然顺序排列的，即按照partIdx有序.

1.2 备份网格纹理图

初始的网格纹理图按照粒子的partIdx有序排列.为了快速查找位于同一网格内的所有粒子，可以使用基于GPU的折半查找算法［8］.使用基于GPU的查找算法需要网格纹理中的粒子按照gridIdx有序，而在建立粒子邻接纹理图时，需要借助原始的网格纹理图得到粒子的partIdx，为此在对网格纹理排序前需要事先备份网格纹理图.使用像素着色器可以将原来的网格纹理作为输入写入到备份纹理中.

1.3 排序网格纹理图

为了快速查找具有相同网格id的粒子，需要对网格纹理按照gridIdx进行排序.目前存在很多在GPU上实现的排序算法，如奇偶归并排序［8］、Bitonic归并排序［8］、改进的Bitonic归并排序［9］、GPUSort［10］、桶排序［6］、快速排序［11］等.文中采用奇偶归并排序方法，单步的奇偶归并排序GPU着色程序可以参考文献［8］.经过排序后，具有相同网格id的粒子相邻排列.

1.4 建立粒子邻接纹理图

图5给出了生成粒子邻接纹理图的过程，其中传输的数据标示在箭头头部，数字表示执行的先后顺序.

图5 邻接纹理图的生成过程Fig.5 Creation procedure of neighbor texturemap

图2中邻接纹理的R位的粒子索引从纹理坐标y计算得到.如果每张纹理图存储4096个粒子，那么纹理的R位保存的粒子索引号为

式中，P为页序号，介于0～Np/4096之间，Np为粒子总数.

在得到粒子索引号partIdx后，在备份的原始网格纹理图上得到该粒子的网格(文中称为直属网格)序号gridIdx，这样根据gridIdx，在排序后的网格纹理图中，使用基于GPU的折半查找算法［8］就可以得到与当前粒子网格id相同的其它粒子首次出现的位置.

在CPU上预先计算出相邻的27个网格id间的间隔，然后传输到GPU，叠加到当前粒子的grid Idx就可以得到任意粒子所属的其余26个网格.

虽然得到一个粒子的27个网格(直属网格及其26个相邻的邻居网格)内粒子首次出现的位置gridIdxStart，如何得到后续的相邻粒子以及得到后写入到纹理的什么位置是GPU邻居查找方法的关键.这是因为和CPU不同的是，在GPU上，像素着色器不允许将指定的值写到纹理的任意指定的位置上.为此，文中提出了一种解决像素着色器不能将任意值写入到纹理的指定位置的方法.

首先，假定任意粒子拥有相同数目的邻居并且任意网格都拥有相同数目的粒子，这样任意粒子都会在邻接纹理中出现27次，使用式(6)将纹理的横坐标x除以每一个网格内的最大粒子数Nmax，p，就得到该粒子所属的片段step Idx(介于0～26之间)，利用式(7)可以得到粒子在片段内的偏移量offset，将这个偏移量叠加到利用折半查找算法得到的首次出现的位置，就可以得到位于同一网格内的后续粒子的网格索引号.

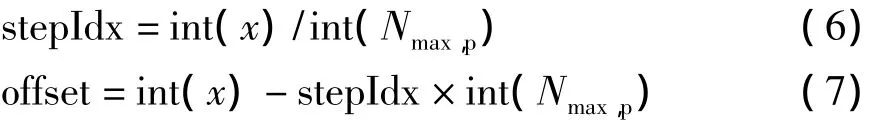
式中，int(·)为取整.

将网格索引号转化为纹理坐标，然后利用纹理坐标从已排序的网格纹理中的R位得到当前粒子(索引号为partIdx)的可能邻居粒子partIdxNeighbor.这些可能的邻居粒子在最终写入到纹理之前还要做如下的判别:

(1)如果partIdxNeighbor和partIdx相等，则说明找到的粒子和当前粒子是同一个粒子而不是邻居，否则就是潜在邻居;

(2)如果是潜在邻居，则求取两者之间的距离，如果该距离小于平滑半径则是邻居，否则不是邻居.

按照上面的思想，最终建立了一张如图2所示的粒子邻接纹理图.

2 文中算法与其它算法的比较

2.1 与基于CPU的邻居查找算法的比较

在CPU上可以采用二叉空间分割(BSP)树、多维树、三维网格等来实现邻居的查找.文中采用三维网格来实现基于CPU的邻居查找，该算法和文中提出的基于GPU的邻居查找算法的时间比较如图6所示.从图6可知:(1)基于GPU的邻居查找算法的性能明显优于基于CPU的邻居查找算法;(2)随着粒子规模的不断增加，基于CPU的邻居查找算法的查找时间迅速上升，而且其增幅要高于基于GPU的邻居查找算法，说明基于CPU的邻居查找算法更适用于小规模的邻居查找，在粒子越多的情况下，基于GPU的邻居查找算法性能的优越性越明显.

图6 2种算法建立邻接纹理图所用时间的比较Fig.6 Comparison of time cost for creating neighbor texture map by two algorithms

除了查找时间上的差异外，将文中提出的基于GPU的邻居查找算法应用于基于SPH的流体模拟，可以保证流体模拟完全运行在GPU上，从而解决了在CPU上建立邻接表，在CPU和GPU之间频繁传输数据的低效问题［2］.

2.2 与其它基于GPU的算法的比较

与目前两个主流的基于GPU的邻居查找算法——Bayraktar算法［7］和Harada算法［6］相比，文中算法主要做了如下改进:

(1)Bayraktar算法在生成网格纹理图时，需要统计网格纹理图中具有相同grid Idx的粒子总数和具有相同grid Idx的粒子首次出现的位置，并保存到纹理中，文中算法丢弃了这一步;

(2)同一网格内的粒子数通过改变邻接纹理图的宽度灵活设置，弥补了Harada算法只允许同一网格最多有4个粒子的局限，提高了计算精度.

3 应用实例

采用文中提出的基于GPU的邻居查找算法来实现完全基于GPU的SPH流体模拟，其流体模拟框架如图7所示.图8给出了文中算法使用6万个粒子进行模拟时粒子在容器内的波动效果，表1给出了在NVIDIA 9600显卡上文中算法和Bayraktar算法于不同粒子数下的帧速率对比.从表1可知，在NVIDIA 9600显卡上，文中算法可以获得11.6 f/s的帧速率，而Bayraktar算法在同样的硬件条件下只能达到2.8 f/s的帧速率，说明文中算法因在GPU邻接纹理图生成过程方面的改进而大大提高了模拟的帧速率.从表1还可以知道，文中算法的模拟速度大约是Bayraktar算法的3～4倍.

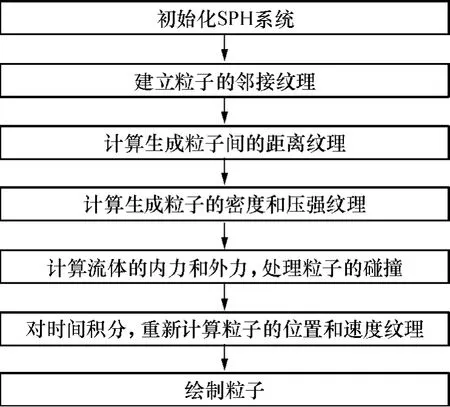
图7 基于GPU的SPH流体模拟框架Fig.7 Framework of GPU-based SPH fluid simulation

图8 使用文中算法模拟6万个粒子在容器内的波动效果Fig.8 Waving simulation results in a poolwith 6×104 particles using the proposed algorithm

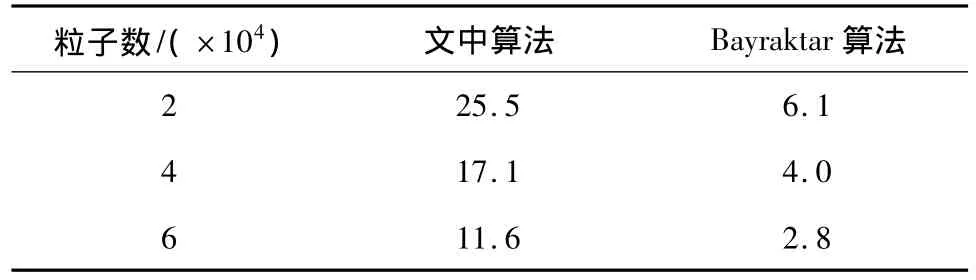
表1 不同粒子数下两种算法的帧速率Table 1 Frame-rates of two algorithmswith differentnumbers of particles

在同样的硬件条件下，使用文中算法与Harada算法［6］进行了对比实验.如果每个网格内的最大粒子数只能是4，那么在粒子特别多时，位于一个网格内的粒子往往超过4个，就会出现因没有将粒子纳入邻接纹理图而导致粒子逃逸容器的情况;增加网格剖分的粒度，可以不受最多只有4个粒子的限制，但会降低模拟的速度.因此文中提出的控制粒子邻居的方法更加灵活.

图9是一组将一个球丢入容器内时使用6万个粒子模拟的情况，流体的自由表面采用文献［12］中算法构建.由于文献［12］中算法运行于CPU上，在GPU上产生的粒子位置信息不得不从纹理中读回CPU中，因此模拟的速度大大降低，在NVIDIA 9600显卡和Intel Core2 Duo CPU E4400硬件条件下，可以得到2.3 f/s的帧速率，这和Harada算法［6］在同样条件下的帧速率相当.

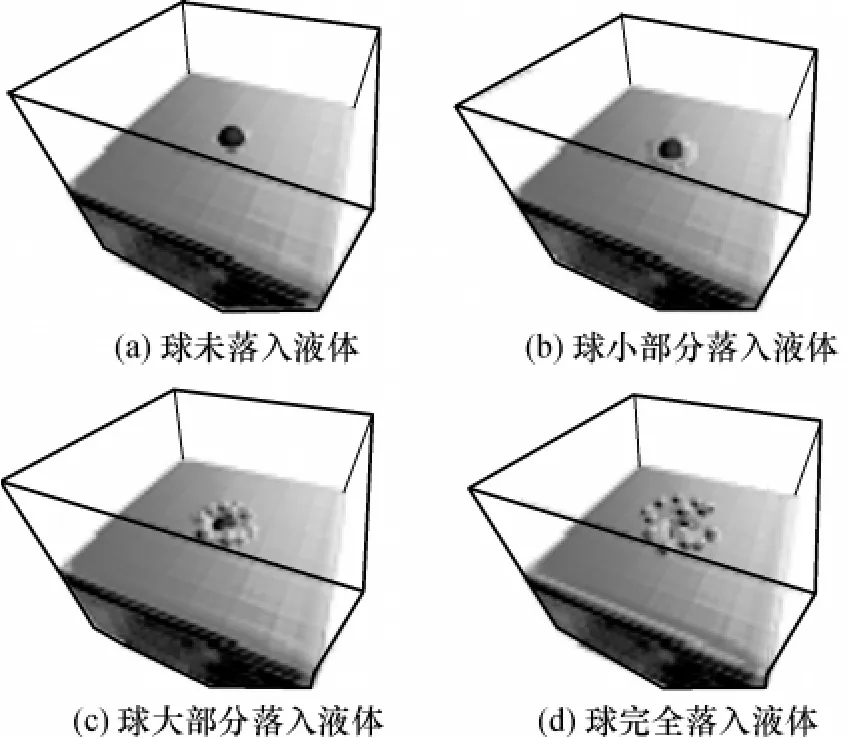
图9 使用6万个粒子模拟的球丢入容器内的效果Fig.9 Simulation results of throwing a ball into a tank with 6×104 particles

4 结语

文中提出了一种新的基于GPU的适合SPH流体模拟的邻居查找算法，该算法保证了SPH方法可以完全运行于GPU上，大大改进了传统方法在CPU实现邻居查找时的CPU和GPU间数据传输的低效问题.实验表明，和其它基于GPU的邻居查找算法相比，文中算法不但查找速度提高了3～4倍，而且邻居粒子数最大值灵活可控，保证了算法的精度.

文中算法将邻居粒子索引号写入纹理位置，克服了GPU无法将指定数据写入纹理任意位置的缺点，大大改进了GPU算法的性能.同样，这种基于GPU的邻居查找算法也适合于其它基于粒子的应用.但文中算法使用了大量的纹理缓存，在一定程度上降低了算法的效率.

［1］Müller M，Charypar D，Gross M.Particle-based fluid simulation for interactive applications［C］∥Proceedings of ACM SIGGRAPH/Eurographics Symposium on Computer Animation.San Diego:ACM，2003:154-159.

［2］Amada T，Imura M，Yasumuro Y，et al.Particle-based fluid simulation on GPU［C］∥Proceedings of ACM Workshop on General-Purpose Computing on Graphics Processors.Los Angeles:ACM，2004:1-2.

［3］Müller M，Solenthaler B，Keiser R，et al.Particle based fluid-fluid interaction［C］∥Proceedings of ACM SIGGRAPH/Eurographics Symposium on Computer Animation.Los Angeles:ACM，2005:237-244.

［4］Kipfer P，Segal M，Westermann R.Uberflow:a GPU based particle engine［C］∥Proceedings of ACM SIGGRAPH/Eurographics Conference on Graphics Hardware.New York:ACM，2004:115-122.

［5］Purcell T J，Donner C，Cammarano M，et al.Photon mapping on programmable graphics hardware［C］∥Proceedings of ACM SIGGRAPH/Eurographics Conference on Graphics Hardware.San Diego:ACM，2003:41-50.

［6］Harada T，Koshizuka S，Kawaguchi Y.Smoothed particle hydrodynamics on GPUs［C］∥Proceedings of Computer Graphics International.Berlin/Heidelberg:Springer-Verlag，2007:63-70.

［7］Bayraktar S，Güdükbay U，Özgüc B.GPU-based neighborsearch algorithm for particle simulations［J］.Journal of Graphics，GPU，and Game Tools，2007，14(1):31-42.

［8］Fernando Randima.GPU gems:programming techniques，tips and tricks for real-time graphics［M］.Boston:Addison-Wesley，2004:107-121.

［9］Pharr Matt，Fernando Randima.GPU gems2:programming techniques for high-performance graphics and general-purpose computation［M］.Boston:Addison-Wesley，2005:733-746.

［10］Govindaraju N K，Manocha D，Raghuvanshi N，et al.GPUSort:high performance sorting using graphics processors［R］.North Carolina:Department of Computer Science，University of North Carolina at Chapel Hill，2006.

［11］Cederman D，Tsigas P.A practical quick sort algorithm for graphics processors［R］.Göteborg:Department of Computer Science and Engineering，Chalmers University of Technology，2008.

［12］Lorensen W E，Cline H E.Marching cubes:a high resolution 3D surface construction algorithm［C］∥Proceedings of the 14th Annual Conference on Computer Graphics and Interactive Techniques.New York:ACM，1987:163-169.