基于线图Q-谱的点模式匹配算法*

朱明梁栋†唐俊范益政颜普

(1.安徽大学电子信息工程学院，安徽合肥230039;2.安徽大学计算智能与信号处理教育部重点实验室，安徽合肥230039;3.安徽大学数学科学学院，安徽合肥230039)

点模式匹配是计算机视觉和模式识别领域中的一个重要问题，其主要任务是寻找出相关点集之间的匹配关系，在立体视觉匹配、图像配准、目标识别与跟踪等方面有着广泛的应用.近年来，谱图理论［1］作为一种有效的数学工具被引入到点模式匹配问题的研究中，并发挥了重要作用.文献［2］中最早将谱方法应用于点模式匹配，即通过构造图像之间点的亲近矩阵，并对此矩阵进行奇异值分解(SVD)来获得对应关系.该方法可以处理不同大小点集的匹配问题，但对较大角度的旋转效果较差.文献［3］中采用了图像内部点的亲近矩阵来进行匹配，可以处理旋转问题，但对不同大小点集的匹配效果较差.文献［3］中方法实际上是对赋权图的邻接矩阵进行处理，王年等［4］从赋权图的矩阵表示入手，用赋权图的Laplacian矩阵来表示点集中点之间的关系，通过Laplacian谱来完成点集的匹配.为了进一步提高谱方法的性能，人们还使用了一些优化算法.Carcassoni等［5］将谱方法和EM(Expectation Maximization)算法结合起来，通过点的亲近矩阵来获得点匹配的概率，进一步提高算法对点集大小和位置噪声的鲁棒性;Tang等［6］将薄板样条(TPS)变形模型用于提高Laplacian谱方法的匹配效果.

上述谱方法均侧重于强调特征向量的作用，利用特征向量来求解点的匹配，忽略了特征值之间的相似性，虽然文献［5］中将特征值作为权值加入到匹配概率的求解过程中，但没有起到主要的作用.利用特征向量来解决匹配问题的优点是构造简单、计算量小，缺点是当点集的大小不同时，很难获得较好的匹配效果，这主要是因为特征向量对图结构特别敏感，当点集大小不同时，所构造的图结构差异较大，大大降低了特征向量间的相似性，导致匹配结果不理想.

目前，谱图理论的研究主要集中在图的特征值方面［7-10］，应用代数和组合的理论，建立图的特征值和一些不变量之间的联系.例如，图的Laplacian矩阵的零特征值的重数等于该图的连通分支数，Laplacian矩阵的次小特征值又称为图的代数连通度，若代数连通度大于0，则图是连通的;反之，则图是不连通的.在图的矩阵表示中，矩阵的全体特征值称为图的谱，具有相同谱但不同构的图称为同谱图.有关同谱图的研究［11］也是谱图理论的一个重要方面，它将特征值作为相应图的数字特征，考虑一个图能否由其特征值所唯一确定，目的是将图的结构信息通过图谱反映出来.图的无符号Laplacian矩阵的研究是近期的一个热点［11-14］，文献［11］中指出，由于无符号Laplacian矩阵较其它矩阵(邻接矩阵、Laplacian矩阵)的同谱图少，因此无符号Laplacian矩阵的谱(简称Q-谱)能够更好地反映图的结构信息，更便于研究图的性质.

文中利用Q-谱(即无符号Laplacian矩阵的全体特征值)来表示点的特征，通过这些特征计算点之间的匹配概率(相似性)，最后通过KM(Kuhn-Munkres)算法［15］来寻找点集之间的最优匹配以完成匹配，其中为了获得每个点的Q-谱表示，对每个点定义了大小一致的线图，对线图的无符号Laplacian矩阵进行谱分解，利用分解所得的特征值来表示点的特征.

1 基本概念

图是一个有序对(V，E)，V是顶点集，E是边集，当集合元素个数有限时，(V，E)称为有限图，否则称为无限图.不含平行边和自回路的图称为简单图.每对顶点都有边相连的简单图，称为完全图.对于一个完全图，若对其每条边赋以一定的值(如边的长度)，则称此图为赋权完全图.

若顶点vi与vj由一条边相连，则称vi与vj邻接.设G是一个含有n个顶点(v1，v2，…，vn)的图，则图G的赋权邻接矩阵A(G)的元素定义为

在无向图G=(V，E)中，对边集E的任一子集M⊆E，如果M中任意两条边都不关联，则称M为图G的一个匹配.G中属于M的边称为匹配边，匹配边的两个端点互为匹配点，所有匹配边的顶点称为关于M的饱和点，否则称为非饱和点.若G的每个顶点都是M的饱和点，则称M是G的完美匹配.若完美匹配M中边的权值之和是所有完美匹配中最大的，则称M为最优匹配.若G中存在一条路径R，路径的边是由属于M的匹配边和不属于M的非匹配边交替出现组成，且R的两个端点都是M的非饱和点，则称这条路径为可增广路.

2 线图的Q-谱

设I、J是两个相关点集，记I中的点为pi(i=1，2，…，m)，J中的点为qj(j=1，2，…，n)，不失一般性，设m≤n.

对点集I构造赋权完全图，对任意两点之间的边赋以该边的长度，如此可以得到一个阶数为m的赋权完全图.对于I中的点pi，有m-1条边与pi相连，分别记为e1≤e2≤…≤em-1(按长度排序)，则前k(2≤k≤m-1)条边e1，e2，…，ek与pi构成了一个星图Xi，求Xi的线图.由于e1，e2，…，ek中任意两条边都是关联的，因此，Xi的线图是一个k阶完全图Li，对Li构造赋权无符号Laplacian矩阵，其元素为

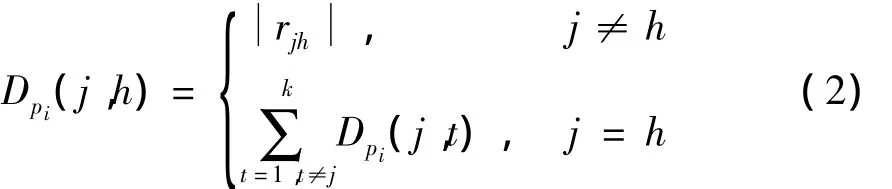
式中，rjh为ej与eh的长度差.

线图的求解过程就是将边变为点的过程，线图中的点是原图的边，点是邻接的当且仅当原图中对应的边是关联的.如图1(a)所示，e1、e2、e3为与pi关联的边，长分别为1、2、3，相应的线图(见图1(b))中，e1、e2、e3分别变为3个点，边的权分别为e1、e2、e3之间长度差的绝对值.

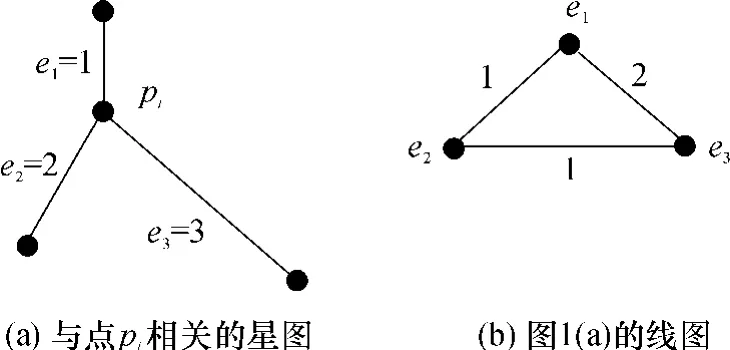
图1 线图的构造Fig.1 Construction of line graph

由于D pi是一个对称的半正定矩阵，因此对D pi进行谱分解，获得k个非负特征值λ1(pi)≥λ2(pi)≥…≥λk(pi)≥0，将(λ1(pi)，λ2(pi)，…，λk(pi))作为pi(i=1，2，…，m)的特征.

按照上述方法，对J中第j个点qj(j=1，2，…，n)选取与qj相关联的前k(2≤k≤m-1)个最短边来构造线图，同样可获得qj的特征表示

(θ1(qj)，θ2(qj)，…，θk(qj))，

其中θ1(qj)≥θ2(qj)≥…≥θk(qj)≥0.

构建匹配矩阵C，其第i(i=1，2，…，m)行第j(j=1，2，…，n)列的元素为

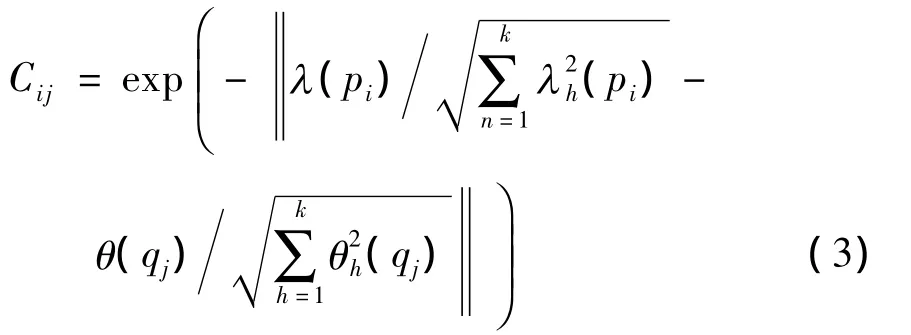
3 最优匹配

二分图的最优匹配是图论中的一个经典问题，它解决的一个典型应用问题如下:假设有n个员工、n项工作，每个员工都能胜任每项工作，但每个员工做每项工作的效率可能不同，并且每个员工最多只能从事一项工作，怎样给出一个安排方案使总效率最大?

将二分图的最优匹配应用到点模式匹配中，可以这样表述，点集I中的每个点与点集J中的每个点都有匹配概率，I中的点与J中的点必须是一一对应的，如何判断I与J之间点的匹配关系，才能使得总的匹配概率最大(即两个点集的相似度最大)?解决这个问题的经典有效算法是KM算法［15］.KM算法的具体步骤如下:

1)给出初始标号

b(pi)

3)若I中的所有点都是M的饱和点，则M是G的最优匹配，计算结束.

4)在I中找一非饱和点p0，令

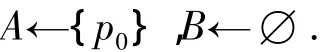
5)若NGb(A)=B，NGb(A)为与A中的点邻接的所有点构成的集合，则转步骤9).

6)找点q∈NGb(A)-B.

7)若q是M的饱和点，则找出q的配对点x，，转步骤5).

8)存在一条从p0到q的可增广路径R，令为环和运算，E(R)为R的边集，转步骤3).

4 基于线图Q-谱的点模式匹配

为了判断I与J之间点的匹配关系，定义I与J之间的相似度为

式中，Pi为I中第i点与J中所选定的匹配点之间的匹配概率.判断I与J中点之间匹配关系的准则是使得S(I，J)达到最大.在应用Q-谱方法获得两个点集中点之间的匹配概率后，以I、J为两个部分构造二分图，并在I部分中增加n-m个虚拟点，对二分图两部分之间的边赋以其所连接两点之间的匹配概率，I部分中n-m个虚拟点与J部分中点之间的边权赋以0.不难发现，使得S(I，J)最大的匹配关系即是所构造的二分图的最优匹配.

基于线图Q-谱的点模式匹配算法的基本思想是:先应用Q-谱方法获得两个点集间的匹配概率，然后构造二分图，最后应用KM算法寻找最优匹配.算法具体步骤如下:

1)为待匹配点集I和J分别构造赋权完全图GI和GJ;

2)根据GI和GJ，分别利用每个点的前k条最短边构造相应的线图;

3)为线图构造无符号Laplacian矩阵;

4)对无符号Laplacian矩阵进行谱分解，获得每个点的特征值表示;

5)根据式(3)计算匹配概率;

6)构造二分图，利用KM算法求解最优匹配，输出匹配结果.

5 实验及结果分析

为验证文中算法的性能，采用该算法与文献［3-5］中算法进行实验，其中文献［3，5］中算法的高斯平滑系数均选为σ=50.

5.1 模拟实验

模拟数据采用文献［16］中的合成数据，即由98个离散点构成的鱼图像，分别用文中算法和文献［3-5］中算法进行实验.当两个模拟数据大小一致时实验结果如图2(a)和表1所示.由表1可知，4种算法均有较高的匹配正确率，其中文献［3-4］中算法可以达到80%以上，结合了优化算法的文中算法和文献［5］中算法的匹配正确率更是达到了100%，这表明了谱方法与优化算法相结合的优势.

在两个模拟数据相差5个点的情况下，为了使得文献［3-5］中算法能够顺利进行匹配，先按照文献［5］中算法删除多出的向量及向量中的分量，实验结果如表1和图2(b)所示.从表1可知，应用特征向量来求解点匹配的文献［3-5］中算法，在点数不一致的情形下，匹配正确率下降较大，单纯的谱方法(如文献［3-4］中算法)几乎很难获得正确匹配点，而结合EM算法的文献［5］中算法虽然在匹配正确率方面有了较大的提升，但依然不太理想.文中算法的匹配正确率最高，说明文中算法能够处理大小不一致的点集匹配问题.对于点pi，选取与pi相关联的前k条最短边来构造线图，k的大小决定了pi的特征是全局性的还是局部性的:当k较小时，选取的是pi与其邻近点之间的边，pi的特征是局部特征;当k很大时，选取的边代表了pi与大部分点之间的关系，此时pi的特征倾向于全局性.一般情况下，在两个点集大小不一致时，多出的点大部分是一些边缘的噪声点，因此，利用点集所构造的图在局部上是很相似的，这是文中算法能够处理一些大小不一致的点集匹配问题的原因.

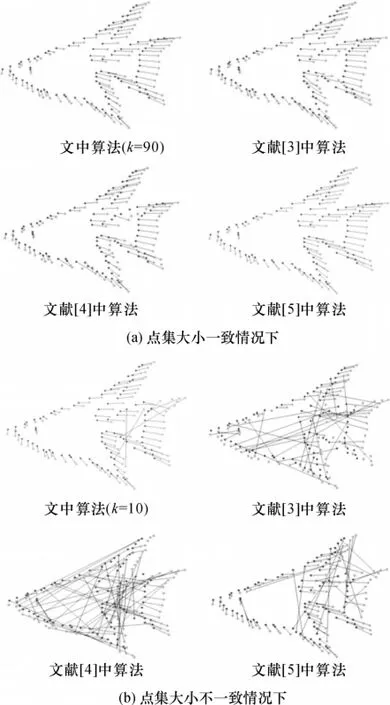
表1 几种算法对鱼图像的模拟结果比较Table 1 Comparison of simulated results of several algorithms for fish images

5.2 真实图像实验

文中通过大量的真实图像实验来验证所提算法的有效性，实验图像来自CMU/VASC图像数据库的图像序列，分别选取了第10、20、30、40、50、60帧图像，在每帧图像上选取30个点进行实验.在图像间帧数相差30、40、50的情况下几种算法的实验结果如表2和图3、4所示.从表2可知:当帧数差变大时，几种算法的匹配正确率均下降，单纯的谱方法(如文献［3-4］中算法)的匹配效果不如文献［5］中算法与文中算法;在两幅图像相差30帧的情况下，文中算法与文献［5］中算法均能获得完全正确的匹配结果;在两幅图像相差40帧的情况下，文献［5］中算法不能获得完全正确的匹配结果;当两幅图像的帧数差变为50时，文中算法的匹配正确率下降，但依然高于其它3种算法.

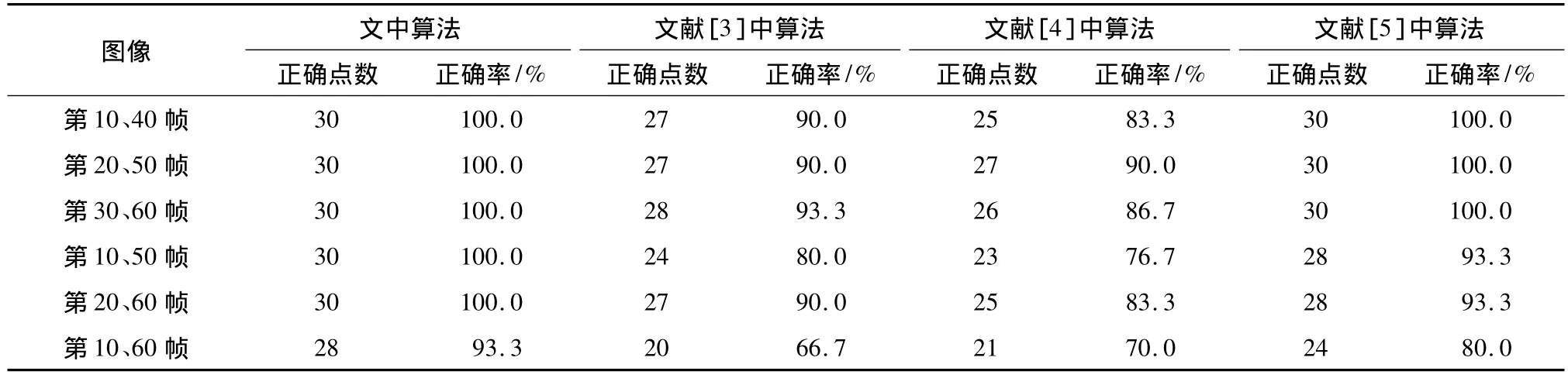
表2 几种算法对真实图像的实验结果比较Table 2 Comparison of experimental results of several algorithms for real images

图3 几种算法在图像帧数相差30情况下的匹配结果Fig.3 Matching results of several algorithms when the difference in frame number is 30

5.3 性能分析

首先分析文中算法的复杂度，由于Q-谱方法的复杂度主要集中在谱分解上，谱分解的复杂度为O(n3)，需要O(n)次谱分解，所以Q-谱方法的复杂度为O(n4)，KM算法的复杂度为O(n4)，所以文中算法的复杂度为O(n4).

另外，还可以对文中算法进行优化，降低计算复杂度.如在能够满足算法精度要求的情况下，构造线图时所选的边数k尽可能地小，谱分解的复杂度实际上为O(k3)，则Q-谱方法的复杂度为O(nk3);采用文献［17］中方法对KM算法进行优化，其复杂度降低为O(n3)，此时文中算法的复杂度降低为O(nk3+n3).

为验证文中算法在不同点数差下的稳定性，选取100个随机点进行实验，在按一定比例将点删除后，再与原点集进行匹配，同时使用文献［3-5］中算法进行对比实验，结果如图5所示.从图5可知，在两个点集的点数相差接近自身点数的50%时，文中算法依然能够获得90%以上的匹配正确率，但其它3种算法的匹配正确率下降较大，文献［5］中算法的效果要稍好于文献［3-4］中算法.

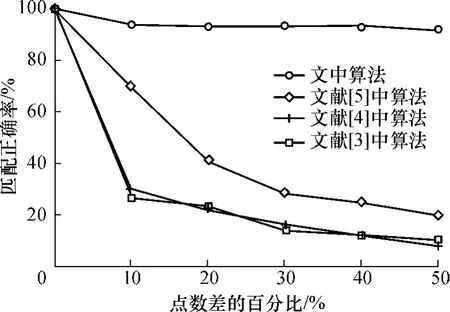
图5 几种算法在两个点集的点数相差一定比例下的性能比较Fig.5 Performance comparison of several algorithms when the point numbers of two point sets differ in a certain ratio

6 结语

针对大多数谱方法不能够较好地处理不同大小点集匹配的问题，文中提出了一种基于线图Q-谱的点模式匹配算法.该算法首先利用无符号Laplacian矩阵的谱来表示点的特征，然后通过这些特征计算点之间的匹配概率(相似性)，最后通过KM算法来寻找点集之间的最优匹配来完成匹配.实验结果表明，文中算法具有较高的匹配精度，可以处理不同大小的点集匹配问题.如何利用文中算法来处理一些更加复杂的图像匹配问题是今后研究的主要方向之一.

［1］Chung Fan R K.Spectral graph theory［M］.Providence:American Mathematical Society，1997.

［2］Scott G L，Longuet-Higgins H C.An algorithm for associating the features of 2 images［J］.Proceedings of the Royal Society London B:Biological Sciences，1991，244:21-26.

［3］Shapiro L S，Brady JM.Feature-based correspondence:an eigenvector approach［J］.Image Vision Computing，1992，10(5):283-288.

［4］王年，范益政，韦穗，等.基于图的Laplace谱的特征匹配［J］.中国图象图形学报，2006，11(3):332-336.Wang Nian，Fan Yi-zheng，Wei Sui，et al.Feature matching based on Laplace spectrum of graph［J］.Journal of Image and Graphics，2006，11(3):332-336.

［5］Carcassoni M，Hancock E R.Spectral correspondence for point pattern matching［J］.Pattern Recognition，2003，36(1):193-204.

［6］Tang J，Liang D，Wang N，et al.A Laplacian spectral method for stereo correspondence［J］.Pattern Recognition Letters，2007，28(12):1391-1399.

［7］Mohar B，Juvan Martin.Some applications of Laplace eigenvalues of graphs［M］∥Harn G，Sabiussi G.Graph symmetry:algebraic methods and applications.Dordrecht:Kluwer Academic Publishers，1997:227-275.

［8］Grone R，Merris R，Sunder V S.The Laplacian spectrum of a graph［J］.SIAM Journal Matrix Analysis Applications，1990，11(2):218-238.

［9］Merris R.Laplacian matrices of graphs:a survey［J］.Linear Algebra and Its Applications，1994，197/198:143-176.

［10］Oliveira C S，de Lima L S，de Abreu N M M，et al.Bounds on theQ-spread of a graph［J］.Linear Algebra and Its Applications，2010，432(9):2342-2351.

［11］Van Dam E R，Haemers W H.Which graphs are determined by their spectrum?［J］.Linear Algebra and Its Applications，2003，373:241-272.

［12］Cvetkovi'c D，Simi'c SK.Towards a spectral theory of graphs based on the signless Laplacian，I［J］.Publications De L’InstitutMathématiques，2009，85(99):19-33.

［13］Cvetkovi'c D，Simi'c SK.Towards a spectral theory of graphs based on the signless Laplacian，II［J］.Linear Algebra and Its Applications，2010，432(9):2257-2272.

［14］Cvetkovi'c D，Simi'c SK.Towards a spectral theory of graphs based on the signless Laplacian，III［J］.Applicable Analysis Discrete Mathematics，2010，4(1):156-166.

［15］肖位枢.图论及其算法［M］.北京:航空工业出版社，1993:134-142.

［16］Chui H，Rangarajan A.A new pointmatching algorithm for non-rigid registration［J］.Computer Vision and Image Understanding，2003，89(2):114-141.

［17］张超，曾显华，齐凯隆.基于二分图匹配的一类多机调度问题研究［J］.软件导刊，2009，8(7):73-75.Zhang Chao，Zeng Xian-hua，Qi Kai-long.Research of a class of scheduling problem ofmulticomputer based on bipartite graph matching［J］.Software Guide，2009，8(7):73-75.